Chapter 28 Binary Search
https://leetcode.com/tag/binary-search/
下面用到的术语:
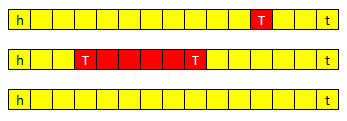
h表示head index,t表示tail index. T表示target.
Binary Search不但可以查找点,还可以查找范围.下面是几种情况.
- Optimization of binary search in Linux Kernel:
https://github.com/torvalds/linux/commit/166a0f780a8fdb67f232c85e9905ba84f7247da9?diff=split
Infinite Loop:
int _last_less(const vector<int> &v, int T) { // v:{1,2}, T: 12
int h = 0, t = v.size() - 1;
while (h < t) {
int m = h + (t - h) / 2;
if (v[m] < T)
h = m;
else
t = m - 1;
}
if (h < v.size() and v[h]<T)
return h;
return -1;
}475 Heaters 30.3% Easy
454 4Sum II 43.5% Medium
441 Arranging Coins 35.9% Easy
436 Find Right Interval 41.4% Medium
410 Split Array Largest Sum 32.6% Hard
392 Is Subsequence 44.2% Medium
378 Kth Smallest Element in a Sorted Matrix 43.4% Medium
374 Guess Number Higher or Lower 33.6% Easy
367 Valid Perfect Square 37.4% Medium
363 Max Sum of Rectangle No Larger Than K 32.2% Hard
354 Russian Doll Envelopes 31.8% Hard
350 Intersection of Two Arrays II 43.7% Easy
349 Intersection of Two Arrays 45.7% Easy
302 Smallest Rectangle Enclosing Black Pixels 44.0% Hard
300 Longest Increasing Subsequence 37.4% Medium
287 Find the Duplicate Number 41.8% Hard
278 First Bad Version 24.4% Easy
275 H-Index II 33.6% Medium
270 Closest Binary Search Tree Value 38.2% Easy
240 Search a 2D Matrix II 38.0% Medium
230 Kth Smallest Element in a BST 42.1% Medium
222 Count Complete Tree Nodes 27.0% Medium
209 Minimum Size Subarray Sum 28.7% Medium
174 Dungeon Game 22.9% Hard
167 Two Sum II - Input array is sorted 48.3% Medium
162 Find Peak Element 35.9% Medium
154 Find Minimum in Rotated Sorted Array II 36.2% Hard
153 Find Minimum in Rotated Sorted Array 38.7% Medium
81 Search in Rotated Sorted Array II 32.9% Medium
74 Search a 2D Matrix 35.6% Medium
69 Sqrt(x) 26.9% Medium
50 Pow(x, n) 27.0% Medium
35 Search Insert Position 39.0% Medium
34 Search for a Range 30.9% Medium
33 Search in Rotated Sorted Array 32.0% Hard
29 Divide Two Integers 15.9% Medium
4 Median of Two Sorted Arrays 20.8% Hard
不用begin和end的原因是为了和STL里面end表示past the last的语义区分开来. head和tail都是身体的一部分,从这个意义上也说得通.
每次拿中间点的值A[mid]去和目标值比较,并且根据结果缩小搜索范围.
head----------mid--------------tail
target可以在左边,右边或者等于A[mid].
看了下网上的总结都太麻烦.我现在总结一个最简单的.
- 永远用
while(h<=t)
- 永远用lower median, 即
m=l+(r-l)/2
- 永远用
h=m+1或者t=m-1.
先写:
然后来判定是否应该加等号.还有跳出等号之后该用h还是t.v[m]总是往T的方向走,如果T在左边,移动t,如果T在右边移动h.而且移动的时候永远是h=m+1或者t=m-1. 至于如果加等号,就看题目要求什么.
如果是求first element greater than T(target),如果v[m]==T,因为要找比T大的,所以应该往右边走/找,往右找意味着移动h,就是h=m+1.所以应该把等号添到上面的程序中. while loop之后我们要查看h还是t呢? h和t代表一个区别的起始和终止index,如果是求第一个元素就用h,最后一个元素就用t. 因此,我们在while结束之后只要查看h是否小于v.size(),如果小于,就是有效index,就是结果;否则返回-1,表示找不到.
如果是求first element greater or equal to T,如果v[m]==T,因为左边还可能有等于的点,这时候就应该往左走.往左走意味着移动t,就是t=m-1,所以上面的程序不需做任何改动.因为是求区间的第一个元素,while loop之后检查h即可.
用上面的方法可以轻易的推出下面的代码:
// find the first one in the feasible area
int _1st_equal(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] < T) h = m + 1;
else t = m - 1;
}
if (h < v.size() && v[h] == T) return h;
return -1;
}
int _1st_greater(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] <= T) h = m + 1;
else t = m - 1;
}
if (h < v.size()) return h;
return -1;
}
int _1st_equal_or_greater(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] < T) h = m + 1;
else t = m - 1;
}
if (h < v.size()) return h;
return -1;
}
// find the last one in the feasible area
int _last_equal(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] <= T) h = m + 1; else t = m - 1;
}
if (t < v.size() && v[t] == T) return t;
return -1;
}int _last_less(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] < T) h = m + 1; else t = m - 1; //等于的时候应用这个logic
}
if (t < v.size()) return t;
return -1;
}int _last_equal_or_less(const vector<int>& v, int T) {
int h = 0, t = v.size() - 1;
while (h <= t) {
int m = h + (t - h) / 2;
if (v[m] <= T) h = m + 1; else t = m - 1;
}
if (t < v.size()) return t;
return -1;
}二分法对应的数据结构本来是binary search tree, 所以循环里面走向就是两个.
这样的设计可以有效避免binary search的死循环.而且算法异常清晰.
28.1 278. First Bad Version
https://leetcode.com/problems/first-bad-version/
这个题可以翻译成找满足某一条件的区间的第一个元素的位置.这个条件就是isBadVersion()==true,根据上面的分析,当满足这个条件时,我们查找的范围应该向左移动,就是t=m-1;不满足向右,就是h=m+1. 于是可以马上写出这样的代码.
int firstBadVersion(int n) {
int h=1, t=n;
while(h<=t){
int m=h+(t-h)/2;
if(isBadVersion(m))
t=m-1;
else
h=m+1;
}
return (h<=n) ? h : -1;// 因为查找第一个元素,所以查看h,在范围内就返回h;否则-1
}这个模板每次h,t都移向可行域中的值,而且不能h和t都移动到m,这样的话会有infinite loop:
28.2 Basic - Search in Sorted Array
找到的话返回index,找不到返回-1.
网上看到这种方法:
int bsearch(vector<int>& nums, int target) {
int h=0, L=nums.size(), t=L-1;
while(h <= t){ // 1
int m = h+(t-h)/2; // 2. lower median
if(nums[m]<target) h=m+1; // 3
else if(nums[m]>target) t=m-1;
else return m;
}
return -1;
}我觉得这样其实更好(参见33. Search in Rotated Sorted Array)
28.3 367. Valid Perfect Square
https://leetcode.com/problems/valid-perfect-square/
struct Solution {
bool isPerfectSquare(int num){//edge case:1,808201 == 899*899
int l=0, r=(num+1)/2; // 1.num/2+1 is also ok
while(l<=r){
long long m = l+(r-l)/2; //2 int type is wrong
if(m*m == num) return true;
else if (m*m < num) l=m+1;
else r=m-1;
}
return false;
}
};这题套模板很简单,但是有两个值得注意的地方.
- r的初始值不能是num/2,不然输入是1的话会返回false
- m的类型不能是int,不然有int overflow
T: \(O(1)\) Solution:
https://discuss.leetcode.com/topic/49339/o-1-time-c-solution-inspired-by-q_rsqrt
- Template 2:
28.4 33. Search in Rotated Sorted Array
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand. (i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
Your algorithm’s runtime complexity must be in the order of O(log n).
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1https://leetcode.com/problems/search-in-rotated-sorted-array/
这道题是二分查找Search Insert Position的变体,看似有点麻烦,其实理清一下还是比较简单的.因为rotate的缘故,当我们切取一半的时候可能会出现误区,所以我们要做进一步的判断.具体来说,假设数组是A,每次左边缘为l,右边缘为r,还有中间位置是m.在每次迭代中,分三种情况:
(1)如果target==A[m],那么m就是我们要的结果,直接返回;
(2)如果A[m]<A[r],那么说明从m到r一定是有序的(没有受到rotate的影响),那么我们只需要判断target是不是在m到r之间,如果是则把左边缘移到m+1,否则就target在另一半,即把右边缘移到m-1.
(3)如果A[m]>=A[r],那么说明从l到m一定是有序的,同样只需要判断target是否在这个范围内,相应的移动边缘即可.
根据以上方法,每次我们都可以切掉一半的数据,所以算法的时间复杂度是O(logn),空间复杂度是O(1).
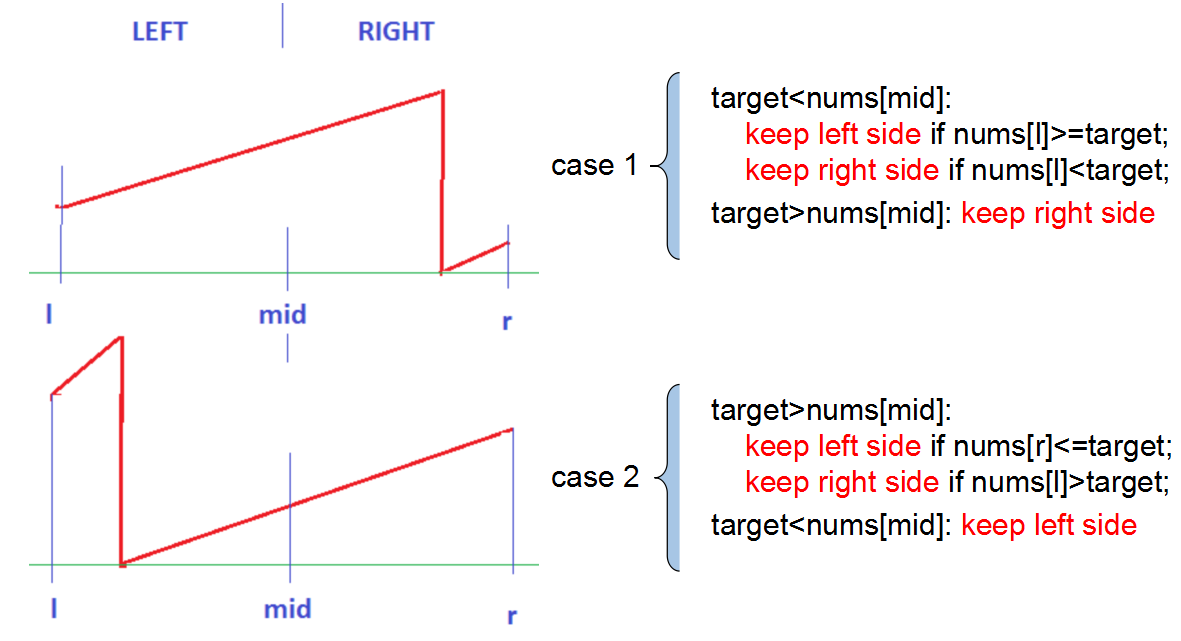
代码如下:
class Solution {
public:
int search(vector<int>& nums, int target) {
int h=0, t=nums.size()-1, m;
while(h<=t){
m = h + (t-h)/2;
if(target==nums[m]) return m;
if(target==nums[h]) return h;
if(target==nums[t]) return t;
if(nums[m] < nums[t])
if(nums[m]<target and target<nums[t]) h=m+1; else t=m-1;
else
if(nums[h]<target and target<nums[m]) t=m-1; else h=m+1;
}
return -1;
}
};我们只能对有序的array采用binary search. 这题告诉我们,半有序的array一样可以用binary search.
这道题用nums[m]和nums[h]比也是可行的. 参见: http://www.tangjikai.com/algorithms/leetcode-binary-search
- Template 2:
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.empty()) return -1;
int h=0, t=nums.size()-1, m;
while(h<t){
m = h + (t-h)/2;
if(target==nums[m]) return m;
if(target==nums[h]) return h;
if(target==nums[t]) return t;
if(nums[m] < nums[t])
if(nums[m]<target and target<nums[t]) h=m+1; else t=m-1;
else
if(nums[h]<target and target<nums[m]) t=m-1; else h=m+1;
}
return nums[h]==target?h:-1;
}
};28.5 81. Search in Rotated Sorted Array II
https://leetcode.com/problems/search-in-rotated-sorted-array-ii/
这道是之前那道 Search in Rotated Sorted Array 在旋转有序数组中搜索 的延伸,现在数组中允许出现重复数字,这个也会影响我们选择哪半边继续搜索,由于之前那道题不存在相同值,我们在比较中间值和最右值时就完全符合之前所说的规律:如果中间的数小于最右边的数,则右半段是有序的,若中间数大于最右边数,则左半段是有序的.而如果可以有重复值,就会出现下面两种情况,[3 1 1] 和 [1 1 3 1],对于这两种情况中间值等于最右值时,目标值3既可以在左边又可以在右边,那怎么办么,对于这种情况其实处理非常简单,只要把最右值向左一位即可继续循环,如果还相同则继续移,直到移到不同值为止,然后其他部分还采用 Search in Rotated Sorted Array 在旋转有序数组中搜索 中的方法.
Update: 其实这道题不用想太多各种情况的讨论,那是不必要的复杂.以如何去重为突破点.比如你要比较的是middle和right,如nums[middle]==nums[right],说明必然有重复,那么去重的方法就是移动指针,当然这里就是移动right,而且只能往后移动.所以就有这样的代码.
class Solution {
public:
int search(vector<int>& nums, int target) {
int h=0, t=nums.size()-1, m;
while(h<=t){
m = h + (t-h)/2;
if(target==nums[m] || target==nums[h] || target==nums[t]) return true;
if(nums[m] < nums[t])
if(nums[m]<target and target<nums[t]) h=m+1; else t=m-1;
else if(nums[m] > nums[t])
if(nums[h]<target and target<nums[m]) t=m-1; else h=m+1;
else //(nums[m] == nums[t])
t--;
}
return false;
}
};28.6 34. Search for a Range
Given a sorted array of integers, find the starting and ending position of a given target value.
Your algorithm's runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
For example,
Given [5, 7, 7, 8, 8, 10] and target value 8,
return [3, 4]
https://leetcode.com/problems/search-for-a-range/
注意本题是找range,所以最后要判定是否nums[h]==target.
vector<int> searchRange(vector<int>& nums, int target) { // O(LogN)
int h=0, t=nums.size()-1, tmp;
while(h<=t){
int m=h+(t-h)/2;
if(target<=nums[m]) t=m-1; else h=m+1;
}
if(h>=nums.size() || nums[h]!=target) return {-1,-1};
tmp=h, h=0, t=nums.size()-1;
while(h<=t){
int m=h+(t-h)/2;
if(target<nums[m]) t=m-1; else h=m+1;
}
return {tmp,t};
}28.7 35. Search Insert Position
https://leetcode.com/problems/search-insert-position/
其实这道题就是Find first euqal to or greater than target.采用上面的套路即可.
28.8 287. Find the Duplicate Number(hard)
https://leetcode.com/problems/find-the-duplicate-number/
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
According to pigeonhole principle: https://en.wikipedia.org/wiki/Pigeonhole_principle
In mathematics, the pigeonhole principle states that if n items are put into m containers, with n > m, then at least one container must contain more than one item.
如果重复一次,那么这道题就简单,可以用二分搜索立刻搞定.
int findDuplicate(vector<int>& nums) {
sort(nums.begin(), nums.end()); // O(NLogN)
int h=0, t=nums.size()-1;
while(h<=t){
int m= h+(t-h)/2;
if(nums[m]!= m+1) t=m-1; else h=m+1;
}
return nums[h];
}但是二分搜索还不是最优,最优的是\(O(N)\)的算法采用swap.
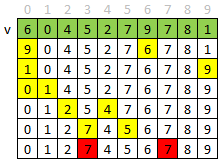
http://www.1point3acres.com/bbs/thread-202691-1-1.html
int find_dup(vector<int> v) {
for (int i = 0; i < v.size(); ++i) {
while (i != v[i]) {
if (v[i] == v[v[i]]) return v[i];
swap(v[i], v[v[i]]);//put v[v[i]] to correct place
}
}
return INT_MAX;
}
void test() {
assert(find_dup({ 6,0,4,5,2,7,9,7,8,1 }) == 7);
}2016(10-12月) 码农类 硕士 全职Bloomberg - 内推 - |Passfresh grad应届毕业生
发个上周五的bloomberg电面攒点rp.两道题,第一道array里所有duplicate intetger.第二道判断tree是否height balanced.dfs做了..
syjohnson 发表于 2016-11-8 12:45 恭喜lc,请问第一题是lc287吗
不是那个.更简单..就找数组里出现次数超过两次的数而已
http://www.1point3acres.com/bbs/thread-209000-1-1.html
题目要求不能改变原数组,而且可以重复多次,那么我们上面的二分法和二分的标准(nums[m]!=m+1)就不能够使用了. 我们需要找另一个合适的二分区间和二分的标准.
假设输入是10个数1,2,4,5,7,7,7,7,8,9. 这里的二分的range是[1,n],假设重复的数字叫D,标准是小于或等于x的数字的个数大于x本身,说明x>=D. 否则x<D. 因此有下面的程序 \(O(NlogN)\):
28.9 153. Find Minimum in Rotated Sorted Array
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
Find the minimum element.
You may assume no duplicate exists in the array.
Example 1:
Input: [3,4,5,1,2]
Output: 1Example 2:
Input: [4,5,6,7,0,1,2]
Output: 0Example 3:
Input: [4,5,6,7]
Output: 4https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/
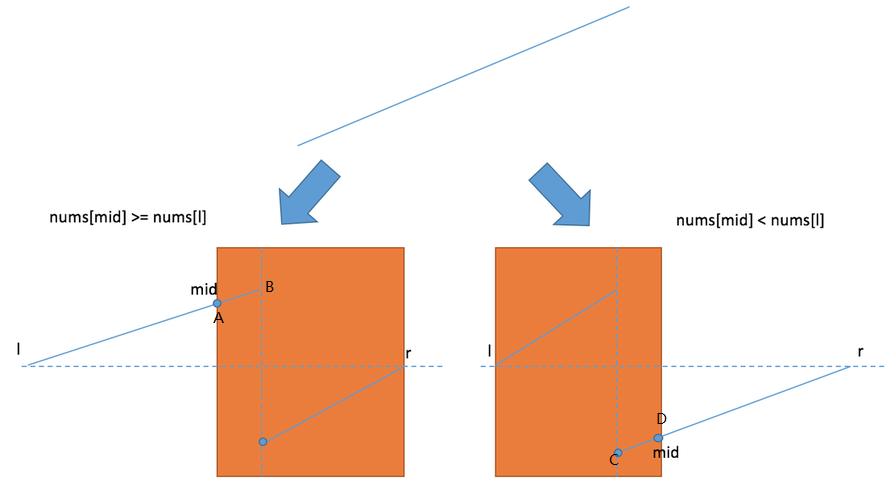
int findMin(vector<int>& nums) {
int h=0, t=nums.size()-1, m;
while(h<=t && nums[h]>nums[t]){
m = h + (t-h)/2;
if(nums[m]>=nums[h]) h=m+1; else t=m;
}
return nums[h];
}这里比较特殊,t=m是因为不能漏掉nums[m]这点.
这个题特殊的两点:1. 每次决定走向的时候是
28.10 154. Find Minimum in Rotated Sorted Array II
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
Find the minimum element.
The array may contain duplicates.
Example 1:
Input: [1,3,5]
Output: 1Example 2:
Input: [2,2,2,0,1]
Output: 0https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/
28.11 162. Find Peak Element
A peak element is an element that is greater than its neighbors.
Given an input array nums, where nums[i] ≠ nums[i+1], find a peak element and return its index.
The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.
You may imagine that nums[-1] = nums[n] = -∞.
Example 1:
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.Example 2:
Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5
Explanation: Your function can return either index number 1 where the peak element is 2,
or index number 5 where the peak element is 6.28.12 852. Peak Index in a Mountain Array
Let’s call an array A a mountain if the following properties hold:
A.length >= 3 There exists some 0 < i < A.length - 1 such that A[0] < A[1] < … A[i-1] < A[i] > A[i+1] > … > A[A.length - 1] Given an array that is definitely a mountain, return any i such that A[0] < A[1] < … A[i-1] < A[i] > A[i+1] > … > A[A.length - 1].
Example 1:
Input: [0,1,0]
Output: 1Example 2:
Input: [0,2,1,0]
Output: 1https://leetcode.com/problems/peak-index-in-a-mountain-array/
28.13 275. H-Index II
Follow up for H-Index: What if the citations array is sorted in ascending order? Could you optimize your algorithm?
https://leetcode.com/problems/h-index-ii
struct Solution {
int hIndex(vector<int>& c) {
int h=0, L=c.size(), t=L-1, m=0;
while(h<=t){
m=h+(t-h)/2;
if(c[m]==L-m)
return L-m;
else if(c[m]<L-m) h=m+1; else t=m-1;
}
return L-h; // return the number, not index
}
};注意H-Index其实是一个个数,最后返回的是个数,所以要用L-h.
28.14 540. Single Element in a Sorted Array
Given a sorted array consisting of only integers where every element appears twice except for one element which appears once. Find this single element that appears only once.
Example 1:
Input: [1,1,2,3,3,4,4,8,8]
Output: 2
Example 2:
Input: [3,3,7,7,10,11,11]
Output: 10
Note: Your solution should run in \(O(log n)\) time and O(1) space.
https://leetcode.com/problems/single-element-in-a-sorted-array/
这道题给我们了一个有序数组,说是所有的元素都出现了两次,除了一个元素,让我们找到这个元素.如果没有时间复杂度的限制,我们可以用多种方法来做,最straightforward的解法就是用个双指针,每次检验两个,就能找出落单的.也可以像Single Number里的方法那样,将所有数字亦或起来,相同的数字都会亦或成0,剩下就是那个落单的数字.那么由于有了时间复杂度的限制,需要为O(logn),而数组又是有序的,不难想到要用二分搜索法来做.二分搜索法的难点在于折半了以后,如何判断将要去哪个分支继续搜索,而这道题确实判断条件不明显,比如下面两个例子:
1 1 2 2 3
1 2 2 3 3这两个例子初始化的时候left=0, right=4一样,mid算出来也一样为2,但是他们要去的方向不同,如何区分出来呢?仔细观察我们可以发现,如果当前数字出现两次的话,我们可以通过数组的长度跟当前位置的关系,计算出右边和当前数字不同的数字的总个数,如果是偶数个,说明落单数左半边,反之则在右半边.有了这个规律就可以写代码了.为啥我们直接就能跟mid+1比呢,不怕越界吗?当然不会,因为left如跟right相等,就不会进入循环,所以mid一定会比right小,一定会有mid+1存在.当然mid是有可能为0的,所以此时当mid和mid+1的数字不等时,我们直接返回mid的数字就可以了.
http://www.cnblogs.com/grandyang/p/7679036.html
O(N):
Binary Search - \(O(Log N)\):
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int h=0, L=nums.size(), t=L-1;
while(h<=t){
cout << h << "," << t << endl;
int m=h+(t-h)/2;
int n=m%2==0?m+1:m-1; // m^1
cout << ">" << m << "," << n << endl;
if(n<L and nums[m]==nums[n]){
h=m+1;
}else{
t=m-1;
}
}
return nums[h];
}
};input: [3,3,7,7,9] output:
0,4
>2,3
3,4
>3,2
4,4
>4,5