Chapter 34 Google 2015

http://www.1point3acres.com/bbs/thread-147786-1-1.html

34.1 Binary Search Tree

如果30分钟内手写不出一个BST的话,你就out了!

34.2 Design Garbage Collector in C++

http://stackoverflow.com/questions/5009869/how-to-implement-garbage-collection-in-c

34.3 149. Max Points on a Line

https://leetcode.com/problems/max-points-on-a-line/

Refer To: linkedin-before-2015

https://segmentfault.com/a/1190000005678407

http://www.cnblogs.com/jcliBlogger/p/4639358.html

复杂度: 时间\(O(N^2)\), 空间\(O(N)\) , N为点数

思路

应知应会:

平面里确定一条直线要两个数据,可以是两个不同的点(高中数学做法),也可以是一个点加一个斜率(这道题做法)

斜率k = (y2 - y1)/(x2 - x1),当 x1 == x2 时,分母为0,斜率为无穷,表示和y轴平行的直线们

在计算机里使用double表示斜率,是不严谨的也是不正确的,double有精度误差,double是有限的,斜率是无限的,无法使用有限的double表示无限的斜率,不过此题的test case没有涉及这个问题

表示斜率最靠谱的方式是用最简分数,即分子分母都无法再约分了.分子分母同时除以他们的最大公约数gcd即可得到最简分数.

gcd对负数也适用. gcd(-100,-10) == -10.

Code:

http://eric-yuan.me/maxpoint/

struct Solution { // 29ms
    int maxPoints(vector<Point> &points) { // 39ms
        int result = 0;
        for(int i=0;i<points.size();i++){
            unordered_map<long long,int> count;
            int same = 1;
            int mx = 0;
            for(int j = i + 1; j < points.size(); j ++){
                int x = points[i].x - points[j].x;
                int y = points[i].y - points[j].y;
                int g = gcd(x, y);
                if(!g){//g==0 means same points
                    same ++;
                    continue;
                }
                x /= g, y /= g;
                mx = max(mx, ++ count[((long long)(x)<<32)|y]);
            }
            result = max(result, mx + same);
        }
        return result;
    }

    int gcd(int num1, int num2) {
        int temp;
        while (num2)
            temp = num2, num2 = num1 % num2, num1 = temp;
        return num1;
    }
};

http://www.cnblogs.com/jcliBlogger/p/4639358.html

struct Solution { // 26ms
    int maxPoints(vector<Point>& points) {
        map<pair<int, int>, int> slopes;
        int maxp = 0, n = points.size();
        for (int i = 0; i < n; i++) {
            slopes.clear();
            int duplicate = 1;
            for (int j = i + 1; j < n; j++) {
                if (points[j].x == points[i].x && points[j].y == points[i].y) {
                    duplicate++;
                    continue;
                }
                int dx = points[j].x - points[i].x;
                int dy = points[j].y - points[i].y;
                int dvs = gcd(dx, dy);
                slopes[make_pair(dx / dvs, dy / dvs)]++;
            }
            maxp = max(maxp, duplicate); 
            for (auto slope : slopes)
                if (slope.second + duplicate > maxp)
                    maxp = slope.second + duplicate;
        } 
        return maxp;
    }
    int gcd(int num1, int num2) {
        while (num2) {
            int temp = num2; 
            num2 = num1 % num2;
            num1 = temp;
        }
        return num1;
    }
};

上面的方法稍微优化以下就是最优解了:

struct Solution { // 16ms Your runtime beats 92.94% of cpp submissions.
int maxPoints(vector<Point>& points) {
    unordered_map<long long, int> slopes;
    int maxp = 0, L = points.size();
    for (int i = 0; i < L; i++) {
        slopes.clear();
        int duplicate = 1;
        for (int j = i + 1; j < L; j++) {
            if (points[j].x == points[i].x && points[j].y == points[i].y) {
                duplicate++;
                continue;
            }
            int dx = points[j].x-points[i].x, dy = points[j].y-points[i].y;
            int dvs = gcd_rec(dx, dy);
            slopes[((long long)(dx/dvs)<<32L)|(dy/dvs)]++;
        }
        maxp = max(maxp, duplicate); //Input: [[0,0]] Expected: 1
        for (auto slope : slopes)
            if (slope.second + duplicate > maxp)
                maxp = slope.second + duplicate;
    } 
    return maxp;
}
/* Recursive:Greatest Common Divisor */
int gcd_rec(int a, int b) { if(b==0)return a;else return gcd_rec(b, a % b);}
int gcd_itr(int num1, int num2) {//iterative
    int temp;
    while (num2)
      temp = num2, num2 = num1 % num2, num1 = temp;
    return num1;
}
};

34.3.1 gcd算法

数学中,辗转相除法,又称欧几里得算法,是求最大公约数的算法.辗转相除法首次出现于欧几里得的《几何原本》(第VII卷,命题yⅠ和Ⅱ)中,而在中国则可以追溯至东汉出现的《九章算术》.

两个整数的最大公约数是能够同时整除它们的最大的正整数.辗转相除法基于如下原理:两个整数的最大公约数等于其中较小的数和两数的相除余数的最大公约数.例如,252和105的最大公约数是21(252 = 21 × 12;105 = 21 × 5);因为252 / 105 = 2余42,所以105和42的最大公约数也是21.在这个过程中,较大的数缩小了,所以继续进行同样的计算可以不断缩小这两个数直至余数变为零.这时的除数就是所求的两个数的最大公约数.由辗转相除法也可以推出,两数的最大公约数可以用两数的整数倍相加来表示,如21 = 5 × 105 + (−2) × 252.这个重要的等式叫做贝祖等式. (http://www.guokr.com/post/569512/)

https://en.wikipedia.org/wiki/Greatest_common_divisor

记忆: 假设gcd(x,y)的参数中第一个x比较小,如果x等于0,返回y;否则返回gcd,两个参数是y%x(大的modulo小的), y(比x小的),放的位置仍然使得第一个数较小,x%y肯定比y小,所以返回的是gcd(y%x,x). 这样就可以写出下面的式子:

[cling]$ int gcd(int x,int y){if(x==0) return y; else return gcd(y%x,x);}
[cling]$ gcd(32,6)
(int) 2
[cling]$ gcd(33,6)
(int) 3

上面的式子比较好记,但其实可以一行搞定: int gcd(int x,int y){return x?gcd(y%x,x):y;}

其实else也是多余的:

// assume a is always greater than b
int gcd(int a, int b) {
  if(b==0) return a;
  // b >= a%b
  return gcd(b, a%b);
}

二刷,注意counter的key是long long.

struct Solution {
  int gcd(int x, int y) { return y ? gcd(y, x%y) : x; }
  int maxPoints(vector<Point>& points) {
    int mx = 0;
    for (int i = 0; i<points.size(); ++i) {
      unordered_map<long long, int> counter;
      int dup = 1;
      int mx_without_dup = 0;
      for (int j = i + 1; j<points.size(); ++j) {
        long long x = points[i].x - points[j].x;////
        int y = points[i].y - points[j].y;
        int d = gcd(x, y);
        if (d == 0) { ++dup; continue; }
        mx_without_dup = max(++counter[((x / d) << 32) | (y / d)], mx_without_dup);
      }
      mx = max(mx_without_dup + dup, mx);
    }
    return mx;
  }
};

34.4 568. Maximum Vacation Days

https://leetcode.com/problems/maximum-vacation-days

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=177167

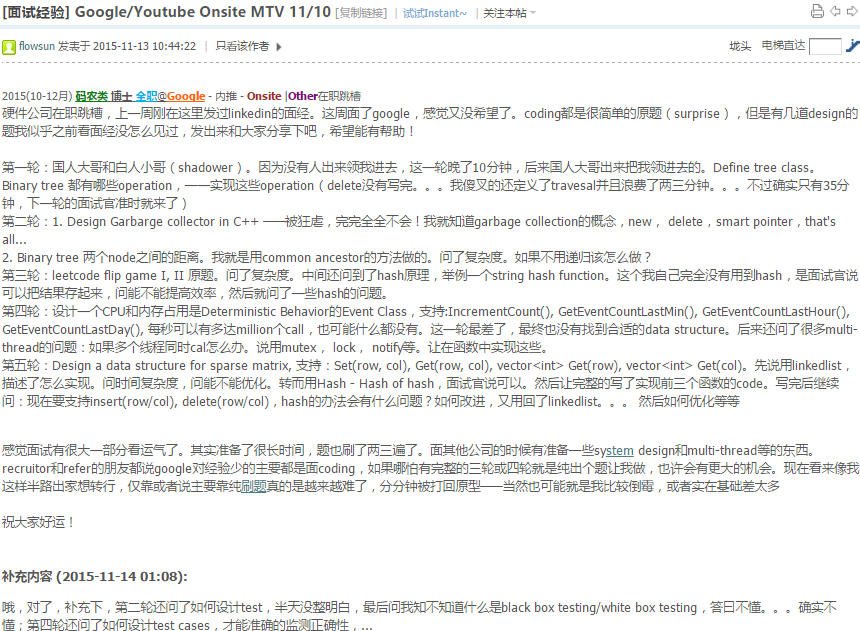
2016(1-3月) 码农类硕士全职 Google - 猎头 - Onsite |Other在职跳槽今天面了 google,也是最近面试非常重要的一次,从昨天晚上就非常紧张,地里的面经看了好多遍. 非常有帮助,今天的面试总结下来,有难有简单,总体来说是meidum 难度偏上,有几道 hard.晚上见证了alphaGo战胜了李世石,感慨科技进步飞快啊卧槽第一轮,linkedlist, 找出最大的两个, 然后swap,不是swap value,swap reference. 第二轮,刚开始主要谈论了一下现在项目,然后写了一个topological sort. 第三轮,RGB颜色转换比如现有#2f3d13, 有16进制的00,33,66,99,cc, ff.要把现有的数字转成最close to这几个数字. 比如#2f3d13 -> #333300; 第二题是findNthsmallest element in BST 第四轮,三道题啊….1. one edit distance 2. wall, flower, matrix找到能看见最多flower的点, 地里高频题 3. count of smaller number before itself. 第五轮,给一个API,O(1)时间计算 sliding window avg, global avg, update(insert) value; 第二题,DP,有几座城市,每个月在每个城市都有不同的假期,然后每个城市有飞往不同城市的航班,求最大能获取的假期和Path. dp(i)(j) 代表第i个月在第j个城市所能获得的最大假期. DP方程大概是 dp(i)(j) = Math.max(dp(i-1)(fromCity)+map(i)(j), dp(i)(j))

总体来说题目有难有简单吧,我觉得多多准备看看面经还是可以的,还有推荐九章的高级算法班(对有一定算法基础的同学),我觉得非常有帮助,至少我觉得有些题,上课老师的讲解和题目对我的帮助很大.

http://www.1point3acres.com/bbs/thread-202732-1-1.html
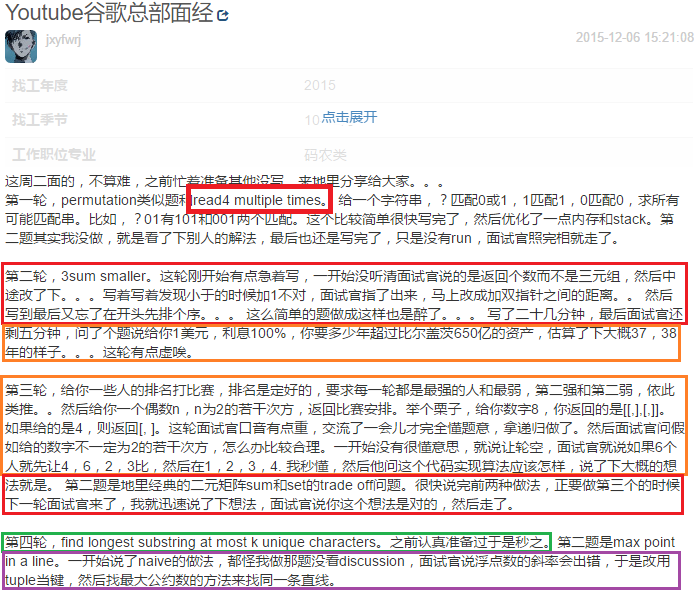
2016(7-9月) 码农类硕士全职 Google - 内推 - Onsite |Other其他
1. 韩国小伙, binary tree的inorder recursive and iterative 两种写法,如何测试.
2. 中国年轻美眉, 实现一个iterator, input 是一个array{3, 8, 0, 12, 2, 9}, 希望输出是 {8, 8, 8, 9, 9}, 也就是eventh number代表词频,oddth number 代表词,{3, 8, 12, 0, 2, 9},就是3个8,0个12,2个9. . 和美眉商量了输入不用array, 用个List 简单好多. 如何测试.

白人小伙. Number of island II,如何测试.
印度老汉. 给一个string, 找出lexical order 最小的,size==k的,subsequence, (note, not substring)

String findMin(String s, k){}

e.g. input: s=pineapple, k==3, output: ale

ale is the lexical order smallest subsequnce of length 3.
我是暴力求解的:

find the first occur position of distinct char.
then start from that position.
dfs to find lenght==3, subsequence(dfs, combination way);
find the one with smallest lexical order.
印度小伙,同时参看上的图
最大假期问题,之前面经看到过这个,但是没有具体的描述,就放过了. 结果就命背的被考到的……….我来详细描述下.
input:

有n个城市,每个城市之间有飞行时间,
给个飞行时间,
给个vacation array, 代表每个城市每周的假期.
从第一个城市开始

意思就是每个周你可以呆在一个城市,然后享受那个城市的假期.还有个限制,就是城市与城市之间的飞行时间不能超过给定的飞行时间.

output:
求x weeks 你能享受到的最大假期总和. 你自己设计输入的数据结构

描述起来真他母亲的繁琐,怪不得没看到详细的说明. .

我的大概想法:

去掉那些飞行时间超过给定飞行时间的边.
用adjancey list做的
然后bfs, 暴力求解.
没写完……

如图所示,最大的应该

week1, A, sum=2; week2, B/C, sum+=1; week3, 回到A, sum+=3 total sum =6

最后两轮都没回答好,可以说写出来80%. 估计是挂了. 发现碰到没做过的题,容易慌,容易去套已经做过的题…,然后思维混乱,就会开始朝令夕改. 还是应该不去套已经做过的题,就从个BF的方法开始. 我都是想搞个优化,结果最后又回到最初的暴力….,郁闷………

34.4.1 Algo 1 - DFS + Pruning

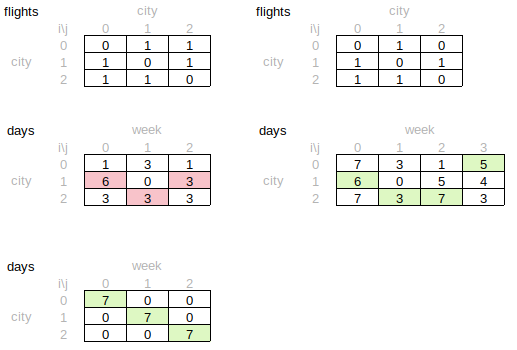
This problem is easier than expected. We can easily come up with a DFS solution.

Brute Force DFS (TS : \(O(n^k)\))

struct Solution {
    int maxVacationDays(vector<vector<int>>& flights, vector<vector<int>>& days) {
        return dfs(flights, days, 0, 0);// week 0 at city 0
    }
    int dfs(vector<vector<int>>& flights, vector<vector<int>>& days, int wk, int cy){
        if(wk == days[0].size()) return 0;
        int r=0;
        for(int i=0; i<flights.size();++i)
            if(cy==i || flights[cy][i]) r=max(r, days[i][wk]+dfs(flights,days,wk+1,i));
        return r;
    }
};

We can cache/memoize the repeatedly-calculated intermediate results:

struct Solution { // beat 30%
    vector<vector<int>> cache;// a matrix where row is city and column is week
    int maxVacationDays(vector<vector<int>>& flights, vector<vector<int>>& days) {
        cache=vector<vector<int>>(flights.size(), vector<int>(days[0].size(),-1));
        return dfs(flights, days, 0, 0);
    }
    int dfs(vector<vector<int>>& flights, vector<vector<int>>& days, int wk, int cy){
        if(wk == days[0].size()) return 0;
        if(cache[cy][wk]>0) return cache[cy][wk];
        int r=0;
        for(int i=0; i<flights.size();++i)
            if(cy==i || flights[cy][i]) r=max(r, days[i][wk]+dfs(flights,days,wk+1,i));
        return cache[cy][wk]=r;// cache result
    }
};

34.4.2 Algo 2 - DP

经过上面的思考,这道题和Paint House非常相似. Actually we can use DFS+Pruning to solve Paint House too.

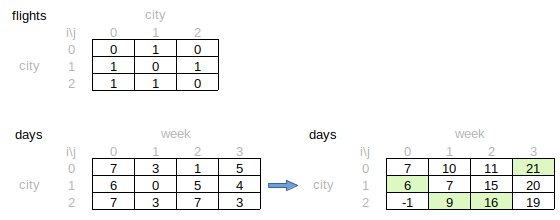
Time complexity : \(O(n^2 k)\), SC: \(O(1)\) No extra space.

struct Solution {
    int maxVacationDays(vector<vector<int>>& flights, vector<vector<int>>& days) {
        int R=days.size(), C=days[0].size();
        for(int i=0;i<R;++i)
            if(i!=0 && flights[0][i]==0) days[i][0]=-1;
        for(int wk=1;wk<C;++wk){
            for(int cy=0;cy<R;++cy){
                int t=-1;
                for(int j=0;j<R;++j)
                    if(j==cy || flights[j][cy]) t=max(t, days[j][wk-1]);
                if(t==-1) days[cy][wk]=-1; else days[cy][wk] += t;
            }
        }
        int r=0;
        for(int i=0;i<R;++i) r=max(r,days[i][C-1]);
        return r;
    }
};

这道题比Paint House复杂的地方是,因为始终从city 0出发,有可能有些不能到达的城市,对不能到达的城市,不能采用累加的办法.这里我们用-1标记不能到达的cell.否则下面的case通不过.

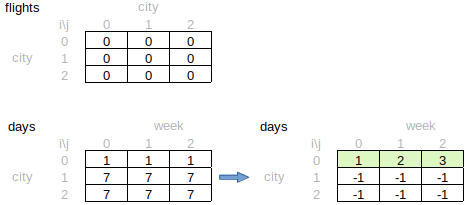
此外leetcode官方的文章是采用的从后往前推的方式,结果一样: https://leetcode.com/articles/maximum-vacation-days/