Chapter 19 Binary Search Tree

Binary tree is a very beautiful data structure, so the code is supposed to be beautiful as well. If not, think twice!

Binary Tree is a simplified version of Graph, or a complex version of linked list!!

Three tools to solve 90% binary tree problems:

Recursion
DFS
BFS

It tests the understanding of DFS, BFS, Recursion.

https://www.hrwhisper.me/leetcode-tree/

https://leetcode.com/problems/serialize-and-deserialize-binary-tree/

Transform/Manipulation of Binary Tree

19.1 108. Convert Sorted Array to Binary Search Tree

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:
Given the sorted array: [-10,-3,0,5,9],
One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/

class Solution {
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return rec(nums,0,nums.size()-1);
    }
    TreeNode* rec(vector<int>& nums, int h, int t){
        if(h>t) return 0;
        int m = h+(t-h)/2;
        TreeNode* R= new TreeNode(nums[m]);
        R->left  = rec(nums,h,m-1);
        R->right = rec(nums,m+1,t);
        return R;
    }
};

19.2 109. Convert Sorted List to Binary Search Tree

https://leetcode.com/problems/convert-sorted-list-to-binary-search-tree/

Given a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST

我们知道,对于一个二叉树来说,左子树一定小于根节点,而右子树大于根节点.所以我们需要找到链表的中间节点,这个就是根节点,链表的左半部分就是左子树,而右半部分则是右子树,我们继续递归处理相应的左右部分,就能够构造出对应的二叉树了.

这题的难点在于如何找到链表的中间节点,我们可以通过fast,slow指针来解决,fast每次走两步,slow每次走一步,fast走到结尾,那么slow就是中间节点了.

struct Solution {
  TreeNode *sortedListToBST(ListNode *head) {
      return build(head, NULL);
  }
  TreeNode* build(ListNode* h, ListNode* e) {
      if(h == e) return NULL;
      ListNode *fast = h, *slow = fast;
      while(fast != e && fast->next != e) // upper median
          slow = slow->next, fast = fast->next->next;
      TreeNode* node = new TreeNode(slow->val);
      node->left = build(h, slow);
      node->right = build(slow->next, e);
      return node;
  }
};

Another AC code to use lower median as root:

struct Solution_LowerMeidan {
  TreeNode *sortedListToBST(ListNode *head) {
      return build(head, NULL);
  }
  TreeNode* build(ListNode* h, ListNode* e) {
      if(h == e) return NULL;
      ListNode *fast = h, *slow = fast;
      while(fast->next != e && fast->next->next != e) // lower median
          slow = slow->next, fast = fast->next->next;
      TreeNode* node = new TreeNode(slow->val);
      node->left = build(h, slow);
      node->right = build(slow->next, e);
      return node;
  }
};

Linked List Lower Median:

      while(fast->next != e && fast->next->next != e) // lower median
          slow = slow->next, fast = fast->next->next;

Linked List Upper Median:

      while(fast != e && fast->next != e) // upper median
          slow = slow->next, fast = fast->next->next;

比较:
linked-list.html#palindrome-linked-list
linked-list.html#linked-list-cycle

19.3 AVL tree

An AVL tree is a BST where the height of every node and that of its sibling differ by at most 1.

https://github.com/mission-peace/interview/blob/master/src/com/interview/tree/AVLTree.java

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=208621

19.4 `Order Statistic Tree` and `Stream Median Tree`

19.5 Find Median from Data Stream

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples: [2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

void addNum(int num) - Add a integer number from the data stream to the data structure. double findMedian() - Return the median of all elements so far.

For example:

add(1)
add(2)
findMedian() -> 1.5
add(3)
findMedian() -> 2

19.5.1 Method 1: Two heaps

T: O(LogN)

19.5.2 Method 2: Order Statistic Tree

T: O(LogN)

CLRS p473 Amortized weight-balanced trees

https://en.wikipedia.org/wiki/Order_statistic_tree

http://www.cs.cornell.edu/courses/cs211/2004su/slides/Topic20b.pdf

http://stackoverflow.com/questions/11230734/c-stl-order-statistic-tree

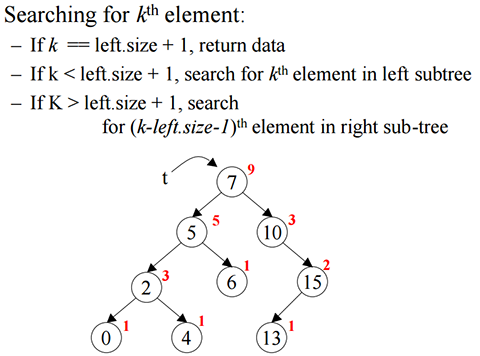
https://gcc.gnu.org/onlinedocs/libstdc++/manual/policy_data_structures_design.html#container.tree.interface

http://opensource.apple.com//source/llvmgcc42/llvmgcc42-2336.9/libstdc++-v3/testsuite/ext/pb_ds/example/tree_order_statistics.cc

public class MedianFinder {
  public static class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    int t;
    TreeNode(int x) { this.val = x; this.t = 1; }
  }
  TreeNode root = null;
  int count = 0;

  public void add(int num) {
    count++;
    root = insertNode(root, num);
  }
  public TreeNode insertNode(TreeNode root, int num) {
    if (root == null) {
      return new TreeNode(num);
    }
    if (root.val > num) {
      root.left = insertNode(root.left, num);
    } else {
      root.right = insertNode(root.right, num);
    }
    root.t++;
    return root;
  }
  public int find(int k) {
    TreeNode cur = root;
    int rst = 0;
    while (cur != null) {
      int l = 0;
      if (cur.left == null) {
        l = 0;
      } else {
        l = cur.left.t;
      }
      if (cur.left != null && l >= k) {
        cur = cur.left;
      } else if (cur.right != null && l < k - 1) {
        cur = cur.right;
        k = k - 1 - l;
      } else {
        rst = cur.val;
        break;
      }
    }
    return rst;
  }
  public int size() {
    return count;
  }
  // Adds a number into the data structure.
  public void addNum(int num) {
    this.add(num);
  }
  // Returns the median of current data stream
  public double findMedian() {
    int s = this.size();
    double rst = 0;
    if (s % 2 == 1) {
      rst = this.find(s / 2 + 1);
    } else {
      int f1 = this.find(s / 2);
      int f2 = this.find(s / 2 + 1);
        rst = (f1 + f2) / 2.0;
    }
    return rst;
  }
};

19.5.3 Method 3: Median Binary Tree

T: O(1)

This solution uses an ordinary binary tree for simplicity’s sake, which means it is likely to be unbalanced. Given enough time one may well use a balanced binary tree implementation to guarantee O(logn) runtime for addNum(). It is easy to see that findMedian() runs in O(1).

By using a binary tree, we can easily keep the input numbers in nondecreasing order. Observe that whenever a number is added, the numbers used to calculate the median never shift by more than 1 position (in an imagined array representation) to the left or to the right. Let’s see an example: [2], number used to calculate median is 2. [2,3], numbers used are 2,3 (expanding 1 to right) [0,2,3], use 2 (shrinking 1 to left) [0,1,2,3], use 1,2 (expanding 1 to left) [0,1,2,3,4], use 2 (shrinking 1 to right) ….and so on.

With this observation, in MedianFinder I employ 2 variables medianLeft and medianRight to keep track of numbers we need to calculate the median. When size is odd, they point to the same node, otherwise they always point to 2 nodes which have predecessor/successor relationship. When adding a node, we just need to check the size of our MedianFinder tree, then depending on whether the new number is inserted to the left, inbetween, or to the right of our 2 median trackers, we will change medianLeft and medianRight to point to the correct nodes. Because the position never shifts more than 1, we can simply use predecessor() or successor() on the desired node to update it. Those 2 methods run in O(logn) when the tree is balanced, hence the O(logn) runtime of addNum().

public class MedianFinder {
    private Node root;
    private Node medianLeft;
    private Node medianRight;
    private int size;
    public MedianFinder() { }
    // Adds a number into the data structure.
    public void addNum(int num) {
        if (root == null) {
            root = new Node(num);
            medianLeft = root;
            medianRight = root;
        } else {
            root.addNode(num);
            ////!!!! adjust medianLeft and medianRight
            if (size % 2 == 0) {
                if (num < medianLeft.data) {
                    medianRight = medianLeft;
                } else if (medianLeft.data <= num && num < medianRight.data) {
                    medianLeft = medianLeft.successor();
                    medianRight = medianRight.predecessor();
                } else if (medianRight.data <= num) {
                    medianLeft = medianRight;
                }
            }
            else {
                if (num < medianLeft.data) {
                    medianLeft = medianLeft.predecessor();
                }
                else {
                    medianRight = medianRight.successor();
                }
            }
        }
        size++;
    }
    // Returns the median of current data stream
    public double findMedian() {
        return (medianLeft.data + medianRight.data) / 2.0;
    }
    class Node {
        private Node parent; //
        private Node left;
        private Node right;
        private int data;
        public Node(int data) { this.data = data; }
        public void addNode(int data) {
            if (data >= this.data) {
              if (right == null) {
                right = new Node(data);
                right.parent = this;
              }
              else
                right.addNode(data);
            }
            else {
              if (left == null) {
                left = new Node(data);
                left.parent = this;
              }
              else
                left.addNode(data);
            }
        }
        public Node predecessor() {               
            if (left != null)
                return left.rightMost();
            Node predecessor = parent;
            Node child = this;
            while (predecessor != null && child != predecessor.right) {
                child = predecessor;
                predecessor = predecessor.parent;
            }
            return predecessor;
        }
        public Node successor() {
            if (right != null)
                return right.leftMost();
            Node successor = parent;
            Node child = this;
            while (successor != null && child != successor.left) {
                child = successor;
                successor = successor.parent;
            }
            return successor;
        }
        public Node leftMost(){
            if (left == null)
                return this;
            return left.leftMost();
        }
        private Node rightMost() {
            if (right == null)
                return this;
            return right.rightMost();
        }
    }
};

19.6 Identical BST

https://www.careercup.com/question?id=19016700

19.7 98. Validate Binary Search Tree

Given a binary tree, determine if it is a valid binary search tree (BST).

Assume a BST is defined as follows:

The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.

Example 1:

    2
   / \
  1   3

Binary tree [2,1,3], return true.

Example 2:

    1
   / \
  2   3

Binary tree [1,2,3], return false.

https://leetcode.com/problems/validate-binary-search-tree

用inorder traversal的结果是sorted array的性质可以解题. 下面是递归解法. 这个解法感觉很优美.

A Tree is BST if following is true for every node x:
- The largest value in left subtree (of x) is smaller than value of x.
- The smallest value in right subtree (of x) is greater than value of x.

struct Solution {
    bool isValidBST(TreeNode *root) {
        return dfs(root, LONG_MIN, LONG_MAX);
    }
    bool dfs(TreeNode *root, long mi, long mx) {
        if (!root) return true;
        if (root->val <= mi || root->val >= mx) return false;
        return dfs(root->left, mi, root->val) && dfs(root->right, root->val, mx);
    }
};

http://www.cnblogs.com/grandyang/p/4298435.html 详细的讲解,里面提到的等于的情况和CLRS的定义不同.

19.8 333. Largest BST Subtree

Given a binary tree, find the largest subtree which is a Binary Search Tree (BST), where largest means subtree with largest number of nodes in it.

Note: A subtree must include all of its descendants.

Here’s an example:

The Largest BST Subtree in this case is the highlighted one. The return value is the subtree’s size, which is 3.

Follow up: Can you figure out ways to solve it with O(n) time complexity?

https://leetcode.com/problems/largest-bst-subtree

http://www.geeksforgeeks.org/find-the-largest-subtree-in-a-tree-that-is-also-a-bst/
http://www.geeksforgeeks.org/largest-bst-binary-tree-set-2/
http://www.cnblogs.com/grandyang/p/5188938.html

19.8.1 Algo 1: Recursion

这个解法很自然,写法很简洁.但是T: \(O(N^2)\)

struct Solution {
    int largestBSTSubtree(TreeNode* root) {
        if (!root) return 0;
        if (isValid(root, INT_MIN, INT_MAX)) return count(root);
        return max(largestBSTSubtree(root->left), largestBSTSubtree(root->right));
    }
    bool isValid(TreeNode* root, int mi, int mx) {
        if (!root) return true;
        if (root->val <= mi || root->val >= mx) return false;
        return isValid(root->left, mi, root->val) && isValid(root->right, root->val, mx);
    }
    int count(TreeNode* root) {
        if (!root) return 0;
        return count(root->left) + count(root->right) + 1;
    }
};

19.8.2 Algo 2:

先递归到最左子节点,然后逐层往上递归,对于每一个节点,我们都记录当前最大的BST的节点数,当做为左子树的最大值,和做为右子树的最小值,当每次遇到左子节点不存在或者当前节点值大于左子树的最大值,且右子树不存在或者当前节点值小于右子树的最小数时,说明BST的节点数又增加了一个,我们更新结果及其参数,如果当前节点不是BST的节点,那么我们更新BST的节点数res为左右子节点的各自的BST的节点数的较大值,参见代码如下:

struct Solution {
    int largestBSTSubtree(TreeNode* root) {
        int res = 0, mi = INT_MIN, mx = INT_MAX;
        bool d = isValidBST(root, mi, mx, res);
        return res;
    }
    bool isValidBST(TreeNode *root, int &mi, int &mx, int &res) {
        if (!root) return true;
        int left_n = 0, right_n = 0, left_mi = INT_MIN;
        int right_mi = INT_MIN, left_mx = INT_MAX, right_mx = INT_MAX;
        bool left  = isValidBST(root->left,  left_mi,  left_mx,  left_n);
        bool right = isValidBST(root->right, right_mi, right_mx, right_n);
        if (left && right) {
            if ((!root->left || root->val > left_mx) && (!root->right || root->val < right_mi)) {
                res = left_n + right_n + 1;
                mi = root->left ? left_mi : root->val;
                mx = root->right ? right_mx : root->val;
                return true;
            }
        }
        res = max(left_n, right_n);
        return false;
    }
};

19.9 250. Count Univalue Subtrees

Given a binary tree, count the number of uni-value subtrees.

A Uni-value subtree means all nodes of the subtree have the same value.

For example: Given binary tree,

return 4.

https://leetcode.com/problems/count-univalue-subtrees

subtree就是指,在一个tree里的某一个node,以及这个node的所有descendants.那么从题目给的例子里,我们复合条件的subtree有4个, 左边第三层里的两个“5”算其2, 右边第二层的“5 - 5”,以及第三层的“5”也都算符合条件的subtree,所以我们返回4.

struct Solution {
    int count = 0;
    int countUnivalSubtrees(TreeNode* root) {
        if(!root) return 0;
        univalue(root);
        return count;
    }
    bool univalue(TreeNode* n){
        if(!n) return true; //if(!n->left && !n->right) return ++count; // not necessary
        bool l=univalue(n->left);
        bool r=univalue(n->right);
        if(!l || !r) return false;
        if((n->left && n->left->val!=n->val)||(n->right && n->right->val!=n->val)) return false;
        return ++count;
    }
};

19.10 99. Recover Binary Search Tree

Two elements of a binary search tree (BST) are swapped by mistake.
Recover the tree without changing its structure.

Note: A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

https://leetcode.com/problems/recover-binary-search-tree/

class Solution {
    TreeNode *_1st=0, *_2nd=0, *prev=0;
public:
    void recoverTree(TreeNode* R) {
        TreeNode t(INT_MIN);
        prev = &t;
        dfs(R);
        swap(_1st->val, _2nd->val);
    }
    void dfs(TreeNode* n){
        if(!n) return;
        dfs(n->left);
        if (!_1st && prev->val >= n->val) _1st = prev;
        if (_1st && prev->val >= n->val)  _2nd = n; // no `else if` here
        prev = n;
        dfs(n->right);
    }
};

http://bit.ly/2enqrxl, http://bit.ly/2envTjv

Morris Traversal: http://bit.ly/2iKad6c

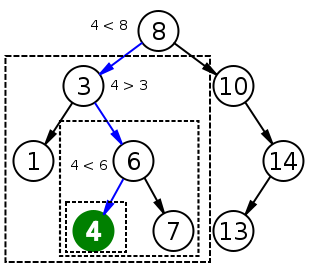
19.11 669. Trim a Binary Search Tree

Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.

https://leetcode.com/problems/trim-a-binary-search-tree

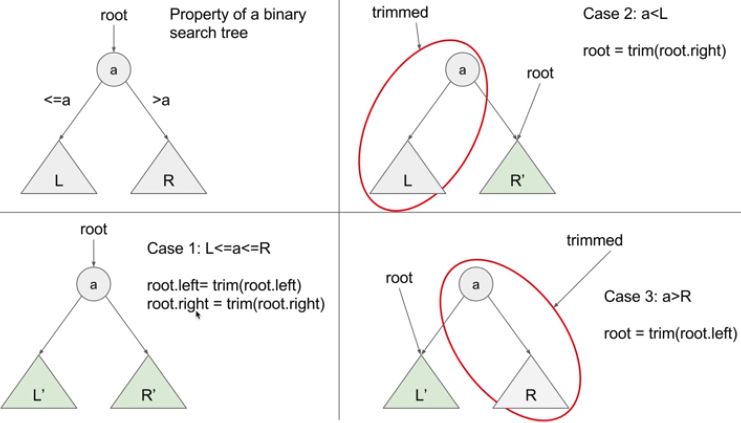
struct Solution {
    TreeNode* trimBST(TreeNode* R, int l, int r) {
        if(!R) return 0;
        if(R->val<l) return trimBST(R->right,l,r);
        if(R->val>r) return trimBST(R->left,l,r);
        R->left=trimBST(R->left, l, r);
        R->right=trimBST(R->right, l, r);
        return R;
    }
};

We must visit every node once…so O(N); where N is the number of nodes in our tree.

To delete the nodes:
https://leetcode.com/problems/trim-a-binary-search-tree/discuss/107046/C++-recursion

19.12 776. Split BST

Given a Binary Search Tree (BST) with root node root, and a target value V, split the tree into two subtrees where one subtree has nodes that are all smaller or equal to the target value, while the other subtree has all nodes that are greater than the target value. It’s not necessarily the case that the tree contains a node with value V.

Additionally, most of the structure of the original tree should remain. Formally, for any child C with parent P in the original tree, if they are both in the same subtree after the split, then node C should still have the parent P.

You should output the root TreeNode of both subtrees after splitting, in any order.