Chapter 56 Linkedin 2017 Interview Questions Part 3

56.1 a==b but ++a != ++b

Me:
除了overflow, overload,multithread还有没有?
rainnight🐢龟兔赛跑:
你说完我想到的了
Me:
再想想
徐晨 q4 纽约:
reference?
Me:
我又想到一个macro
Eric SGI 费城:
a b type 不同也可以啊
Me:
reference作何解?
Me:
@Eric 当然
徐晨 q4 纽约:
A和B都是指向一个object的ref
Me:
牛

56.2 Sparse Matrix Storage

http://www.alglib.net/matrixops/sparse.php

2017(1-3月) 码农类博士全职@Linkedin - 内推 - Onsite |Failfresh grad应届毕业生年初的onsite第一轮:两个国人小哥,两个题,第一个题目是判断一个数组中有没有三个数能组成一个三角形,第一轮面试,完全没状态,很简单的题我却花了很久,这轮应该挂了;第二个题目是给一个数字组成的sequence和一个target, 可以在数字之间加 + - * / 四种运算法,返回可以算出计算结果是target的string, 递归做第二轮:问如何设计一个model判断一条信息是不是广告第三轮:第一题是类似于find the kth largest number的变体;第二个题题目小哥打印出来了,题目就一张纸,是关于矩阵存储的,但是细细分析下,题目并不难,代码不多. 第四轮:hr面,问自己的project和各种behavioal question, 为什么linkedIn啊,以后的打算啊之类的题目超长、有一页纸,大概是说一个size特别大的sparse matrix, 如何用少数的几个参数来存储这个大matrix, 具体的我忘记了,太久了,但是不难

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=270287

https://www.karlrupp.net/2016/02/sparse-matrix-transposition-datastructure-performance-comparison/
http://blog.csdn.net/fanzheng220112583/article/details/7715003
http://10788311.blog.51cto.com/10778311/1764868
https://www.smcm.iqfr.csic.es/docs/intel/mkl/mkl_manual/appendices/mkl_appA_SMSF.htm

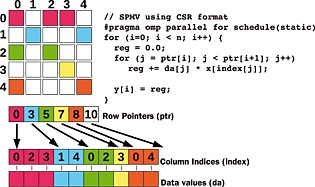
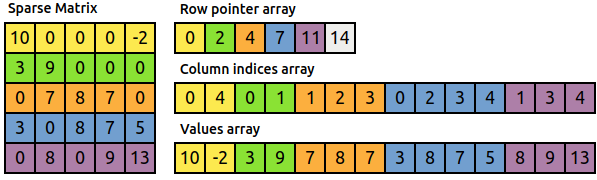
56.2.1 Compressed Sparse Row Format (CSR)

https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.sparse.csr_matrix.html

注意row pointer index的定义: (https://en.wikipedia.org/wiki/Sparse_matrix#Compressed_sparse_row_.28CSR.2C_CRS_or_Yale_format.29)第一个值一定是0,然后每行有个数表示这行的非0元素的数目.所以根据定义,row number等于row pointer vector的长度-1. 还有其实row pointer index其实是一个cumulative vector.

但是,CSR格式的column number是未知的其实.

>>> from scipy.sparse import *
>>> from scipy import *
>>> row = array([0,0,1,2,2,2])
>>> col = array([0,2,2,0,1,2])
>>> data = array([1,2,3,4,5,6])
>>> x=csr_matrix( (data,(row,col)), shape=(3,8) )
>>> x.todense()
matrix([[1, 0, 2, 0, 0, 0, 0, 0],
        [0, 0, 3, 0, 0, 0, 0, 0],
        [4, 5, 6, 0, 0, 0, 0, 0]])

In the following program, we will find a matrix with the minimum column size.

vector<vector<int>> csr2dense(vector<int>& rptr,
  vector<int>& cidx, vector<int>& val)
{
  int ROW = rptr.size() - 1,
    COL = *max_element(cidx.begin(), cidx.end()) + 1;
  vector<vector<int>> r(ROW, vector<int>(COL));
  int ri = 0;
  for (int i = 0; i <ROW; ++i)
    for (int j = rptr[i]; j < rptr[i + 1]; ++j)
      r[i][cidx[j]] = val[j];
  return r;
}

定义csr为一个类,并求两个sparse matrix的点积:

class csr {
  vector<int> rptr;
  vector<int> cidx;
  vector<int> data;
};
csr dotproduct(csr& l, csr& r){
  return r;
}

http://www.scipy-lectures.org/advanced/scipy_sparse/csr_matrix.html#examples

https://op2.github.io/PyOP2/linear_algebra.html

http://stackoverflow.com/questions/12129948/scipy-sparse-set-row-to-zeros

56.2.1.1 Dot Product

http://eigen.tuxfamily.org
http://eigen.tuxfamily.org/dox/group__TutorialSparse.html

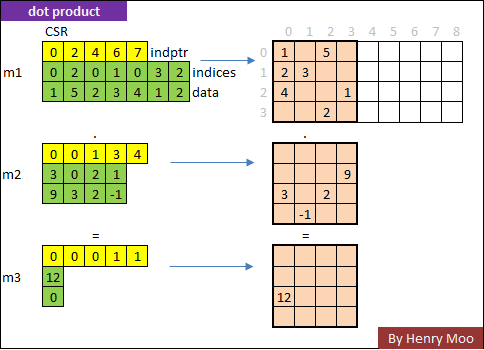
In Scipy:

>>> from scipy.sparse import *
>>> from scipy import *
>>> data
[1, 5, 2, 3, 4, 1, 2]
>>> indptr
[0, 2, 4, 6, 7]
>>> indices=[0, 2, 0, 1, 0, 3, 2]
>>> m1= csr_matrix( (data,indices,indptr), shape=(4,4) )
>>> m1.data
array([1, 5, 2, 3, 4, 1, 2])
>>> m2= csr_matrix( ([0,3,2,-1],[3,0,2,1],[0,0,1,3,4]), shape=(4,4) )
>>> m3=m1.multiply(m2)
>>> m3.data
array([12])
>>> m3.indices
array([0], dtype=int32)
>>> m3.indptr
array([0, 0, 0, 1, 1], dtype=int32)

56.2.1.2 Set Row/Column to Zeros

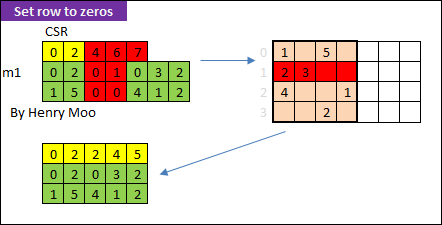
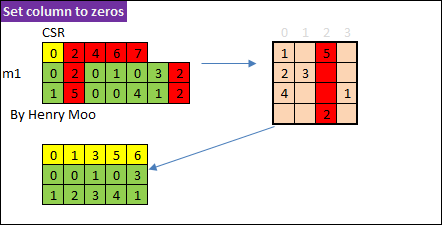
In Scipy:
http://stackoverflow.com/questions/12129948/scipy-sparse-set-row-to-zeros

from scipy.sparse import *
from scipy import *
def csr_row_set_nz_to_val(csr, row, value=0):
    """Set all nonzero elements (elements currently in the sparsity pattern)
    to the given value. Useful to set to 0 mostly.
    """
    if not isinstance(csr, scipy.sparse.csr_matrix):
        raise ValueError('Matrix given must be of CSR format.')
    csr.data[csr.indptr[row]:csr.indptr[row+1]] = value

data=[1, 5, 2, 3, 4, 1, 2]
indices=[0, 2, 0, 1, 0, 3, 2]
indptr=[0, 2, 4, 6, 7]
m1= csr_matrix( (data,indices,indptr), shape=(4,4) )
for row in indices: csr_row_set_nz_to_val(m1, row, 0)
m1.eliminate_zeros()
m1.todense()
"""matrix([[0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0],
        [0, 0, 0, 0]])"""

In Eigen:

https://eigen.tuxfamily.org/dox/classEigen_1_1SparseMatrix.html

Code at: /opt/share/eigen/Eigen/src/SparseCore

$apt-get install libeigen3-dev -y
$g++ sparsematrix.cpp -o sparsematrix -I /usr/include/eigen3/
$./sparsematrix
Nonzero entries:
(-0.211234,0) (0.257742,1) (0.678224,3) (0.539828,4)
(-0.604897,0) (0.83239,1) (0.0485743,3) (-0.295083,4)
(0.536459,0) (0.434594,1) (0.94555,3) (0.838053,4)
(0.10794,0) (0.213938,1) (0.542715,3) (0.898654,4)

Outer pointers:
0 4 4 8 12  $

-0.211234 0.257742 0 0.678224 0.539828
0 0 0 0 0
-0.604897 0.83239 0 0.0485743 -0.295083
0.536459 0.434594 0 0.94555 0.838053
0.10794 0.213938 0 0.542715 0.898654
$ccat sparsematrix.cpp
#include <Eigen/Sparse>
#include <iostream>
using namespace Eigen;
int main() {
  Eigen::SparseMatrix<float, Eigen::RowMajor> A;
  A = MatrixXf::Random(5,5).sparseView();
  A.prune([](int i, int j, float) { return i!=1 && j!=2; });
  std::cout << A << "\n";
}

56.2.2 Compressed Sparse Column Format (CSC)

http://www.scipy-lectures.org/advanced/scipy_sparse/csc_matrix.html

Counter for frequency calculation?

http://www.1point3acres.com/bbs/thread-90856-1-1.html

56.2.3 Orthogonal List

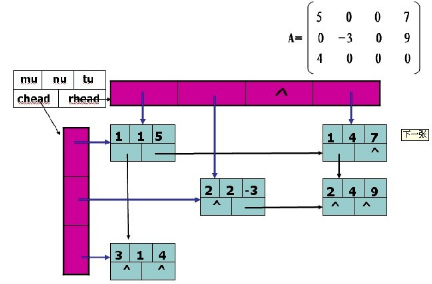
http://blog.csdn.net/zhuyi2654715/article/details/6729783
http://blog.sina.com.cn/s/blog_7671b3eb0100q4p5.html

用三元组表法表示的稀疏矩阵,比起用二维数组存储,节约了空间,并且使得矩阵某些运算的运算时间比经典算法还少.但是,在进行矩阵加法、减法和乘法等运算时,有时矩阵中的非零元素的位置和个数会发生很大的变化.如A=A+B,将矩阵B加到矩阵A上,此时,若还用三元组的表示法,势必会为了保持三元组表“以行序为主序”,而大量移动元素.为了避免大量移动元素,这一节我们介绍稀疏矩阵的链式存储法—–十字链表,它能够灵活地插入因运算而产生的新的非零元素、删除因运算而产生的新的零元素,实现矩阵的各种运算.

供了解,实现太麻烦了

http://ultra.pr.erau.edu/~jaffem/classes/cs315/cs315_homework/homework/sparse.htm