Chapter 13 Heap
https://algs4.cs.princeton.edu/61event/
13.1 Basics
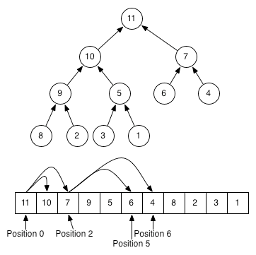
注意priority_queue的定义是如果有first,last,就放在最前,之后是comparator,再之后是container.
template< class InputIt >
priority_queue( InputIt first, InputIt last, const Compare& compare, const Container& cont );- Index calculation
in a 0-based index array:
From parent to children, left child: 2i+1, right child: 2i+2
From Child to parent: (i-1)/2
13.2 difference between segment-tree
segment tree - all leaves are from input; inner nodes are from computing
l child: 2i, r child: 2i+1
heap - all nodes are from input
13.3 Index Heap
Algorithms 4ed Sedgewick Page 332
- Stock/IP Statistics(index priority queue)
bimap + max-heap + insertion sort or min-heap (topK)
struct index_priority_queue {
vector<int> volumes; // 100 items
unordered_map<int, string> index2ticker;
unordered_map<string, int> ticker2index;
int size = 0;
index_priority_queue(int hsize = 100) { volumes.resize(hsize); }
// ix - index1, iy - index2
void __swap(int ix, int iy) {
std::swap(volumes[ix], volumes[iy]);
std::swap(ticker2index[index2ticker[ix]], ticker2index[index2ticker[iy]]);
std::swap(index2ticker[ix], index2ticker[iy]);
}
void push(string s, int v) { // O(LogN)
volumes[size] = v;
index2ticker[size] = s;
ticker2index[s] = size;
int cindex = size;
int pindex = PAR(size);
while (pindex >= 0 && volumes[pindex]<volumes[cindex]) {
__swap(cindex, pindex);// swap with its parent
cindex = pindex;
pindex = PAR(pindex);
}
++size;
}
// update can be decrease or increase ??
void update(string ticker, int new_volume) { // O(LogN)
if (ticker2index.find(ticker) == ticker2index.end()) {
push(ticker, new_volume);
return;
}
int cur_idx = ticker2index[ticker]; // current index
volumes[cur_idx] = new_volume;
// 1. increment - swap with its parent (sift up)
int pindex = PAR(cur_idx);
while (pindex >= 0 && volumes[pindex] < volumes[cur_idx]) { // LogN
__swap(cur_idx, pindex);
cur_idx = pindex;
pindex = PAR(pindex);
}
// 2. decrement - swap with the bigger of its children (sift down)
int greater_lc_rc = -1;
while (1) { // LogN
int lc = LEF(cur_idx), rc = RIG(cur_idx);
if (rc<size) {
greater_lc_rc = (volumes[lc] > volumes[rc]) ? lc : rc;
} else if (rc == size) {
greater_lc_rc = lc;
} else break;
if (greater_lc_rc>0 && volumes[cur_idx]<volumes[greater_lc_rc]) {
__swap(cur_idx, greater_lc_rc);
cur_idx = greater_lc_rc;
} else break;
}
}
// Get topK from heap with help of a new size-k heap in O(KLogK)
void topK(int k) { // O(KLogK) where K==10
vector<pair<string, int>> vp;
priority_queue<pair<int,int>> pq; // pair of {volume, index}
pq.push({volumes[0],0});
while (k-- && !pq.empty()) {
auto pr = pq.top(); pq.pop();
vp.emplace_back(index2ticker[pr.second],volumes[pr.second]);
int lc = LEF(pr.second), rc = RIG(pr.second);
if (lc<size) pq.push(pair<int, int>({ volumes[lc], lc })); // LogK
if (rc<size) pq.push(pair<int, int>({ volumes[rc], rc }));
}
}
};关键思想: 取走顶点,并把顶点的左右儿子都加入新heap
13.4 D-ary Heap
http://blog.mischel.com/2013/10/05/the-d-ary-heap/
Java Implementation:
http://en.algoritmy.net/article/41909/D-ary-heap
http://www.sanfoundry.com/java-program-implement-d-ary-heap/
Applications of D-ary Heap:
D-ary heap when used in the implementation of priority queue allows faster decrease key operation as compared to binary heap ( O(log2n)) for binary heap vs O(logkn) for D-ary heap). Nevertheless, it causes the complexity of extractMin() operation to increase to O(k log kn) as compared to the complexity of O(log2n) when using binary heaps for priority queue. This allows D-ary heap to be more efficient in algorithms where decrease priority operations are more common than extractMin() operation. Example: Dijkstra’s algorithm for single source shortest path and Prim’s algorithm for minimum spanning tree
D-ary heap has better memory cache behaviour than a binary heap which allows them to run more quickly in practice, although it has a larger worst case running time of both extractMin() and delete() operation (both being O(k log kn) ).
13.5 Binomial Heap
http://www.growingwiththeweb.com/data-structures/binomial-heap/overview/
http://typeocaml.com/2015/03/17/binomial-heap/
可并堆(Mergeable Heap)也是一种抽象数据类型,它除了支持优先队列的三个基本操作(Insert, Minimum, Delete-Min),还支持一个额外的操作–合并操作.
Binomial和binary字面的差别就是binomial强调由两个部分组成,比如knife and fork就是一个Binomial. \((p+q)^n\)的系数也叫做binomial coefficient. binary强调有两个.
实际应用很少,知道就行了.
13.6 Leftish Tree
http://typeocaml.com/2015/03/12/heap-leftist-tree/
http://www.dgp.toronto.edu/people/JamesStewart/378notes/10leftist/
A “leftist tree” is an implementation of a mergeable heap.
左偏堆的合并操作的平摊时间复杂度为O(log n),而完全二叉堆为O(n).左偏堆适合基于合并操作的情形.由于左偏堆已经不是完全二叉树,因此不能用数组存储表示,需要用链接结构.
https://www.cs.usfca.edu/~galles/visualization/LeftistHeap.html
13.9 347. Top K Frequent Elements
Given a non-empty array of integers, return the k most frequent elements.
For example,
Given [1,1,1,2,2,3] and k = 2, return [1,2].
Note:
You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
Your algorithm’s time complexity must be better than \(O(n log n)\), where n is the array’s size.
https://leetcode.com/problems/top-k-frequent-elements/
这道题应该和find Kth largest element区别开来
13.9.1 Max Heap (Priority Queue)
struct Solution { // T: O(N*LogN) S: O(N)
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> counter; // 1
for(int i: nums) counter[i]++; // O(N)
priority_queue<pair<int,int>> Q;
for_each(counter.begin(), counter.end(), // O(N*LogN)
[&Q](const pair<int,int>& pr){Q.push({pr.second, pr.first});});
vector<int> r;
for(int i=0; i<k; ++i) r.push_back(Q.top().second), Q.pop(); // O(K*LogN)
return r;
}
};Performance: 1. map (52ms, 26.53%); unordered_map (32ms, 91.21%)
Complexity - T: \(O(N*LogN)\) S: \(O(N)\)
在使用priority_queue的时候,尽量使用其构造函数来初始化,常见的错误是先创建一个空的priority_queue然后一个个把元素加进去.
Actually, building a heap with repeated calls of siftDown has a complexity of \(O(n)\) whereas building it with repeated calls of siftUp has a complexity of \(O(nlogn)\).
This is due to the fact that when you use siftDown, the time taken by each call decreases with the depth of the node because these nodes are closer to the leaves. When you use siftUp, the number of swaps increases with the depth of the node because if you are at full depth, you may have to swap all the way to the root. As the number of nodes grows exponentially with the depth of the tree, using siftUp gives a more expensive algorithm.
- std::relational operators (pair) are built in STL library: http://www.cplusplus.com/reference/utility/pair/operators/
因此改进上面的方案,用priority_queue的构造函数.代码如下:
struct Solution { // T: O(N+KLogN) S: O(N)
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> counter; // 1
for(int i: nums) counter[i]++; // O(N)
auto comp=[](pair<int,int>& a,pair<int,int>& b){
return a.second<b.second;};
priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(comp)>
Q(counter.begin(), counter.end(), comp);// make_heap O(N)
vector<int> r;
for(int i=0; i<k; ++i) r.push_back(Q.top().first), Q.pop(); // O(K*LogN)
return r;
}
};Complexity - T: \(O(N+K*LogN)\) S: \(O(N)\)
13.9.2 Bucket Sort
Bucket Sort其实根本没有比较,所以可以做到线性复杂度. Bucket index is frequency, and data inside are vector of numbers.
struct Solution { // Performance: 45ms, 38%
vector<int> topKFrequent(vector<int>& nums, int k) {
int N = nums.size();
vector<int> r;
vector<vector<int>> bucket(N+1, r);//!!N+1
unordered_map<int,int> counter;
for(int i: nums) counter[i]++;
for(auto& pr: counter) bucket[pr.second].push_back(pr.first);
for(int i=N; i>=0; --i)
if(!bucket[i].empty())
for(int j: bucket[i]){
r.push_back(j);
if(--k==0) return r;
}
return r;
}
};上面这个方法bucket size初始化为nums的size,这里不够优化.我们找到最大的frequency用它来作为bucket的size可以节约不少时间和空间. 下面这个是改进版本,已经快接近最优解了:
struct Solution { // 32ms, 92.61% O(N)
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int,int> counter;
for(int i: nums) counter[i]++;
int mx=0; // get max frequency
for(auto& pr: counter) mx=max(mx, pr.second);
vector<int> r;
vector<vector<int>> bucket(mx+1, r);//create a bucket of size mx+1
for(auto& pr: counter) bucket[pr.second].push_back(pr.first);
for(int i=mx; i>=0; --i)
if(!bucket[i].empty())
for(int j: bucket[i]){
r.push_back(j);
if(--k==0) return r;
}
return r;
}
};这个思想其实就是The Algorithm Design Manual里面说的数据结构叫做bounded-height priority queue.这个前提是已经知道元素是固定的,比如股市的股票只有3000多个,字母只有26个…
Complexity - T: O(N) S: O(N)
13.9.3 Quick Selection
最优解来自于下面的方法.
struct Solution {
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> counter;
for (const auto& i : nums) ++ counter[i];
vector<pair<int, int>> p;// {-frequency, key}
for (auto& pr: counter) p.emplace_back(-pr.second, pr.first); //!!
nth_element(p.begin(), p.begin() + k - 1, p.end()); // O(N)
vector<int> r;
while(k--) r.emplace_back(p[i].second);
return r;
}
};注意这个方法返回的topK并不一定是sorted的.这就是它为什么比上面的方法更快的原因.
Performance: 29ms, 99%
Complexity - T: average O(N), worst O(N^2); S: O(N)
Note:
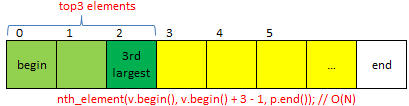
nth_element and its complexity, which is not necessarily
O(N). The algorithm used is typicallyintroselectalthough other selection algorithms with suitable average-case complexity are allowed. Refer to: https://stackoverflow.com/questions/11068429/nth-element-implementations-complexitiesvector::emplace_back
v.emplace_back(pair<int,int>(10,8))forwards a std::pair with first equals to 10 and second equals to 8 to the actual std::pair constructor for the new element. (copy constructor).v.emplace_back(10,8)is better because it forwards parameters 10 and 8 to the std::pair cosntructor for the new element and avoids creating one extra temporary object.
http://www.1point3acres.com/bbs/thread-206781-1-1.html
http://www.1point3acres.com/bbs/thread-200110-1-1.html
http://www.1point3acres.com/bbs/thread-123109-1-1.html
13.9.4 Follow up: Sorted Streaming Data
小哥想要的答案是,那个stream应该是Sorted的,所以不用map,直接count每个element的次数,再判断是否加入priorityqueue里～加油哈!
https://goo.gl/a6q3jj
http://www.1point3acres.com/bbs/thread-119909-1-1.html
你好,以下是我面试当天的代码,仅供参考 :) “1123334777…” Stream ar; ar.poll() either returns next integer or null if none left
public int[] solver(Stream ar, int k) {
if (ar == null || ar.length < k) {
return null;
}
int[] res = new int[k];
Queue<Node> minHeap = new PriorityQueue<>(k / 2, new Comparator<Node>() {
public int compare(Node a, Node b) {
return a.count - b.count;
}
});
Integer candidate = ar.poll();
int cnt = 1;
while (candidate != null) {
Integer tmp = ar.poll();
if (tmp != candidate) {
Node node = new Node((int) candidate, cnt);
if (minHeap.size() == k && minHeap.peek().count < node.count) {
minHeap.poll();
minHeap.offer(node);
} else {
minHeap.offer(node);
}
candidate = tmp;
cnt = 1;
} else {
cnt++;
}
}
int j = k - 1;
// takes O(klogk)
while (!minHeap.isEmpty()) {
res[j] = minHeap.poll().val;
j--;
}
return res;
}- How to read a growing text file in C++?
http://stackoverflow.com/questions/11757304/how-to-read-a-growing-text-file-in-c
int read_growing_file(const string& filename){
std::ifstream ifs(filename);
if (ifs.is_open()){
std::string line;
while (1){
while (std::getline(ifs, line)){
std::cout << line << "\n";
}
if (!ifs.eof()) break; // Ensure end of read was EOF.
ifs.clear();
sleep(1);
}
}
return 0;
}http://www.geeksforgeeks.org/find-the-k-most-frequent-words-from-a-file/
13.9.5 follow up: Unsorted Streaming Data
http://www.1point3acres.com/bbs/thread-204213-1-1.html
这题让设计一个程序显示前K个最大成交量的股票.
http://stackoverflow.com/questions/11209556/print-the-biggest-k-elements-in-a-given-heap-in-oklogk
https://www.quora.com/What-algorithm-is-used-for-top-k-frequent-items-in-data-streams
struct stock {
string ticker;
int volume;
};
class index_heap {
vector<stock> stocks;// heap core data
unordered_map<string, int> ticker2index;
void __swap(int x, int y) {
std::swap(ticker2index[stocks[x].ticker],
ticker2index[stocks[y].ticker]);
std::swap(stocks[x], stocks[y]);
}
// https://goo.gl/x56YT9
void __sift_up(int idx) { // iterative
if (idx >= stocks.size()) return;
stock t=stocks[idx];
while (idx > 0 && stocks[(idx-1)/2].volume < t.volume) {
stocks[idx] = stocks[(idx-1)/2], ticker2index[stocks[idx].ticker]=idx;
idx = (idx-1)/2;
}
stocks[idx] = t, ticker2index[stocks[idx].ticker]=idx;
}
void __sift_down(int idx) { // recursive
if (idx >= stocks.size()) return;
int lchild = 2 * idx + 1, rchild = 2 * idx + 2;
if (stocks.size() > rchild) {
if (stocks[lchild].volume > stocks[rchild].volume) {
if(stocks[idx].volume < stocks[lchild].volume){
__swap(idx, lchild), __sift_down(lchild);
}
} else {
if(stocks[idx].volume < stocks[rchild].volume){
__swap(idx, rchild), __sift_down(rchild);
}
}
} else if (stocks.size() > lchild) {
if(stocks[idx].volume < stocks[lchild].volume){
__swap(idx, lchild), __sift_down(lchild);
}
} else return;
}
public:
index_heap(){}
index_heap(const vector<stock>& s){
stocks=s;
for(int i=0;i<s.size();++i)
ticker2index[stocks[i].ticker]=i;
for (int tmp=(stocks.size()+1)/2; tmp>=0; tmp--)
__sift_down(tmp);
}
void push(const stock& s) {
stocks.push_back(s);
ticker2index[s.ticker] = stocks.size() - 1;
__sift_up(stocks.size() - 1);
}
void increase_volume(const string& t, int vol) {
stocks[ticker2index[t]].volume += vol;
__sift_up(ticker2index[t]);
}
void decrease_volume(const string& t, int vol) {
stocks[ticker2index[t]].volume -= vol;
__sift_down(ticker2index[t]);
}
vector<stock> topK(int k) {
vector<stock> r;
if (stocks.empty()) return r;
auto comp = [&](stock& s1, stock& s2) { return
stocks[ticker2index[s1.ticker]].volume
< stocks[ticker2index[s2.ticker]].volume; };
priority_queue<stock,vector<stock>, decltype(comp)> pq(comp);//!!
pq.push(stocks[0]);
while (k-- && !pq.empty()){
stock tmp = pq.top(); pq.pop();
r.push_back(tmp);
int lchild = 2 * ticker2index[tmp.ticker] + 1,
rchild = 2 * ticker2index[tmp.ticker] + 2;
if (lchild<stocks.size()) pq.push(stocks[lchild]);
if (rchild<stocks.size()) pq.push(stocks[rchild]);
}
return r;
}
};上面用到这个数据结构叫Index Heap, 见 Algorithms 4ed Sedgewick Page 332.
-
一个交易所的股票的数量大概不过几千个.Nasdaq的股票只有3000多.
stocks可以预先分配空间.
-
__sift_up和__sift_down可以用iterative或者recursive的写法,recursive要容易写些.
-
实际情况volume不可能会减少,这里为了算法的完整性,把
decrease_volume也写了.
因为股票的数量有限,所以这个程序不会占用多少空间.时间复杂度也可以接受.完全可以用在生产环境.
但是如果不是股票,而是IP地址,上面的方法就还不够了.
IPv4一共有4G个地址: \(2^{32}=4 294 967 296\)
IPV4一些特殊的IP地址:
- 127.x.x.x给本地网地址使用.
- 224.x.x.x为多播地址段.
- 255.255.255.255为通用的广播地址.
- 10.x.x.x,172.16.x.x至172.31.x.x 和192.168.x.x供本地网使用.
实际可以用的IPV4地址很少,已经远远不够使用了.
13.9.6 follow up: Huge Unsorted Data
http://www.1point3acres.com/bbs/thread-159538-1-1.html
如果真的是system design的话,说把所有信息都放在一个heap或者map里面的这种解决方案会让面试官觉得你缺少实际的工程经验,除非这个面试官也是从网上道听途说这样一个题目的junior engineer.
作为一个严肃的可以操作的系统,你需要考虑这么几个方面:
1. 数据持久化(persistent) (历史数据的查询,以及服务器crash之后的重新恢复)
2. 可扩展性(extensibility)
3. 实时性(realtime) 与误差的trade off
4. 稳定性(stability)
5. 可用性(availability)
6. scalability - 这点存疑一下,因为需求并不明确先考虑最原始但是可用的方法以及其中的几个关键点.
考虑到availability和stability,首先你不能有single point of failure.你要有一个分布式的队列服务,即使你的后端服务器crash,也不会丢失现在正在产生的数据.在你的服务器重新上线之后,可以继续处理在队列中累积的数据.这里的队列服务可用kafka (https://kafka.apache.org/) 或者 kinesis (https://aws.amazon.com/kinesis/streams/).
persistent layer,因为我们这里先讲最原始的办法,我们只考虑用relational database.把所有data都存在一个地方显然是比较蠢的办法.比较理性的做法是按照IP hash,然后无论你是partition也好,还是干脆就分不同的table也好(因为IP的key空间是钉死的),把他们分到不同的服务器上去均衡负载.你的database server要有备份.要有slave,当master下线时slave仍然可以提供只读服务.
你的服务层要有redundancy, 一台机器因故下线了还可以有其它的顶住.
查询时从每个database查询top 10然后一个heap来merge result就好了.
上面这个解决方案是基本可行的,基于ip address的空间并不是很大,Oracle的db可以支持上G的table问题不大,你partition个四五次就还可以支持.
当然也有问题,比如说,写操作会很频繁,我们需要cache多次访问记录然后batch update,这里就涉及到了稳定性问题,因为你在什么地方cache这个中间结果,什么地方就有可能出问题,出了问题你就会丢数据.而在cache和真正写之间,也会有accuracy的问题.
所以如果要处理非常大的数据两,需要稍微fancy一点的解决方案.
比如说后端数据库,可以换用任何一种key-value store,或者推到极致,我们只需要raw访问记录.
然后将访问记录持久化到我们的分布式文件系统中,比如HDFS.这里能解决的是后端数据库的scale问题.我们需要周期性地在这个文件系统上跑Map-Reduce job,以获得更新的记录.然而要注意的是MR是非常慢的一个过程,通过MR sort算出来的结果往往是几个小时之前的了.Anyway到这个point,我们能够获得一个几小时前的访问频率的排名.
然后近几个小时中的访问频率,我们可以用apache storm (http://storm.apache.org/) 来做stream处理,在服务层和之前MR预处理过的结果combine起来(一共才4G个条目,这里因为我们所有的历史结果都已经persistent,所以内存处理方法是可行的——可以用数台机器,每台返回其上的前10,最后combine),得到最终的结果.
问: 给你一个海量的日志数据,提取出某日访问网站次数最多的IP地址.
答: 将日志文件划分成适度大小的M份存放到处理节点.每个map节点所完成的工作:统计访问的ip的出现频度(比较像统计词频,使用字典树),并完成相同ip的合并(combine). map节点将其计算的中间结果partition到R个区域,并告知master存储位置,所有map节点工作完成之后,reduce节点首先读入数据,然后以中间结果的key排序,对于相同key的中间结果调用用户的reduce函数,输出. 扫描reduce节点输出的R个文件一遍,可获得访问网站度次数最多的ip.
面试官角度:
该问题是经典的Map-Reduce问题.一般除了问最常访问,还可能会问最常访问的K个IP.一般来说,遇到这个问题要先回答Map-Reduce的解法.因为这是最常见的解法也是一般面试官的考点.
13.10 499. Word Count (Map Reduce)
Using map reduce to count word frequency.
https://hadoop.apache.org/docs/r1.2.1/mapred_tutorial.html#Example%3A+WordCount+v1.0
Example
chunk1: "Google Bye GoodBye Hadoop code"
chunk2: "lintcode code Bye"Get MapReduce result:
Bye: 2
GoodBye: 1
Google: 1
Hadoop: 1
code: 2
lintcode: 1http://www.lintcode.com/en/problem/word-count-map-reduce/
/**
* Definition of OutputCollector:
* class OutputCollector<K, V> {
* public void collect(K key, V value);
* // Adds a key/value pair to the output buffer
* }
*/
public class WordCount {
public static class Map {
public void map(String key, String value, OutputCollector<String, Integer> output) {
// Write your code here
// Output the results into output buffer.
// Ps. output.collect(String key, int value);
String ls[] = value.split(" ");
for(String w: ls)
output.collect(w,1);
}
}
public static class Reduce {
public void reduce(String key, Iterator<Integer> values,
OutputCollector<String, Integer> output) {
// Write your code here
// Output the results into output buffer.
// Ps. output.collect(String key, int value);
int sum=0;
while(values.hasNext())
sum += values.next().intValue();
output.collect(key, sum);
}
}
}
-
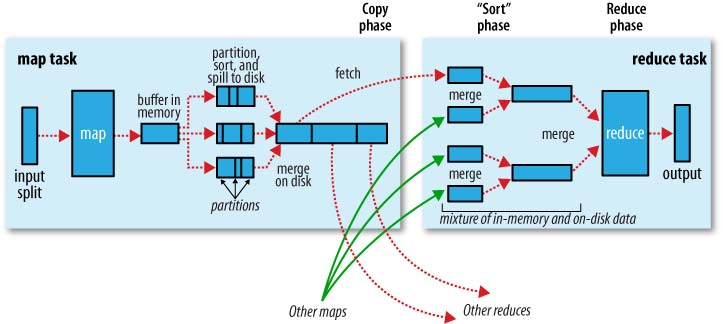
Hadoop的MapReduce阶段为什么要进行排序呢,这样的排序对后续操作有什么好处么?
https://www.zhihu.com/question/35999547
MR在reduce阶段需要分组,将key相同的放在一起进行规约,为了达到该目的,有两种算法:hashmap和sort,前者太耗内存,而排序通过外排可对任意数据量分组,只要磁盘够大就行.map端排序是为了减轻reduce端排序的压力.在spark中,除了sort的方法,也提供hashmap,用户可配置,毕竟sort开销太大了.
Shuffle好理解,上面已经解释了原因,Sort又耗时又没有意义(因为对于Reduce而言,什么顺序都不会影响结果的),为什么要Sort之后才传给Reduce呢? 经过多方查证,原来在Google的MapReduce论文里就是这样定义的,主要是Google在Reduce之后存储,要是有序的话,查询会更方便些.Hadoop在实现Google的MapReduce论文时,也实现了Sort阶段.
http://stackoverflow.com/questions/11746311/where-is-sort-used-in-mapreduce-phase-and-why
It is there, because sorting is a neat trick to group your keys. Of course, if your job or algorithm does not need any order of your keys, then you will be faster to group by some hashing trick.
We guarantee that within a given partition, the intermediate key/value pairs are processed in increasing key order. This ordering guarantee makes it easy to generate a sorted output file per partition, which is useful when the output file format needs to support efficient random access lookups by key, or users of the output find it convenient to have the data sorted.
So it was more a convenience decision to support sort, but not to inherently only allow sort to group keys.
你说的应该是MapReduce计算框架过程中的sort phase发生sort有两个地方 一个是在map side发生在spill后 partition前一个是在reduce side 发生在copy后 reduce前那么问题来了 这个sort有什么好处呢答案 没什么好处一开始被这个问题咯噔了一下后来一想 发现其实问反了应该说 MapReduce这个框架就是为了分布式计算 然而计算最basic的就是排序所以说MapReduce最初衷的目的就是为了大数据排序而设计也不会有什么问题08年 这个框架排T等级的数据是最快的 记得有个奖所以这么说吧不是sort对后续操作有何好处 而是这个sort为许多应用和后续应用开发带来很多好处 试想分布式计算框架不提供排序 要你自己排 真是哇哇叫 谁还用.
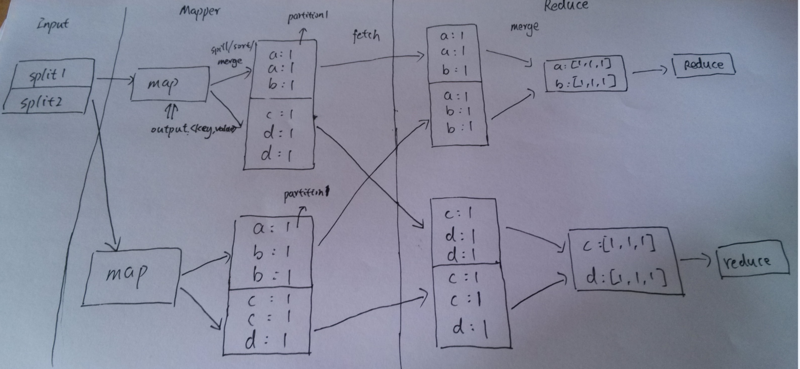
Detailed Hadoop MapReduce data flow
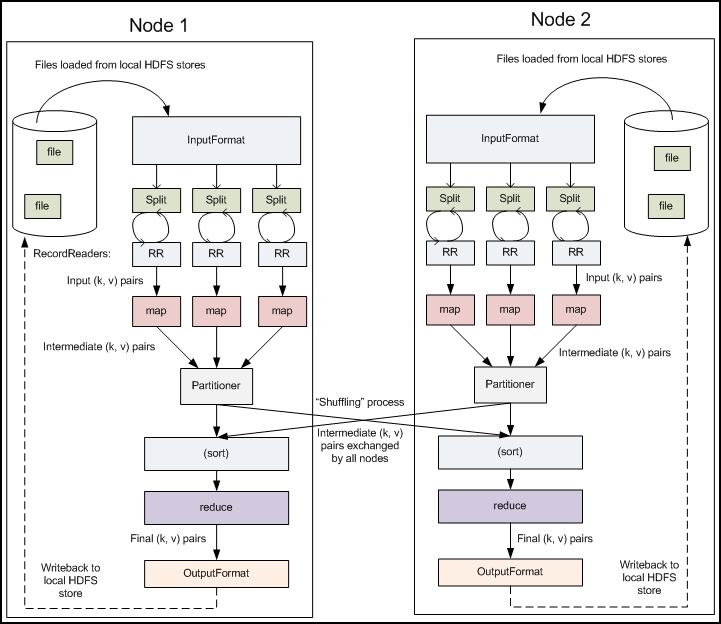
https://developer.yahoo.com/hadoop/tutorial/module4.html#dataflow
如果面试官水平高一点,要进一步问你有没有其他解法的话,该问题有很多概率算法.能够在极少的空间复杂度内,扫描一遍log即可得到Top k Frequent Items(在一定的概率内).有兴趣的读者,可以搜搜Sticky Sampling,Lossy Counting这两个算法.
Lossy Count Algorithm: This algorithm finds huge application in computations where data takes the form of a continuous data stream instead of a finite data set, for e.g. network traffic measurements, web server logs, clickstreams.
https://micvog.com/2015/07/18/frequency-counting-algorithms-over-data-streams/
In computer science, streaming algorithms are algorithms for processing data streams in which the input is presented as a sequence of items and can be examined in only a few passes (typically just one). These algorithms have limited memory available to them (much less than the input size) and also limited processing time per item.
https://en.wikipedia.org/wiki/Streaming_algorithm#Some_streaming_problems
13.11 Lossy Counting
http://www.jiuzhang.com/qa/109/
实时输出最近的一个小时内访问频率最高的10个IP
1.首先看到实时,就一定不能靠挖掘LOG的方式去更新数据,等log落到硬盘上再读回来至少做了两次IO,黄花菜都凉了.
2.所以一定要在内存中存数据,这个找出10个最大值,可能经典算法就是HEAP(这里因为涉及更新,以IP为key更新频率,所以需要priority queue, 其实就是加了索引的HEAP,查询O(1),符合我们实时的要求,更新O(logn)). 但是HEAP的问题是locality 极差,如果不能完全放入内存,PAGE-IN/PAGE-OUT太多,无法接受. 那么我们算算能不能全在内存,算这个网站的一天访问的总人数是10M(为什么算一天,因为一般网站都是夜里挖掘log,第二天就可以做个新的起始数据).因为不同DEVICE或者手机蜂窝网,就算每个人有4个IP,一个IP加频率,一条ITEM8bytes.一共40M*8=320M. 要是面试官不通人情就再乘3,算是高峰日(比如周日),我觉得还是可以存进去的.
3.如果链接来了,更新这个PQ,各种+1,但是不能忘了一个问题,就是我们要前一小时的,怎么解决过期的问题呢?这时候log可以派上用场,有背景PROCESS,挖掘log,挖过期那一秒的log,然后发-x的信息去更新PQ,所以这个系统的链接和过期其实并没有什么区别,一种是+,一种是-,我们在PQ只需要接收这个变化量. 但是,这个系统要想WORK,必须要确保挖掘时间跟的上,如果你用2S,挖掘完1S的数据,那就GG了.算一下能否做到:10W*16byte=1.6M.按10的6次方的原则,可能需要两个机器,如果是两个SERVER加上LOAD BALANCE,那再好不过,挖自己的LOG就好.如果不是这样,也可以简单的分配一下,比如ID为奇数的给一个机器,偶数的另一个(多机同理,if(id%x==y)),保证一秒能挖掘完一秒产生的LOG.
4.但是,如果就这样,找出前一百,一千也是这个做法,如果不利用TOP10这个10,显得我们逼格不高. 这个问题有一个特点就是,大多数情况,现在的前十,下一秒很可能不变,唯一变化可能是第十名,所以我们可以存更小的一个PQ,比如32个(cache hit 杠杠的),我们管这个叫小HEAP,之前说的那个叫大HEAP.两者同时接受因为链接和LOG而来的+和-.并且,所有的读取都走这个小HEAP,因为他小,所以速度应该没得说.但是,一切皆有可能,中国队也进过世界杯,万一33杀进32怎么办,更新小HEAP就可以了.这个说白了就是一个CACHE,小HEAP小而快,大HEAP大而全,满足一定条件就更新.保证速度,又不失准确性.
5.挂了咋办? 定期CHECKPOINT大HEAP到硬盘,RECOVER的时候,读这个加上从这个PROCESS挂掉时间算起,之后LOG中发生的事. 如果不这样,我们需要再次挖一小时内的LOG才能把这个大HEAP建立起来,那就默默无语两眼泪了..
优点:如果完全依赖于LOG,去更新PQ,可能实时性会差,因为正向的LOG需要等他写完,两次IO,然后再算上挖掘的时间….如果读一小时前的LOG,我们会直接在内存里准备好,实时性比较高. 缺点: 1)不准(虽然比实时挖LOG强),小HEAP和大HEAP也不是consistent的,但貌似如果要速度,都要牺牲consistent.而且,这个微小的准确性差异的意义有多大呢?如果算上用户的RTT,等数据给了他,他看到的也是延迟的结果. 2)我不知道更新大HEAP会不会做到实时,虽然他都在内存里,我假设10W/s次更新是能HOLD住的.但是因为更新可能会锁(不要锁PQ,那就土了,只锁ITEM,减小锁的粒度),可能速度不达标.觉得老师上次给看的排队是一种解决办法,另一种可能是多机,根据IP分配给不同的机器,所以每个机器存的大HEAP理论上小了一倍小HEAP不变,最后读数据的时候,从所有机器的小HEAP里读取,MERGE一下(同MERGESORT的MERGE).然后给出结果,应该可以应付.
暴力点的解法: 假设有 1亿个IPs, 有个超级服务器,建立以个一亿 elements的 max heap. 每次访问, 纪录下IP, update its count int the max heap. 每次要统计的时候, get top 10 from the heap.
显然,前面的方法是有资源上和方法上的严重缺陷的,但是提供个思路也挺好的. 比如内存的大小限制, concurrent writes on the giant heap, 都是大问题.
我其实可以做成一个分布式的heap结构,比如用 100台服务器, 每台都存着 IP-> frequency count, 大约有 1亿／100 ＝ 1百万 IPs. 同时每台有 10-size的heap, top 10 可以cache着. 新的IPs可以不断的加进来,加到每台服务器上. 每当每台服务器的 top 10 变化的时候, update top 10, 而且 cache, 并且通知主服务器:我的数据变了.
当我们需要real time 统计top 10的总IPs的时候.master服务器就去这100台servers去取, 但是不是向所有的都去取, 只向那些通知数据已变的服务器去取. 这样会减少网络流, 而且是需要统计的时候才去取数据, 不需要的时候就老实呆着.这样, 很快就能从底下的服务器取得最新的 每台的top 10. 最后汇总一下,得到 最终的 top 10 就行了.
抛砖引玉, 欢迎指正.
我专门针对这个问题做过论文的研究.有很多的方法可以解决这个问题.得看是否允许损失精度.
一般来说,实际的运用,都是允许损失精度的,也就是有一定概率找得不准,但是这个概率很低.
有这么几个算法可以解决这个问题,有兴趣的同学搜一下论文,基本都是O(k)空间和realtime的.k是你要找top-k的.
Lossy Counting
Space Saving
Sticky Sampling
Efficient Counting
Hash Count 还有很多这方面的算法,我没举完.我比较喜欢的是Space-Saving和Hash Count(还有一个算法是Hash Count 2),以Hash Count算法为例子.这个做法特别简单就是用一个Hash表,但是不存Key,只存value(一个数组就搞定了),然后每个key过来,我就算出对应的hashcode是什么(一个index呗),去hash表里找对应的位置,count++.这个方法听起来就是,如果两个key有同样的hashcode,然后count就会被叠加到一起,但是实际上你要找的top-k的k是很小的,比如10,所以基本上对最后结果有影响的概率也是很小的.所以这种方法是我认为最实用的方法.
有兴趣的同学可以搜索“Top-k Frequently Elements”或者类似的关键词来查找相关的论文.
to 张老师 “如果要做到实时的话,还有一个窍诀,在当前时刻重放之前一个小时这个时刻发生的log,但是要-1” 是loosy counting 思想吗,这样的话要把一小时前的log也都存起来了吧?
是的,记录之前1个小时内的log
应该是存在内存的time queue里面.
还发现一个facebook的TopK库: http://facebook.github.io/jcommon/stats/jacoco/com.facebook.stats.topk/index.html
13.11.1 Storm for TopN
Storm常见模式——求TOP N
http://www.cnblogs.com/panfeng412/archive/2012/06/16/storm-common-patterns-of-streaming-top-n.html
在多台机器上并行的运行多个Bolt,每个Bolt负责一部分数据的TOP N计算,然后再有一个全局的Bolt来合并这些机器上计算出来的TOP N结果,合并后得到最终全局的TOP N结果.
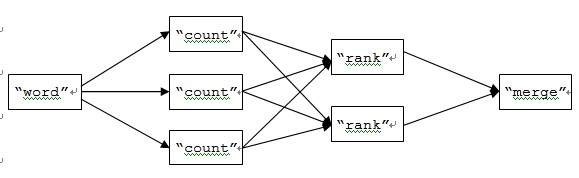
13.12 xxx_heap in STL
Does the STL provide a heap container class? No, it doesn’t. Why not? Well, to have a separate heap container class would be redundant since a heap is just a vector in which the values have a certain arrangement. What it does have, instead, is some algorithms especially designed for working with vectors that are heaps, or that we want to be heaps.
C++ has a replacement for heap: priority_queue, which cannot meet requirement in many cases. priority_queue has no update, no erase methods.
Although there is no sift up and sift down, we can use push_heap() to do the same!
A toy implementation, using STL <algorithm> XXX_heap function, of a dynamic heap is:
struct myheap {
vector<int> d;
myheap(const vector<int>& _d) {
d = _d;
make_heap(d.begin(), d.end());
}
void push(int i) {
d.push_back(i); // O(LogN)
push_heap(d.begin(), d.end());
}
int pop() {
pop_heap(d.begin(), d.end()); // O(LogN)
int t = d.back(); d.pop_back();
return t;
}
void erase(int n) { // O(N)
update(n, INT_MAX);
pop();
}
void update(int old_, int new_) { // O(N+LogN) = O(N)
int i = 0;
for (; i < d.size(); ++i) // O(N)
if (d[i] == old_) { d[i] = new_; break; }
push_heap(d.begin(),d.begin()+i+1);// the same like sift up/down
}
int size() { return d.size(); }
};用STL的内置XXX_heap函数只能把heap到这个程度了.update和erase都是\(O(N)\).
如果用一个map把data和index对应起来,就可以降为\(O(LogN)\).
但是push_heap和pop_heap将不能使用,用为index要变,而这两个函数没办法改变map.有人把这个map和heap结合的数据结构叫做index heap,就是对heap里面的data做了index,可以迅速找到以便更新或者删除.麻烦的是需要自己实现相应的push_heap, pop_heap, make_heap函数.所以手写heap这种简单的数据结构应该要很流畅的完成才行.
https://kartikkukreja.wordpress.com/2013/05/28/indexed-min-priority-queue-c-implementation/
13.13 630. Course Schedule III
https://leetcode.com/problems/course-schedule-iii/
https://leetcode.com/articles/course-schedule-iii/
class Solution {
public:
int scheduleCourse(vector<vector<int>>& courses) {
sort(courses.begin(), courses.end(), [](vector<int>& l,vector<int>& r){
return l[1]<r[1];
});
priority_queue<int> q;
int time=0;
for(auto c: courses){
if(time+c[0] <= c[1])
q.push(c[0]), time+=c[0];
else if(!q.empty() && q.top()>c[0])
time+=c[0]-q.top(), q.pop(), q.push(c[0]);
}
return q.size();
}
};First, we sort courses by the end date, this way, when we’re iterating through the courses, we can switch out any previous course with the current one without worrying about end date. 想通了这一点这道题就明白了一大半.
13.14 K-Way Merging
13.15 774. Minimize Max Distance to Gas Station
https://leetcode.com/contest/weekly-contest-69/problems/minimize-max-distance-to-gas-station/
On a horizontal number line, we have gas stations at positions stations[0], stations[1], …, stations[N-1], where N = stations.length.
Now, we add K more gas stations so that D, the maximum distance between adjacent gas stations, is minimized.
Return the smallest possible value of D.
Example:
Input: stations = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], K = 9
Output: 0.500000
Note:
stations.length will be an integer in range [10, 2000].
stations[i] will be an integer in range [0, 10^8].
K will be an integer in range [1, 10^6].
Answers within 10^-6 of the true value will be accepted as correct.13.15.1 Heap
Though TLE, a good idea it is.
struct interval{
double l;
int n;
double g;
interval(double d):l(d),n(1),g(l){}
};
struct comp{
bool operator()(interval& x, interval& y){
return x.g < y.g;
}
};
class Solution { // (N+K*LogN)
public:
double minmaxGasDist(vector<int>& v, int K) {
priority_queue<interval,vector<interval>,comp> pq;
for(int i=0;i<(int)v.size()-1;++i){ // N
double ds=(double)(v[i+1])-v[i];
pq.emplace(ds);
}
while(K--){ // K
auto tp=pq.top();
pq.pop();
tp.n+=1, tp.g=tp.l/tp.n;
pq.push(tp);
}
auto r=pq.top();
return r.g;
}
};13.15.2 Binary Search
https://codereview.stackexchange.com/questions/155102/minimize-max-distance-of-gas-station
Calculate lower and upper bound of gas station distance (lower bound 1, higher bound is current max distance between two existing gas stations)
Do a binary search for lower bound and higher bound, to see if we can fit with k gas stations. If we can fit, then try to lower higher bound of binary search. If we cannot fit, then try to higher lower bound of binary search
At the end, the number is minimal of max distance between gas stations
class Solution { // O(?*N)
public:
double minmaxGasDist(vector<int>& v, int K) {
adjacent_difference(v.begin(), v.end(), v.begin());
v.erase(v.begin());
int mx=*max_element(v.begin(), v.end());
double h=0, t=(double)mx;
while(t-h>1e-9){ // O(?)
double m=h+(t-h)/2.0;
long long required=0;
for(int i: v) // O(N)
required+=ceil(i/m)-1;
if(required>K){
h=m;
}else{
t=m;
}
}
return t;
}
};13.16 169. Majority Element
https://leetcode.com/problems/majority-element/
Given an array of size n, find the majority element. The majority element is the element that appears more than floor(n/2) times.
You may assume that the array is non-empty and the majority element always exist in the array.
struct Solution {
int majorityElement(vector<int>& nums) {
int c = 0, r = 0;
for (int i: nums)
if (c == 0)
r=i, c=1; // 1. initialization
else
(r==i) ? c++: c--; // 2. logic
return r;
}
};Another way but same time complexity:
class Solution {
public:
int majorityElement(vector<int> &num) {
int majorityIndex = 0, count = 1;
for (int i = 1; i < num.size(); i++) {
(num[majorityIndex] == num[i]) ? count++ : count--;
if (count == 0) {
majorityIndex = i;
count = 1;
}
}
return num[majorityIndex];
}
};Acutally, the majority element may not exist in all cases. Majority vote is the vote having number greater than sum of all the rest. For example, if everybody votes to himself, there will be no majority vote.
Refer to: http://rasbt.github.io/mlxtend/user_guide/classifier/EnsembleVoteClassifier/
编程之美里面在解决了这个问题之后,提出了一个扩展问题,就是说如何找出发帖总数目大于等于1/K的ID.
int frequent_element(vector<int> nums,int k) {
map<int,int> counter;
for(int e: nums){
if(counter.count(e)){
counter[e]++;
}else if(counter.size()<k-1){
counter[e]=1;
}else{// remove element from a map in while loop
auto it=counter.begin();
while(it!=counter.end()){
counter[it->first]--;
if(counter[it->first]){
it++;
}else it=counter.erase(it); ////
}
}
}
// find the key in counter with max value and return
// ...
} How to remove from a map while iterating it: http://bit.ly/2xvXPu6 转自: http://blog.csdn.net/dm_ustc/article/details/45895851
13.17 229. Majority Element II
Given an integer array of size n, find all elements that appear more than ⌊ n/3 ⌋ times. The algorithm should run in linear time and in O(1) space.
https://leetcode.com/problems/majority-element-ii/
这道题让我们求出现次数大于n/3的众数,而且限定了时间和空间复杂度,那么就不能排序,也不能使用哈希表,这么苛刻的限制条件只有一种方法能解了,那就是摩尔投票法 Moore Voting,这种方法在之前那道题Majority Element 求众数中也使用了.题目中给了一条很重要的提示,让我们先考虑可能会有多少个众数,经过举了很多例子分析得出,任意一个数组出现次数大于n/3的众数最多有两个,具体的证明我就不会了,我也不是数学专业的.那么有了这个信息,我们使用投票法的核心是找出两个候选众数进行投票,需要两遍遍历,第一遍历找出两个候选众数,第二遍遍历重新投票验证这两个候选众数是否为众数即可,选候选众数方法和前面那篇Majority Element 求众数一样,由于之前那题题目中__限定了一定会有众数存在__,故而省略了验证候选众数的步骤,这道题却没有这种限定,即满足要求的众数可能不存在,所以要有验证.
http://www.cnblogs.com/grandyang/p/4606822.html
class Solution {
public:
vector<int> majorityElement(vector<int>& nums) {
vector<int> res;
int m = 0, n = 0, cm = 0, cn = 0;
for (auto &a : nums) {
if (a == m) ++cm;
else if (a ==n) ++cn;
else if (cm == 0) m = a, cm = 1;
else if (cn == 0) n = a, cn = 1;
else --cm, --cn;
}
cm = cn = 0;
for (auto &a : nums) {
if (a == m) ++cm;
else if (a == n) ++cn;
}
if (cm > nums.size() / 3) res.push_back(m);
if (cn > nums.size() / 3) res.push_back(n);
return res;
}
};13.18 295. Find Median from Data Stream
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value. Examples:
[2,3,4] , the median is 3
[2,3], the median is (2 + 3) / 2 = 2.5Design a data structure that supports the following two operations:
void addNum(int num) - Add a integer number from the data stream to the data structure.
double findMedian() - Return the median of all elements so far.
For example:
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2https://leetcode.com/problems/find-median-from-data-stream/
在Data stream中找到median.这道题是Heap的经典应用,需要同时维护一个最大堆和一个最小堆, 最大堆和最小堆的size <= 当前数字count / 2.见到有些朋友用了构建BST来做,这样减少了几次O(logn)的操作,速度会更快.
http://www.cnblogs.com/yrbbest/p/5044819.html
class MedianFinder {
Queue<Integer> minPQ = new PriorityQueue<>();
Queue<Integer> maxPQ = new PriorityQueue<>(10, (Integer i1, Integer i2) -> i2 - i1);
// Adds a number into the data structure.
public void addNum(int num) {
minPQ.offer(num);
maxPQ.offer(minPQ.poll());
if (minPQ.size() < maxPQ.size()) minPQ.offer(maxPQ.poll());
}
// Returns the median of current data stream
public double findMedian() {
if (minPQ.size() == maxPQ.size()) return (minPQ.peek() + maxPQ.peek()) / 2.0;
return minPQ.peek();
}
};LeetCode Questions
23 Merge k Sorted Lists 25.8% Hard
218 The Skyline Problem 25.4% Hard
347 Top K Frequent Elements 45.7% Medium
215 Kth Largest Element in an Array 37.3% Medium
264 Ugly Number II 31.4% Medium
295 Find Median from Data Stream 23.2% Hard
239 Sliding Window Maximum 31.3% Hard
451 Sort Characters By Frequency 50.7% Medium
253 Meeting Rooms II 38.1% Medium
378 Kth Smallest Element in a Sorted Matrix 43.1% Medium
313 Super Ugly Number 37.0% Medium
373 Find K Pairs with Smallest Sums 29.7% Medium
407 Trapping Rain Water II 35.2% Hard
355 Design Twitter 24.3% Medium
358 Rearrange String k Distance Apart 31.7% Hard
https://www.geeksforgeeks.org/check-if-a-given-binary-tree-is-heap/
https://www.geeksforgeeks.org/how-to-check-if-a-given-array-represents-a-binary-heap/
CLRS Heap Solutions: https://goo.gl/D5aSdW