Chapter 17 Trie and Suffix Tree
\(LCS_e\)
\(LCS_u\)
https://en.wikipedia.org/wiki/Suffix_array
https://en.wikipedia.org/wiki/LCP_array
Longest Common Prefix => Suffix Tree
Longest Common Prefix Suffix => KMP
Longest Common Substring (DP - \(O(N^2)\))
http://www.devhui.com/2015/04/21/Longest-Common-Substring/
- String Hash
http://blog.csdn.net/asdfgh0308/article/details/38847657
17.1 Trie (Prefix Tree)
Advantages of tries:
- Predictable O(k) lookup time where k is the size of the key
- Lookup can take less than k time if it’s not there
- Supports
ordered traversal, supportstart_with!! - No need for a hash function
- Deletion is straightforward
- 如何克服字典树(Trie Tree)的缺点?字典树的缺点是内存消耗非常大,有什么方法能克服它的这个缺点?
https://www.zhihu.com/question/30736334 常用的做法是用double array trie 取代朴素的trie能节省下大量内存空间,但未加修改的double array结构,大量插入时会产生大量的relocate操作,插入性能低下,最近看到叫cedar的double array改进方法.http://www.tkl.iis.u-tokyo.ac.jp/~ynaga/cedar/ 插入和删除性能已经和朴素的trie差不多了.其主要思想是建立空闲节点的索引,减少relocate和寻找可用节点的代价.官方的实现是C++版本的,有和很多常见和不常见的key-value数据结构对比的benchmark.结果上看性能确实很可观.有兴趣可以读下源码.最近在github上发现开始有用go在cedar结构上实现ahocorasick. 均衡了AC自动机的内存占用.http://github.com/iohub/Ahocorasick.
Trie的设计非常灵活,根据需要有不用的设计,非常适合面试的时候考察数据结构.这也是为什么STL里面没有Trie的原因吧.
The trie node definition could be the following.
Regular trie node:
struct node{
bool k=false;// k represent the end of a string
node *n[26]={};// Use index to represent the current char, n mean next
};To get frequency of each word:
But if you only want to query start_with, you can also use a hashmap unordered_map<string, vector<string>> trie. See  matrix.html#word-squares.
matrix.html#word-squares.
17.2 208. Implement Trie (Prefix Tree)
Implement a trie with insert, search, and startsWith methods.
Note: You may assume that all inputs are consist of lowercase letters a-z.
 https://leetcode.com/problems/implement-trie-prefix-tree/description/
https://leetcode.com/problems/implement-trie-prefix-tree/description/
struct node{
bool k=false;
node* nx[26]={};
};
class Trie {
node* r; // Root of the Trie
public:
/** Initialize your data structure here. */
Trie() {
r = new node();
}
/** Inserts a word into the trie. */
void insert(string word) {
node* cur=r;
for(char c: word){
if(cur->nx[c-'a']==0) cur->nx[c-'a'] = new node();
cur=cur->nx[c-'a'];
}
cur->k=true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
auto cur=r;
for(char c: word){
if(cur->nx[c-'a']==0) return false;
cur=cur->nx[c-'a'];
}
return cur->k;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
auto cur=r;
for(char c: prefix){
if(cur->nx[c-'a']==0) return false;
cur=cur->nx[c-'a'];
}
return true;
}
// one extra function
vector<string> get_words_start_with(const string& s) {
vector<string> re;
node* cur = r;
for (char c : s) {
if (cur == 0 || cur->n[ix(c)] == 0) return re;
cur = cur->n[ix(c)];
}
_getwords(cur, re, s); // a DFS function
return re;
}
private:
void _getwords(node* no, vector<string>& re, const string& prefix) {
if (no->k) re.push_back(prefix); // cherry pick at the end
for (int i = 0; i<26; i++)
if (no->n[i])
_getwords(no->n[i], re, prefix + (char)('a' + i));
}
};17.2.1 PATRICIA Trie
Implementation of a PATRICIA Trie (Practical Algorithm to Retrieve Information Coded in Alphanumeric). A PATRICIA Trie is a compressed Trie. Instead of storing all data at the edges of the Trie (and having empty internal nodes), PATRICIA stores data in every node. This allows for very efficient traversal, insert, delete, predecessor, successor, prefix, range, and select(Object) operations. All operations are performed at worst in O(K) time, where K is the number of bits in the largest item in the tree. In practice, operations actually take O(A(K)) time, where A(K) is the average number of bits of all items in the tree.
Most importantly, PATRICIA requires very few comparisons to keys while doing any operation. While performing a lookup, each comparison (at most K of them, described above) will perform a single bit comparison against the given key, instead of comparing the entire key to another key.
The Trie can return operations in lexicographical order using the ‘prefixMap’, ‘submap’, or ‘iterator’ methods. The Trie can also scan for items that are ‘bitwise’ (using an XOR metric) by the ‘select’ method. Bitwise closeness is determined by the KeyAnalyzer returning true or false for a bit being set or not in a given key.
This PATRICIA Trie supports both variable length & fixed length keys. Some methods, such as prefixMap(Object) are suited only to variable length keys.
http://www.cse.cuhk.edu.hk/~taoyf/course/wst540/notes/lec10.pdf
https://cw.fel.cvut.cz/wiki/_media/courses/a4m33pal/paska13trie.pdf
http://theoryofprogramming.com/2016/11/15/compressed-trie-tree/
https://www.coursera.org/learn/algorithms-on-strings/home/welcome
https://leetcode.com/articles/implement-trie-prefix-tree/
Trie for english words is basically a 26-ary tree; Trie for numeric letters is a 10-ary tree.
Implementation 1:
 https://leetcode.com/problems/implement-trie-prefix-tree/
https://leetcode.com/problems/implement-trie-prefix-tree/
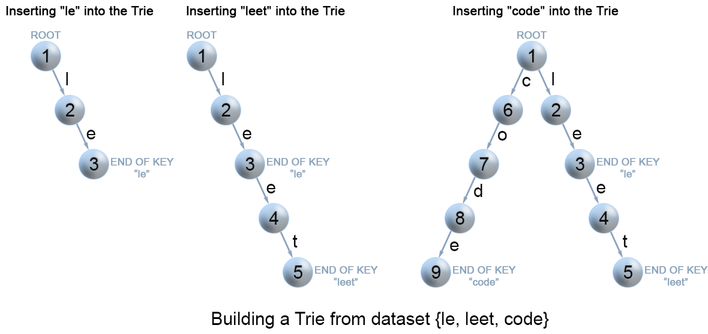
The following is one of the implementations:
struct node{
bool k=false;// k represent the end of a string
node *n[26]={};// Use index to represent the current char, n mean next
};
#define ix(x) (x-'a')
struct trie{
trie(){ r = new node(); }
void insert(const string& s){
node* cur=r;
for(char c: s){
if(cur->n[ix(c)]==0) cur->n[ix(c)] = new node();
cur = cur->n[ix(c)];
}
cur->k=true;
}
bool search(const string& s){ return _search(s,0); }
bool start_with(const string& s){ return _search(s,1);}
private:
bool _search(const string& s, bool partial){// along the way to search, all nodes are not null.
node* cur=r;
for(char c:s){
if(cur==0 || cur[ix(c)]==0) return false;
cur = cur[ix(c)];
}
return partial ? true : cur->k ;
}
node* r; // root
};
The error prone part is insert. If the cell is not null, you should not create new node. The tree ended at an empty node and the \(k\) is true for the empty node.
Trie has startsWith whcih hashtable doesn’t have.
Other Methods:
//vector<string> start_with(const string& s){}
//int count_prefix(const string& s){}
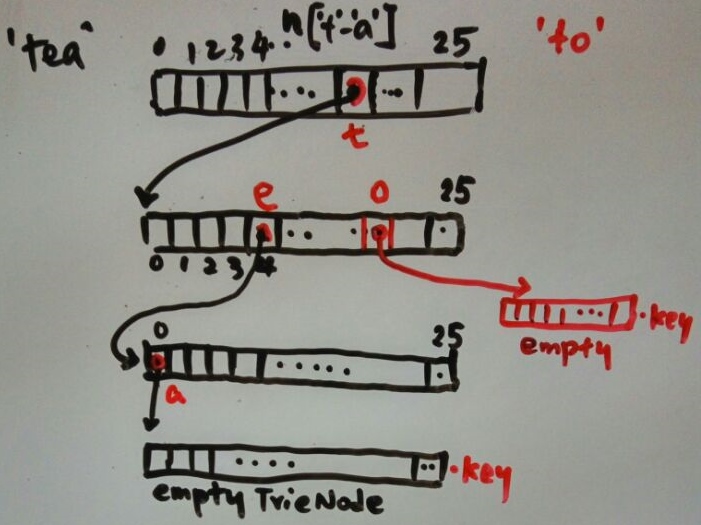
//vector<string> get_words(){}Optimization - Save space using double array
The disadvantage of trie implementation 1 is it takes too much memory.
http://linux.thai.net/~thep/datrie/datrie.html
Application
http://www.allenlipeng47.com/blog/index.php/2016/03/15/palindrome-pairs/
17.3 211. Add and Search Word - Data structure design
Design a data structure that supports the following two operations:
void addWord(word)
bool search(word)search(word) can search a literal word or a regular expression string containing only letters a-z or .. A . means it can represent any one letter.
For example:
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> trueNote: You may assume that all words are consist of lowercase letters a-z.
 https://leetcode.com/problems/add-and-search-word-data-structure-design/
https://leetcode.com/problems/add-and-search-word-data-structure-design/
https://www.topcoder.com/community/data-science/data-science-tutorials/using-tries/
这里只要搜索不要求词频什么的,就选第一种定义.稍微难点的地方是对wild card matching(“.”)的处理,需要用到递归.
struct node{
node* nt[26]={0};
bool k=false;
};
class WordDictionary {
node* r;
public:
WordDictionary() { r=new node(); }
void addWord(string word) {
auto t=r;
for(char c: word){
if(t->nt[c-'a']==0) t->nt[c-'a']=new node();
t=t->nt[c-'a'];
}
t->k=true;
}
bool search(string word) { return rec(r,word,0); }
bool rec(node* p, string &w, int i){
if(i==w.size()) return p->k;// end of string
if(w[i]=='.'){
for(int k=0; k<26; ++k)
if(p->nt[k] && rec(p->nt[k],w,i+1))
return true;
}else if(p->nt[w[i]-'a'])
return rec(p->nt[w[i]-'a'],w,i+1);
return false;
}
};为了代码精简,也可以改成:
17.4 642. Design Search Autocomplete System
Design a search autocomplete system for a search engine. Users may input a sentence (at least one word and end with a special character ‘#’). For each character they type except ‘#’, you need to return the top 3 historical hot sentences that have prefix the same as the part of sentence already typed. Here are the specific rules:
The hot degree for a sentence is defined as the number of times a user typed the exactly same sentence before.
The returned top 3 hot sentences should be sorted by hot degree (The first is the hottest one). If several sentences have the same degree of hot, you need to use ASCII-code order (smaller one appears first).
If less than 3 hot sentences exist, then just return as many as you can.
When the input is a special character, it means the sentence ends, and in this case, you need to return an empty list.
Your job is to implement the following functions:
The constructor function:
AutocompleteSystem(String sentences, int times): This is the constructor. The input is historical data. Sentences is a string array consists of previously typed sentences. Times is the corresponding times a sentence has been typed. Your system should record these historical data.
Now, the user wants to input a new sentence. The following function will provide the next character the user types:
List
Example:
Operation: AutocompleteSystem([“i love you”, “island”,“ironman”, “i love leetcode”], [5,3,2,2])
The system have already tracked down the following sentences and their corresponding times:
“i love you” : 5 times
“island” : 3 times
“ironman” : 2 times
“i love leetcode” : 2 times
Now, the user begins another search:
Operation: input(‘i’)
Output: [“i love you”, “island”,“i love leetcode”]
Explanation:
There are four sentences that have prefix “i”. Among them, “ironman” and “i love leetcode” have same hot degree. Since ’ ’ has ASCII code 32 and ‘r’ has ASCII code 114, “i love leetcode” should be in front of “ironman”. Also we only need to output top 3 hot sentences, so “ironman” will be ignored.
Operation: input(’ ’)
Output: [“i love you”,“i love leetcode”]
Explanation:
There are only two sentences that have prefix “i”.
Operation: input(‘a’)
Output:
Explanation:
There are no sentences that have prefix “i a”.
Operation: input(‘#’)
Output:
Explanation:
The user finished the input, the sentence “i a” should be saved as a historical sentence in system. And the following input will be counted as a new search.
Note:
The input sentence will always start with a letter and end with ‘#’, and only one blank space will exist between two words.
The number of complete sentences that to be searched won’t exceed 100. The length of each sentence including those in the historical data won’t exceed 100.
Please use double-quote instead of single-quote when you write test cases even for a character input.
Please remember to RESET your class variables declared in class AutocompleteSystem, as static/class variables are persisted across multiple test cases. Please see here for more details.
https://leetcode.com/problems/design-search-autocomplete-system
17.4.1 Algo 1: Trie as unordered_map
class AutocompleteSystem {
unordered_map<string, int> m1; // s->freq
unordered_map<string, unordered_set<string>> m2;
string s;
public:
AutocompleteSystem(vector<string> ss, vector<int> ts) {
for(int i=0;i<ss.size();++i){
string t=ss[i];
m1[t]=ts[i];
for(int i=0;i<t.size();++i)
m2[t.substr(0,i+1)].insert(t);
}
}
vector<string> input(char c) {
if(c=='#'){
m1[s]++;
for(int i=0;i<s.size();++i)
m2[s.substr(0,i+1)].insert(s);
s="";
return {};
}
s+=c;
if(!m2.count(s)) return {};
vector<string> v;//str, freq
for(string e :m2[s])
v.emplace_back(e);
auto f=[&](string& s1, string& s2){
return m1[s1] > m1[s2] || (m1[s1] == m1[s2] && s1<s2);};
if(v.size()<3){
sort(v.begin(), v.end(), f);
return v;
}
nth_element(v.begin(), v.begin()+2, v.end(), f);
sort(v.begin(),v.begin()+3,f);
return vector<string>(v.begin(), v.begin()+3);
}
};This code gave Memory Limit Exceeded for a big test case. 这个算法的input的amortized复杂度是\(O(1)\).速度是非常快的,但是缺点就是太占空间,因为使用了trie的思想.
17.4.2 Algo 2: Priority Queue to Optimize Space
为了节约空间,我们可以考虑不使用trie,那么每次有新的input就loop现有的records寻找所有满足条件的records.
T: \(O(N*M)\) where N - length of historical records; M - Average length of records
class AutocompleteSystem { // 229 ms
unordered_map<string, int> dict;
string data;
public:
AutocompleteSystem(vector<string> sentences, vector<int> times) {
for (int i = 0; i < times.size(); i++)
dict[sentences[i]] += times[i];
data.clear();
}
vector<string> input(char c) {
if (c == '#') {
dict[data]++, data.clear();
return {};
}
data.push_back(c);
auto cmp = [](const pair<string, int> &a, const pair<string, int> &b) {
return a.second > b.second || a.second == b.second && a.first < b.first;
};
priority_queue<pair<string, int>, vector<pair<string, int>>, decltype(cmp)> pq(cmp);
for (auto &p : dict) { // O(N): N - length of historical records
bool match = true;
for (int i = 0; i < data.size(); i++) // O(M) M - Average length of records
if (data[i] != p.first[i]) { match = false; break; }
if (match) {
pq.push(p); // O(Log3)
if (pq.size() > 3) pq.pop(); // O(Log3)
}
}
vector<string> res(pq.size());
for (int i = pq.size() - 1; i >= 0; i--)
res[i] = pq.top().first, pq.pop();
return res;
}
};这个算法并不保存trie,而是实时的match,复杂度是O(N*(M+2Log3)),速度不快,但是节约了空间.因为trie实在是太耗空间了.
17.4.3 Algo 3: STL lower_bound and upper_bound
T: \(O(LogN + M*LogM)\)
struct AutocompleteSystem { // 193ms
AutocompleteSystem(const vector<string>& sentences, const vector<int>& times) {
for (int i = 0, n = sentences.size(); i < n; ++i)
m.emplace(sentences[i], times[i]);
}
vector<string> input(char c) { // O(LogN + M*LogM)
if (c == '#') {
++m[data], data.clear();
return vector<string>();
}
data.push_back(c);
auto b = m.lower_bound(data), e = m.upper_bound(data + "~"); // O(LogN)
map<int, set<string>, greater<int>> m2;
for (; b != e; ++b) // O(M)
m2[b->second].insert(b->first); // O(LogM)
vector<string> r;
for (auto& pr : m2)
for (auto& s : pr.second) {
r.push_back(s);
if (r.size() >= 3) return r;
}
return r;
}
string data;
map<string, int> m;
};这个算法充分利用了STL map(本质是红黑树)的特点.展示了如何在map里面做range query.比如historical records如下:
[...,he,hell,hellen,hello,helmet,henry,...,he~,...],然后用户输入了he,因为~是ASCII字母表里面最后一个可见字符,所以lower_bound("he")会返回指向’he’的iterator,upper_bound("he~")会返回指向’he~’之后的那个iterator,这样我们就找到一个range了.这题不适合用equal_range. lower_bound和upper_bound的使用是解这个题最最最关键的一点.而且你还需要知道~是ASCII表里面最后一个可见字符.
Fast Facts: ~ is the last visible char in ascii table.
找到了match的所有string之后,其余都很简单了,如何找到most frequent top 3是一个well known的问题.可以用priority_queue, nth_element,上面的代码使用了map,也没有太大的问题.
下面的代码试图使用nth_element达到线性复杂度,但是因为comparator调用了map的[]函数,所以复杂度反而更高.
T: \(O(M*LogN + 2M + 3Log3)\)
// 285ms
vector<string> input(char c) {
if (c == '#') {
++m[data], data.clear();
return vector<string>();
}
data.push_back(c);
auto b = m.lower_bound(data), e = m.upper_bound(data + "~"); // O(LogN)
vector<string> v;
auto f=[&](string& s1, string& s2){return m[s1] > m[s2] || (m[s1] == m[s2] && s1<s2);};
for (; b != e; ++b) /*O(M)*/ v.emplace_back(b->first); // O(1)
if(v.size()<=3){
sort(v.begin(), v.end(), f);
return v;
}
nth_element(v.begin(), v.begin()+2, v.end(), f); // O(M*LogN)
sort(v.begin(),v.begin()+3,f);
return vector<string>(v.begin(), v.begin()+3);
}17.5 648. Replace Words
In English, we have a concept called root, which can be followed by some other words to form another longer word - let’s call this word successor. For example, the root an, followed by other, which can form another word another.
Now, given a dictionary consisting of many roots and a sentence. You need to replace all the successor in the sentence with the root forming it. If a successor has many roots can form it, replace it with the root with the shortest length.
You need to output the sentence after the replacement.
Example 1:
Input: dict = ["cat", "bat", "rat"]
sentence = "the cattle was rattled by the battery"
Output: "the cat was rat by the bat"https://leetcode.com/problems/replace-words/
struct Solution {
string replaceWords(vector<string>& d, string s) {
istringstream is(s);
unordered_set<string> us(d.begin(), d.end());
string t, r, t2;
while(is >> t){
bool b=0;
for(int i=1;i<t.size() && !b;i++)
if(us.count(t2=t.substr(0,i))) r+=" "+t2, b=1;
if(!b) r+=" "+t;
}
return r.substr(1);
}
};需要用trie的地方大多使用这样的unordered_set,unordered_map来解决. 手写的trie结构太繁琐和占空间.
17.6 Suffix Tree
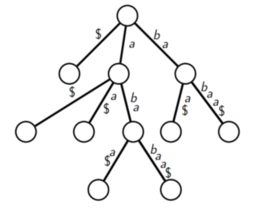
https://www.youtube.com/watch?v=amp1UcSKeCY
http://www.geeksforgeeks.org/ukkonens-suffix-tree-construction-part-1/
Problem: Number of unique subtring
#pragma once
#include <vector>
#include <string>
#include <set>
using namespace std;
bool startswith(string s, string h) {
return s.substr(0, h.size()) == h;
}
string second_part(string s, string h) {//
//return s.substr(h.size() - 1, s.size() - h.size());
return s.substr(h.size(), s.size() - h.size());
}
struct suffix_tree_node {
string s;// empty means root
set<suffix_tree_node*> c;
suffix_tree_node(string s_) :s(s_) {}
bool isleaf() { return c.empty(); }
};
using PSS = pair<suffix_tree_node*, string>;
PSS find_parent(suffix_tree_node* root, string suffix) {
for (suffix_tree_node* p : root->c) {
if (startswith(suffix, p->s)) {
string s2 = second_part(suffix, p->s); // na
return find_parent(p, s2);
}
}
return make_pair(root, suffix);
}
void insert(suffix_tree_node* root, string suffix) {
PSS p = find_parent(root, suffix);
p.first->c.insert(new suffix_tree_node(p.second));
}
suffix_tree_node* build_tree(const string& s) {
suffix_tree_node* root = new suffix_tree_node("");
for (int i = s.size() - 1; i >= 0; --i) {
string suffix = s.substr(i, s.size() - i);
insert(root, suffix);
}
return root;
}
int __helper(suffix_tree_node* r, int& sum) {
sum += r->s.size();
for (suffix_tree_node* p : r->c) {
__helper(p, sum);
}
return sum;
}
int unique_substring_num(suffix_tree_node* r) {
int s = 0;
return __helper(r, s);
}
int main(int argc, char** argv) {
suffix_tree_node* r = build_tree("banana");
int su = unique_substring_num(r);
cout << su << endl;
}Longest Palindromic Substring
http://www.geeksforgeeks.org/suffix-tree-application-6-longest-palindromic-substring/