Chapter 16 Tree Traversal
Note: Traversal(\(O(N)\)) is different from search(\(O(LogN)\)).
In/Pre/Post-Order Traversal are all of DFS algorithm.
16.1 Morris Traversal
Morris只提供了中序遍历的方法,在中序遍历的基础上稍加修改可以实现前序,而后续就要再费点心思了.这篇文章把三种方法都列出来了: http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html
16.1.1 Morris Traversal InOrder (Two pointers)
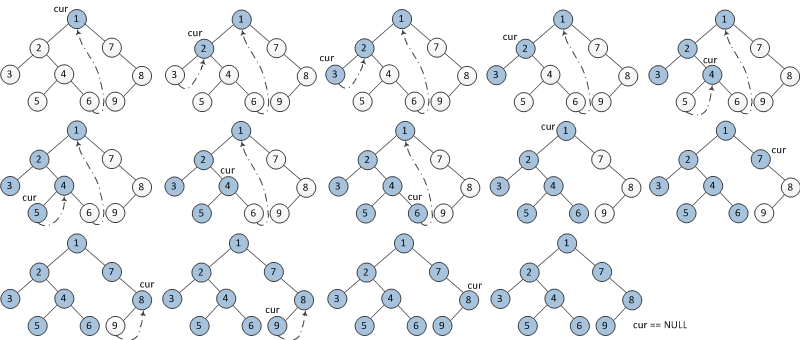
The Morris is the M in KMP algo.
Version 1: Tree is modified.
int kthSmallest(TreeNode* c, int k) {
if (!c || k <= 0) return 0;
TreeNode *p=NULL;
while (c) {
if (c->left) {
p = c->left;
while (p->right) p = p->right;
TreeNode *t=c; c=c->left, t->left=NULL, p->right=t;
} else {
if (k == 1) return c->val;
k--, c = c->right; //when c->left==NULL, visit!!!
}
}
return 0;
}这个函数的结果把所有的节点用right node关系从大到小链接起来了!!!其实就是等同于下面这个面试题:
- flatten bst成为linkedlist,要求最后的linkedlist必须是sorted而且不能占用额外的空间.
Version 2: Tree is restored.
在恢复树的时候visit节点.
// Morris Traversal - Tree is modified and restored!!! - O(N)
vector<int> inorderTraversal(TreeNode* c) {
vector<int> r;
if (!c)return r;
TreeNode *p = NULL;
while (c) {
if (c->left){
p = c->left;
while (p->right && p->right != c) p = p->right;
if (p->right) { // unwind stack
r.push_back(c->val);// visit!
p->right = 0, c = c->right;// 恢复树
} else
p->right = c, c = c->left; // connect to successor后继
}else
r.push_back(c->val), c = c->right;// visit!让c向p靠近
}
return r;
}Version 2’s while condition is more complex, when backtrackig, c is set to c->right, else c is set to c->left to move forward.
https://en.wikipedia.org/wiki/Threaded_binary_tree#The_array_of_Inorder_traversal
http://blog.csdn.net/zone_programming/article/details/50573840
http://www.cnblogs.com/AnnieKim/archive/2013/06/15/MorrisTraversal.html
16.2 94. Binary Tree Inorder Traversal
Given a binary tree, return the inorder traversal of its nodes’ values.
For example: Given binary tree [1,null,2,3],
1
\
2
/
3return [1,3,2]
Note: Recursive solution is trivial, could you do it iteratively?
https://leetcode.com/problems/binary-tree-inorder-traversal/
很详细的解释: http://bit.ly/2vMxedv
16.2.2 Algo 1: Iterative Traversal with Linear Space O(N)
模板是7 Line Iterative Inorder Traversal Code withstack:
void inorderTraversal(TreeNode* c) {
stack<TreeNode> stk;
while (c or !stk.empty()) {
while(c) stk.push(c), c = c->left;// push all leftish nodes into stack c = stk.top(), stk.pop(), /visit(c)*/ c = c->right;// peek at top of stack } // at this point, c==0 and stack is empty, which means our work is done }
上题的iterative解法的代码如下:
16.2.3 Algo 2: Morris Traversal with Constant Space O(1)
struct Solution { // lRr
vector<int> inorderTraversal(TreeNode* c) {
vector<int> r;
while (c) {
if (c->left){
auto p = c->left;
while (p->right && p->right != c) p = p->right;
if (p->right) { // unwind stack
r.push_back(c->val);// visit!
p->right = 0, c = c->right;// 恢复树
} else
p->right = c, c = c->left; // connect to successor后继
}else
r.push_back(c->val), c = c->right;// visit!让c向p靠近
}
return r;
}
};16.3 783. Minimum Distance Between BST Nodes
Given a Binary Search Tree (BST) with the root node root, return the minimum difference between the values of any two different nodes in the tree.
Example :
Input: root = [4,2,6,1,3,null,null]
Output: 1
Explanation:
Note that root is a TreeNode object, not an array.The given tree [4,2,6,1,3,null,null] is represented by the following diagram:
4
/ \
2 6
/ \
1 3 while the minimum difference in this tree is 1, it occurs between node 1 and node 2, also between node 3 and node 2.
https://leetcode.com/problems/minimum-distance-between-bst-nodes/
16.4 98. Validate Binary Search Tree
https://leetcode.com/problems/validate-binary-search-tree
16.4.2 Algo 2: Regular Iterative Traversal with stack
struct Solution {
bool isValidBST(TreeNode* c) {
stack<TreeNode*> stk;
long long tmp=INT_MIN-1L; // L is important
while(!stk.empty() || c){
while(c) stk.push(c), c=c->left;
if(tmp!=INT_MIN-1L && tmp>=stk.top()->val)
return false;
tmp=stk.top()->val, c=stk.top()->right, stk.pop();
}
return true;
}
};16.4.3 Algo 3: Morris Iterative Traversal
Check tree-traversal for Morris Traversal.
struct Solution {
bool isValidBST(TreeNode* c) {
long long prev=INT_MIN-1L;
while(c){
if(c->left){
TreeNode* p=c->left;
while(p->right) p=p->right;
p->right=c;
TreeNode* tmp=c;
c=c->left, tmp->left=0;
}else{
if (prev!=INT_MIN-1L && prev>=c->val)
return false;
prev=c->val;
c=c->right;
}
}
return 1;
}
};16.5 230. Kth Smallest Element in a BST
https://leetcode.com/problems/kth-smallest-element-in-a-bst/
struct Solution {
int nn(TreeNode* root){ // node number
if (not root) return 0;
return nn(root->left) + nn(root->right) + 1;
}
int kthSmallest_2(TreeNode* root, int k) {
int l = nn(root->left);
int r = nn(root->right);
if (l+1==k) return root->val;
else if(l+1<k){
return kthSmallest(root->right,k-l-1);
}else{
return kthSmallest(root->left,k);
}
}
int kthSmallest(TreeNode* c, int k) {
if(!c || k<=0) return 0;
TreeNode *p, *t;
while(c){
if(c->left){
t = p = c->left;
while(p->right) p = p->right;
c->left=0, p->right=c, c=t;
}else{
if(k == 1) return c->val;
k--, c = c->right;
}
}
return 0;
}
};16.6 285. Inorder Successor in BST
Given a binary search tree and a node in it, find the in-order successor of that node in the BST.
Note: If the given node has no in-order successor in the tree, return null.
https://leetcode.com/problems/inorder-successor-in-bst/
CLRS P292
http://www.geeksforgeeks.org/inorder-successor-in-binary-search-tree/
http://www.cnblogs.com/grandyang/p/5306162.html
找继承.CLRS上面的例子就是有父节点的情况.但是这道题是没有父节点.
有父节点:
Case 1:
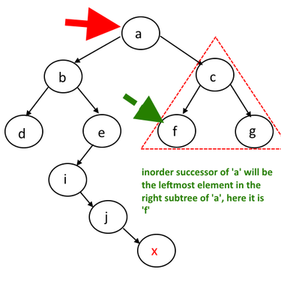
Case 2:
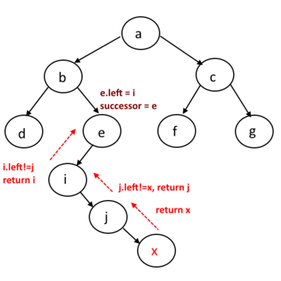
struct node * inOrderSuccessor(struct node *root, struct node *n){
if( n->right ) return minValue(n->right); // 1. 有右子树就往下走
struct node *p = n->parent; // step 2 of the above algorithm
while(p && n == p->right) // 2. 无右子树就沿着父节点往上走
n = p,p = p->parent;
return p;
}无父节点:
struct Solution {
TreeNode* inorderSuccessor(TreeNode* R, TreeNode* p) {
TreeNode* suc=0;
while(R){
if(p->val < R->val){
suc=R, R=R->left;
}else R=R->right;
}
return suc;
}
};这个是我看到最简洁的写法:
struct Solution {
TreeNode* inorderSuccessor(TreeNode* R, TreeNode* p) { // O(H)
TreeNode* suc=0;
while(R) R = (R->val > p->val) ? (suc=R)->left : R->right;
return suc;
}};
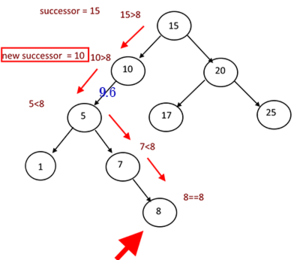
上面写法虽然简洁,却不是最高效的.虽然复杂度都是\(O(H)\),下面这个应该高效一些:
16.7 270. Closest Binary Search Tree Value
https://leetcode.com/problems/closest-binary-search-tree-value
class Solution {
public:
int closestValue(TreeNode* root, double target) {
long long pre=INT_MAX, suc=INT_MAX;
while (root)
if (target < root->val)
suc=root->val, root=root->left;
else
pre=root->val, root=root->right;
if(suc==INT_MAX) return pre;
if(pre==INT_MAX) return suc;
return (suc-target)>(target-pre)?pre:suc;
}
};16.8 272. Closest Binary Search Tree Value II
Given a non-empty binary search tree and a target value, find k values in the BST that are closest to the target.
Note:
Given target value is a floating point.
You may assume k is always valid, that is: k ≤ total nodes.
You are guaranteed to have only one unique set of k values in the BST that are closest to the target.
Follow up:
Assume that the BST is balanced, could you solve it in less than \(O(n)\) runtime (where n = total nodes)?
Hint:
Consider implement these two helper functions:
getPredecessor(N), which returns the next smaller node to N.
getSuccessor(N), which returns the next larger node to N.
https://leetcode.com/problems/closest-binary-search-tree-value-ii/
http://www.cnblogs.com/grandyang/p/5247398.html
struct Solution {
vector<int> closestKValues(TreeNode* R, double T, int k) {
vector<int> r;
stack<TreeNode*> pre, suc;
while (R)
if (R->val <= T) pre.push(R), R = R->right; else suc.push(R), R = R->left;
while (k--)
if (suc.empty() || !pre.empty() && T - pre.top()->val < suc.top()->val - T)
r.push_back(pre.top()->val), push_pre(pre);
else
r.push_back(suc.top()->val), push_suc(suc);
return r;
}
void push_pre(stack<TreeNode*>& stk) {
TreeNode *t = stk.top(); stk.pop();
if (!t->left) return;
stk.push(t->left);
while (stk.top()->right) stk.push(stk.top()->right);
}
void push_suc(stack<TreeNode*>& stk) {
TreeNode *t = stk.top(); stk.pop();
if (!t->right) return;
stk.push(t->right);
while (stk.top()->left) stk.push(stk.top()->left);
}
};
true || blah …. blah 如果第一个是true ||, 会把后面所有的短路掉,不管有多少||或者&&.
16.9 144. Binary Tree Preorder Traversal
https://leetcode.com/problems/binary-tree-preorder-traversal/
16.10 255. Verify Preorder Sequence in Binary Search Tree
https://leetcode.com/problems/verify-preorder-sequence-in-binary-search-tree/
16.11 145. Binary Tree Postorder Traversal
https://leetcode.com/problems/binary-tree-postorder-traversal/
16.12 99. Recover Binary Search Tree
16.13 113. Path Sum II
16.14 173. Binary Search Tree Iterator
https://leetcode.com/problems/binary-search-tree-iterator/
https://discuss.leetcode.com/topic/57838/4ms-java-solution-beats-99-83/5
/**Your BSTIterator will be called like this:
* BSTIterator i = BSTIterator(root);
* while (i.hasNext()) cout << i.next(); */
class BSTIterator {
TreeNode *c;
BSTIterator(TreeNode *root) { c = root; }
bool hasNext() { return c!=NULL; }
int next() {
TreeNode* p;
while(c){
if(c->left){
p = c->left;
#if RESTORE_TREE
while(p->right && p->right!=c) p = p->right;
if(p->right){
p->right=0;
break; //c = c->right;
}else
p->right=c, c=c->left;
#ELSE
TreeNode* t = p;
while(p->right) p = p->right;
c->left=0, p->right=c, c = t;
#ENDIF
}else{
break; //c = c->right;
}
}
int r = c->val;
c = c->right;
return r;
}
};Other solutions: iterator
Other Method[not verified yet]:
http://math-porn.tumblr.com/post/98314044394/the-ouroboros-algorithm-a-constant-space-tree
16.15 Tree Search
Tree search uses Recursion.
T: O(LogN)
Don’t use Traversal to do search problem!
- Closest Binary Search Tree Value
https://leetcode.com/problems/closest-binary-search-tree-value/
16.16 545. Boundary of Binary Tree
https://leetcode.com/problems/boundary-of-binary-tree
http://www.geeksforgeeks.org/boundary-traversal-of-binary-tree/
Given a binary tree, return the values of its boundary in anti-clockwise direction starting from root. Boundary includes left boundary, leaves, and right boundary in order without duplicate nodes.
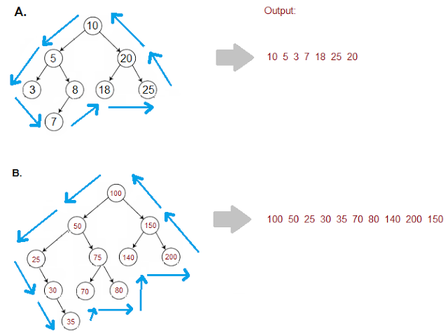
Algo:
1. Print Left boundary Nodes.
2. Print Leaf Nodes.
3. Print Right boundary Nodes in Bottom up fashion.
struct Solution {
vector<int> boundaryOfBinaryTree(TreeNode* root) {
vector<int> r;
if(root){
r.push_back(root->val);
left(r,root->left);
leaf(r,root->left), leaf(r,root->right);
right(r,root->right);
}
return r;
}
void left(vector<int>& r, TreeNode* n){
if(!n) return;
if(n->left){ r.push_back(n->val), left(r,n->left); }
else if(n->right){ r.push_back(n->val), left(r,n->right); }
//else r.push_back(n->val);
}
void leaf(vector<int>& r, TreeNode* n){
if(!n) return;
leaf(r,n->left);
if(!n->left && !n->right){ r.push_back(n->val); return;}
leaf(r,n->right);
}
void right(vector<int>& r, TreeNode* n){
if(!n) return;
if(n->right){ right(r,n->right), r.push_back(n->val); }
else if(n->left){ right(r,n->left), r.push_back(n->val); }
//else r.push_back(n->val);// last leaf
}
};16.17 538. Convert BST to Greater Tree
https://leetcode.com/problems/convert-bst-to-greater-tree
Input: The root of a Binary Search Tree like this:
5
/ \
2 13
Output: The root of a Greater Tree like this:
18
/ \
20 13这道题只要从大往小遍历BST就可以了,也就是DFS先右后左,记录已经遍历过的节点的值的和,每遍历到一个新节点就把节点值加上这个和.It is Reverse-Inorder Traversal.
16.18 536. Construct Binary Tree from String
https://leetcode.com/problems/construct-binary-tree-from-string/#/description
Input: "4(2(3)(1))(6(5))"
Output: return the tree root node representing the following tree:
4
/ \
2 6
/ \ /
3 1 5 对于例题中的“4(2(3)(1))(6(5))”,可知4是根节点,“2(3)(1)”是左子树,“6(5)”是右子树.可以想到应该用递归的方式建树. 这里怎么判断它的左子树的开始和结尾呢? 通过对“()”进行计数,当遇到’(‘加1,遇到’)’减去1.当为0时,说明括号是完全匹配的,此时它自己可以形成一个新树.剩下的就是加括号的右子树的字符串.
class Solution {
public:
TreeNode* str2tree(string s) {
int i = 0;
return s.size() == 0 ? nullptr : build(s, i);
}
private:
TreeNode* build(string& s, int& i) {
int start = i;
if (s[i] == '-') i++;
while (isdigit(s[i])) i++;
int num = stoi(s.substr(start, i - start));
TreeNode* node = new TreeNode(num);
if (s[i] == '(') { node->left = build(s, ++i); i++;/*)*/ }
if (s[i] == '(') { node->right = build(s, ++i);i++;/*)*/ }
return node;
}
};DFS遍历的Parenthesis structure. CLRS P606.
16.19 508. Most Frequent Subtree Sum
https://leetcode.com/problems/most-frequent-subtree-sum
Given the root of a tree, you are asked to find the most frequent subtree sum. The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself). So what is the most frequent subtree sum value? If there is a tie, return all the values with the highest frequency in any order.
Examples 1
Input:
5
/ \
2 -3return [2, -3, 4], since all the values happen only once, return all of them in any order.
Examples 2
Input:
5
/ \
2 -5return [2], since 2 happens twice, however -5 only occur once.
Note: You may assume the sum of values in any subtree is in the range of 32-bit signed integer.
class Solution {
public:
vector<int> findFrequentTreeSum(TreeNode* root) {
unordered_map<int, int> C; // counter
int mx=0;
rec(root, C, mx);
vector<int> r;
for_each(C.begin(), C.end(),
[&](const pair<int,int>& p){if(p.second==mx) r.push_back(p.first);});
return r;
}
int rec(TreeNode* n, unordered_map<int, int>& C, int& mx){
if(!n) return 0;
int sm1=rec(n->left,C,mx);
int sm2=rec(n->right,C,mx);
int sum = n->val + sm1 + sm2;
++C[sum], mx=max(mx,C[sum]);
return sum;
}
};16.20 Convert a Binary Tree to Threaded binary tree
http://www.geeksforgeeks.org/convert-binary-tree-threaded-binary-tree-set-2-efficient/
Idea of Threaded Binary Tree is to make inorder traversal faster and do it without stack and without recursion. In a simple threaded binary tree, the NULL right pointers are used to store inorder successor. Where-ever a right pointer is NULL, it is used to store inorder successor.
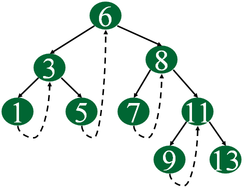
上图中1,5,7,9叫做threaded node.
16.21 257. Binary Tree Paths
https://leetcode.com/problems/binary-tree-paths
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> r;
dfs(r,"",root);
return r;
}
void dfs(vector<string>& r, string p, TreeNode* n){
if(!n) return;
if(!n->left && !n->right){
p+="->"+to_string(n->val);
r.push_back(p.substr(2,p.size()-2));
return;
}
p+="->"+to_string(n->val);
dfs(r,p,n->left);
dfs(r,p,n->right);
}
};在这个例子中,partial solution p用pass by value比较好, 这样不用pop_back().
16.22 314. Binary Tree Vertical Order Traversal
Given a binary tree, return the vertical order traversal of its nodes’ values. (ie, from top to bottom, column by column).
If two nodes are in the same row and column, the order should be from left to right.
Examples:
Given binary tree [3,9,20,null,null,15,7],
3
/\
/ \
9 20
/\
/ \
15 7return its vertical order traversal as: [ [9], [3,15], [20], [7] ]
Given binary tree [3,9,8,4,0,1,7],
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7return its vertical order traversal as: [ [4], [9], [3,0,1], [8], [7] ]
Given binary tree [3,9,8,4,0,1,7,null,null,null,2,5] (0’s right child is 2 and 1’s left child is 5),
3
/\
/ \
9 8
/\ /\
/ \/ \
4 01 7
/\
/ \
5 2return its vertical order traversal as: [ [4], [9,5], [3,0,1], [8,2], [7] ]
https://leetcode.com/problems/binary-tree-vertical-order-traversal
解题的第一步是求出左右两边相对于root的长度,DFS和BFS都可以搞定其实; 第二步是通过index把数值填到相应的坑里面.
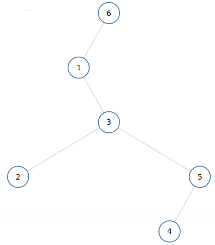
一上来没看清楚题意,用了two DFS的解法.
struct Solution {
vector<vector<int>> verticalOrder(TreeNode* root) {
if(!root) return vector<vector<int>>();
int ml=0, mr=0;
dfs1(root,0,0,ml,mr);
int L=ml+mr+1;
vector<vector<int>> rt(L, vector<int>());
dfs2(rt, root, ml);
return rt;
}
void dfs1(TreeNode* n, int l, int r, int& ml, int& mr){
if(!n) return;
dfs1(n->left,l+1,r,ml,mr);
dfs1(n->right,l,r+1,ml,mr);
ml = max(ml, l-r);
mr = max(mr, r-l);
}
void dfs2(vector<vector<int>>& r, TreeNode* n, int idx){
if(!n) return;
r[idx].push_back(n->val);
dfs2(r,n->left,idx-1);
dfs2(r,n->right,idx+1);
}
};结果得到一个error:
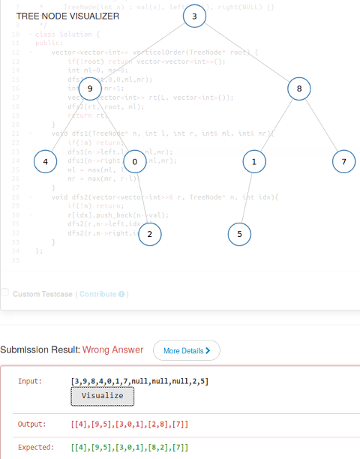
才发现题目要求结果中的node要from top to bottom. 转念一想,BFS也是没有问题的. 代码如下:
struct Solution {
vector<vector<int>> verticalOrder(TreeNode* root) {
if(!root) return vector<vector<int>>();
int ml=0, mr=0;
dfs(root,0,0,ml,mr);
int L=ml+mr+1;
vector<vector<int>> rt(L, vector<int>());
bfs(rt, root, ml);
return rt;
}
void dfs(TreeNode* n, int l, int r, int& ml, int& mr){
if(!n) return;
dfs(n->left,l+1,r,ml,mr);
dfs(n->right,l,r+1,ml,mr);
ml = max(ml, l-r), mr = max(mr, r-l);
}
void bfs(vector<vector<int>>& r, TreeNode* n, int idx){
queue<pair<TreeNode*, int>> q;
q.push({n,idx});
while(!q.empty()){
int sz=q.size();
while(sz--){
auto t=q.front(); q.pop();
r[t.second].push_back(t.first->val);
if(t.first->left) q.push({t.first->left, t.second-1});
if(t.first->right) q.push({t.first->right, t.second+1});
}
}
}
};这里第一步得到ml和mr所用的DFS用BFS也可以得到. 如果把题目要求改为from left to right,就是上面的“错误”的那个算法.
16.23 652. Find Duplicate Subtrees
Given a binary tree, return all duplicate subtrees. For each kind of duplicate subtrees, you only need to return the root node of any one of them.
Two trees are duplicate if they have the same structure with same node values.
Example 1:
1
/ \
2 3
/ / \
4 2 5
/ /
5 4
/
5The following are three duplicate subtrees:
2
/
4
/
5and
4
/
5and
5Therefore, you need to return above trees’ root in the form of a list/vector.
https://leetcode.com/problems/find-duplicate-subtrees
上面提到有3颗duplicate trees:[2,4,5],[4,5]和[5], [2,4,5]和[4,5]有两个duplicates,但是[5]有3个duplicates. 要求我们返回节点[2,4,5]
subtree的问题一般两个办法,一个是用is_same_tree来检测, 一个是用preorder string,通常后一个效果比较好. 这道题前一个方法我做了超时了.用后一个方法就极其简单.
Use preorder with delimiter represents a unique binary tree. 用DFS traversal, 当我们走到一个node的时候,要它的preorder string,然后放到map里面看是否曾经有过这样的preorder string,如果刚好有一个就加入final result; 而且不管有没有都increase counter by 1, 以防止重复加入.
struct Solution {
unordered_map<string, int> m;
vector<TreeNode*> r;
vector<TreeNode*> findDuplicateSubtrees(TreeNode* R) {
dfs(R);
return r;
}
string dfs(TreeNode* n){
if (!n) return "x";
string s = dfs(n->left) + ","+to_string(n->val) +"," + dfs(n->right)+"-"; // inorder
//string s = dfs(n->right) + ","+to_string(n->val) +"," + dfs(n->left)+"-"; // reverse-inorder
//string s = to_string(n->val) +"," + dfs(n->left) + ","+ dfs(n->right); // preorder
//string s = dfs(n->right) + ","+ dfs(n->left) + "," + to_string(n->val); // reverse-preorder
//string s = dfs(n->left) + ","+ dfs(n->right) + "," + to_string(n->val); // postorder
//string s = to_string(n->val)+ ","+dfs(n->right) + ","+ dfs(n->left); // reverse-postorder
//cout << s << endl;
if (m[s]++ == 1) r.push_back(n);
return s;
}
};这道题的string用preorder, postorder都可以,但是inorder要注意一下,对每层stackframe计算完之后要加一个标记.和subtree-of-another-tree的第二个解法类似.
我在用g++调试时发现第10行子表达式的计算顺序是从右到左,这在C++标准里面是没有规定的. 同样道理的有函数参数的入栈顺序.
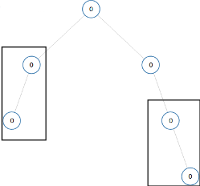
如果用inorder traversal with delimiter,上图的两个边框里面的subtree都是“x,0,x,0,x”,所以必须在尾部加一个标记.
这个性质其实在Serialize and Deserialize Binary Tree里面已经使用过了.