Chapter 15 Binary Tree (Continued)
15.1 96. Unique Binary Search Trees
https://leetcode.com/problems/unique-binary-search-trees/
//TODO
15.2 95. Unique Binary Search Trees II
https://leetcode.com/problems/unique-binary-search-trees-ii/
//TODO
15.3 241. Different Ways to Add Parentheses
https://leetcode.com/problems/different-ways-to-add-parentheses/
public class Solution {
Map<String, List<Integer>> map = new HashMap<>();
public List<Integer> diffWaysToCompute(String input) {
if (map.containsKey(input)) return map.get(input);
List<Integer> res = new ArrayList<>();
if (input == null || input.length() == 0) return res;
for (int i = 0; i < input.length(); i++) {
char c = input.charAt(i);
if (c == '+' || c == '-' || c == '*') {
List<Integer> leftNums = diffWaysToCompute(input.substring(0, i));
List<Integer> rightNums = diffWaysToCompute(input.substring(i + 1));
for (int left : leftNums) {
for (int right : rightNums) {
if (c == '+') res.add(left + right);
else if (c == '-') res.add(left - right);
else if (c == '*') res.add(left * right);
}
}
}
}
if (res.size() == 0) res.add(Integer.parseInt(input));
map.put(input, res);
return res;
}
}15.4 449. Serialize and Deserialize BST
https://leetcode.com/problems/serialize-and-deserialize-bst/
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary search tree can be serialized to a string and this string can be deserialized to the original tree structure.
The encoded string should be as compact as possible.
Note: Do not use class member/global/static variables to store states. Your serialize and deserialize algorithms should be stateless.
因为通过pre/post order就可以唯一的确定一颗BST,和上一题相比,我们可以省去null marker.其实就是pre/post order traversal然后re-construct.
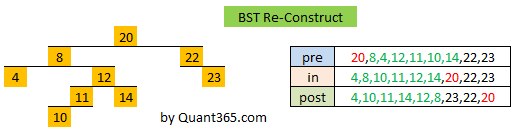
http://stackoverflow.com/questions/12880718/how-many-traversals-need-to-be-known-to-construct-a-bst
struct Codec {
string serialize(TreeNode* root) { // preorder
if (!root) return "";
//return to_string(root->val) + "," + serialize(root->left)+","+serialize(root->right);
string R=to_string(root->val);
string l=serialize(root->left), r=serialize(root->right);
if(!l.empty()) R+=","+l;
if(!r.empty()) R+=","+r;
return R;
}
TreeNode* deserialize(string data) {
vector<int> v;
istringstream is(data);
string t;
while(getline(is, t, ',')) v.push_back(stoi(t));
return rec(v, 0, v.size()-1);
}
TreeNode* rec(vector<int>& v, int h, int t){
if(h>t) return 0; //!!
TreeNode* R=new TreeNode(v[h]);
int i=h+1;
for(;i<=t;++i) if(v[h]<v[i]) break;// like the STL find in previous problem
R->left = rec(v,h+1,i-1);
R->right = rec(v,i,t);
return R;
}
};注意和前面的相比,serialize代码还比较麻烦,因为不需要对null和叶子节点做任何标记,所以要去除不必要的分隔符, in this case.
This is a iterative version written by Python:
class Codec:
def serialize(self, root):
if not root: return ''
left = self.serialize(root.left)
right = self.serialize(root.right)
ans = str(root.val)
if left: ans += ',' + left
if right: ans += ',' + right
return ans
def deserialize(self, data):
if not data: return None
nstack, rstack = [], [0x7FFFFFFF]
for val in map(int, data.split(',')):
node = TreeNode(val)
if nstack:
if val < nstack[-1].val:
nstack[-1].left = node
rstack.append(nstack[-1].val)
else:
while val > rstack[-1]:
while nstack[-1].val > nstack[-2].val:
nstack.pop()
rstack.pop()
nstack.pop()
nstack[-1].right = node
nstack.append(node)
return nstack[0]15.5 129. Sum Root to Leaf Numbers
Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.
An example is the root-to-leaf path 1->2->3 which represents the number 123.
Find the total sum of all root-to-leaf numbers.
For example,
1
/ \
2 3The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Return the sum = 12 + 13 = 25.
https://leetcode.com/problems/sum-root-to-leaf-numbers/
一看这个题需要用recursive来解.同一个root在不同深度的路上值是不相同的,在递归之前,你不知道它的值或者深度是多少.这个题和求深度那个题很像.
struct Solution {
int sumNumbers(TreeNode* root) {return rec(root, 0);}
int rec(TreeNode* root, int p){
if(root==0) return 0;
if(root->left==0 && root->right==0) return p*10+root->val;//!!
return rec(root->left, root->val+p*10) + rec(root->right, root->val+p*10);
}
};递归函数的设计:
1. 返回值是否为void还是其他值
2. 是否传reference还是传值
二叉树并不是所有的点都相同,leaf和inner点不同.有三种类型的点:
1. leaf node
2. NULL node
3. inner with one or two children node
写和验证算法的时候想想如何满足这三类点.如果都满足就OK.
15.6 199. Binary Tree Right Side View
https://leetcode.com/problems/binary-tree-right-side-view/
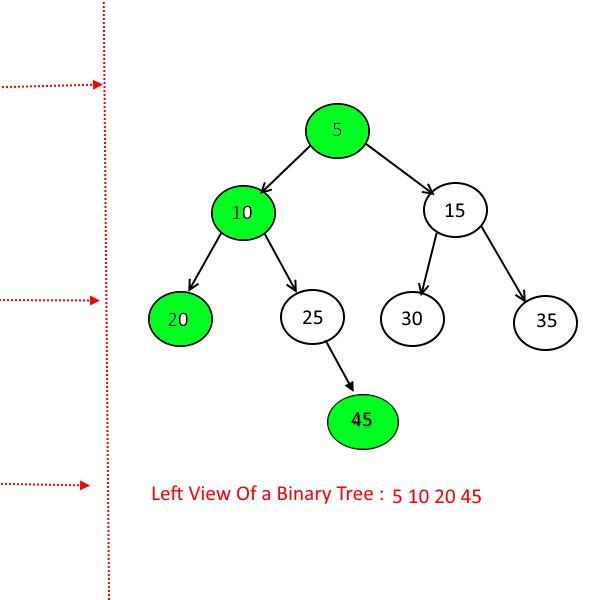
For illustration purpose only, 下面这个图是left view, 我们要求的是right view.
struct Solution {
vector<int> rightSideView(TreeNode* root) {
vector<int> r;
int maxdepth=0;
dfs(r,root,maxdepth,0);
return r;
}
void dfs(vector<int>& r, TreeNode* n, int& maxdepth, int curdepth){
if(n==NULL) return;
curdepth++;
if(maxdepth<curdepth){maxdepth=curdepth; r.push_back(n->val);}
dfs(r,n->right,maxdepth,curdepth);
dfs(r,n->left, maxdepth,curdepth);
}
};这题用BFS可以做,但其实DFS给出最优美的解答. 这题主要考察在DFS中全局变量和局部变量的处理. maxdepth就是全局的,采用传引用(其实传指针也行),在traversal的时候是有变化的,而且这个变化是永久的,在stack unwind之后值也是变化了的. curdepth就是当前层的depth,是一个局部的变量,采用传参数,在stack unwind之后仍然是在该层的值,与前后stack frame的任何变化都没有关系.
15.7 623. Add One Row to Tree
Given the root of a binary tree, then value v and depth d, you need to add a row of nodes with value v at the given depth d. The root node is at depth 1.
The adding rule is: given a positive integer depth d, for each NOT null tree nodes N in depth d-1, create two tree nodes with value v as N’s left subtree root and right subtree root. And N’s original left subtree should be the left subtree of the new left subtree root, its original right subtree should be the right subtree of the new right subtree root. If depth d is 1 that means there is no depth d-1 at all, then create a tree node with value v as the new root of the whole original tree, and the original tree is the new root’s left subtree.
Example 1:
Input:
A binary tree as following:
4
/ \
2 6
/ \ /
3 1 5
v = 1
d = 2
Output:
4
/ \
1 1
/ \
2 6
/ \ /
3 1 5 Example 2:
Input:
A binary tree as following:
4
/
2
/ \
3 1
v = 1
d = 3
Output:
4
/
2
/ \
1 1
/ \
3 1https://leetcode.com/problems/add-one-row-to-tree
算法用BFS,下面的解法比OJ上面要求还要多些. 如果输入的深度d大于树的深度+1,就自动append到最底层.下面的代码展示如何得到最底层.
struct Solution {
TreeNode* addOneRow(TreeNode* root, int v, int d) {
if(d==1){
TreeNode* R=new TreeNode(v);
R->left=root;
return R;
}
queue<TreeNode*> q, q2; // q2 is the last layer
q.push(root);
int ly=0, inserted=0;
while(!q.empty()){
ly++;
int sz=q.size();
q2 = q;
while(sz--){
auto t=q.front();
if(d==ly+1){ // insertion happens here...
inserted = 1;
auto l = t->left, r = t->right; // store as temp
t->left=new TreeNode(v);
t->left->left=l;
t->right=new TreeNode(v);
t->right->right=r;
}else{
if(t->left ){ q.push(t->left); }
if(t->right){ q.push(t->right);}
}
q.pop();
}
if(d==ly+1) break;
}
if(inserted==0){
while(!q2.empty()){
auto t=q2.front();
t->left=new TreeNode(v), t->right=new TreeNode(v);
q2.pop();
}
}
return root;
}
};15.8 572. Subtree of Another Tree
Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.
Example 1:
Given tree s:
3
/ \
4 5
/ \
1 2Given tree t:
4
/ \
1 2Return true, because t has the same structure and node values with a subtree of s.
Example 2:
Given tree s:
3
/ \
4 5
/ \
1 2
/
0Given tree t:
4
/ \
1 2Return false.
https://leetcode.com/problems/subtree-of-another-tree/
15.8.1 Algo 1: Recusion
This is just a tree version of strstr().
struct Solution {
bool isSubtree(TreeNode* s, TreeNode* t) {
if(t==0) return 1; else if(s==0) return 0;
if((s && t) && (s->val==t->val) && is_same(s,t)) return true;
return isSubtree(s->left, t) || isSubtree(s->right, t);
}
bool is_same(TreeNode* s, TreeNode* t){
if(s==t) return 1;
if((s&&t)==0 || s->val!=t->val) return 0;
return is_same(s->left, t->left) && is_same(s->right, t->right);
}
};15.8.2 Algo 2: Serialize Binary Tree
下面的解法用到了之前那道Serialize and Deserialize Binary Tree的解法,思路是对s和t两棵树分别进行序列化,各生成一个字符串,如果t的字符串是s的子串的话,就说明t是s的子树,但是需要注意的是,为了避免出现[12], [2], 这种情况,虽然2也是12的子串,但是[2]却不是[12]的子树,所以我们再序列化的时候要特殊处理一下,就是在每个结点值前面都加上一个字符,比如’s’,来分隔开,那么[12]序列化后就是“,12,x”,而[2]序列化之后就是“,2,x”,这样就可以完美的解决之前的问题了,参见代码如下:
struct Solution {
bool isSubtree(TreeNode* s, TreeNode* t) {
string s1=dfs(s), s2=dfs(t);
return s1.find(s2) != string::npos;
}
string dfs(TreeNode* n){
if(!n){ return "x";}
return "s"+to_string(n->val)+","+dfs(n->left)+","+dfs(n->right);
}
};这道题pre/post/inorder都可以解题! 这里用的仅是preorder.
这个题的follow-up是Find Duplicate Subtrees.
15.9 404. Sum of Left Leaves
Find the sum of all left leaves in a given binary tree.
Example:
3
/ \
9 20
/ \
15 7There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
15.10 298. Binary Tree Longest Consecutive Sequence
Given a binary tree, find the length of the longest consecutive sequence path.
The path refers to any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The longest consecutive path need to be from parent to child (cannot be the reverse).
For example,
1
\
3
/ \
2 4
\
5Longest consecutive sequence path is 3-4-5, so return 3.
2
\
3
/
2
/
1Longest consecutive sequence path is 2-3, not 3-2-1, so return 2.
https://leetcode.com/problems/binary-tree-longest-consecutive-sequence
class Solution {
int mx=1;
public:
int longestConsecutive(TreeNode* root) {
if(!root) return 0;
dfs(root->left, root->val, 1);
dfs(root->right, root->val, 1);
return mx;
}
void dfs(TreeNode* t, int parent, int c){
if(!t) return;
if(t->val==parent+1) c++; else c=1;
mx=max(mx, c);
dfs(t->left, t->val, c);
dfs(t->right, t->val, c);
}
};15.11 655. Print Binary Tree
Print a binary tree in an m*n 2D string array following these rules:
The row number m should be equal to the height of the given binary tree.
The column number n should always be an odd number.
The root node’s value (in string format) should be put in the exactly middle of the first row it can be put. The column and the row where the root node belongs will separate the rest space into two parts (left-bottom part and right-bottom part). You should print the left subtree in the left-bottom part and print the right subtree in the right-bottom part. The left-bottom part and the right-bottom part should have the same size. Even if one subtree is none while the other is not, you don’t need to print anything for the none subtree but still need to leave the space as large as that for the other subtree. However, if two subtrees are none, then you don’t need to leave space for both of them.
Each unused space should contain an empty string "".
Print the subtrees following the same rules.
Example 1:
Input:
1
/ \
2 5
/
3
/
4
Output:
[["", "", "", "", "", "", "", "1", "", "", "", "", "", "", ""]
["", "", "", "2", "", "", "", "", "", "", "", "5", "", "", ""]
["", "3", "", "", "", "", "", "", "", "", "", "", "", "", ""]
["4", "", "", "", "", "", "", "", "", "", "", "", "", "", ""]]https://leetcode.com/problems/print-binary-tree/
struct Solution {
vector<vector<string>> printTree(TreeNode* root) {
int R=dep(root), C;
if(!R || !(C=col(root))) return {{}};
vector<vector<string>> res(R, vector<string>(C));
dfs(root,C/2,res,0,C/2);
return res;
}
void dfs(TreeNode* n, int j, vector<vector<string>>& res, int i, int C){
if(!n) return;
res[i][j] = to_string(n->val);
dfs(n->left, j-C/2-1, res, i+1, C/2);
dfs(n->right, j+C/2+1, res, i+1, C/2);
}
int dep(TreeNode* R){
return (!R)?0:1+max(dep(R->left), dep(R->right));
}
int col(TreeNode* R){
return (!R)?0:1+2*max(col(R->left), col(R->right));
}
};15.12 662. Maximum Width of Binary Tree
Given a binary tree, write a function to get the maximum width of the given tree. The width of a tree is the maximum width among all levels. The binary tree has the same structure as a full binary tree, but some nodes are null.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes in the level, where the null nodes between the end-nodes are also counted into the length calculation.
Example 1:
Input:
1
/ \
3 2
/ \ \
5 3 9 Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
Example 2:
Input:
1
/
3
/ \
5 3 Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).
Example 3:
Input:
1
/ \
3 2
/
5 Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).
Example 4:
Input:
1
/ \
3 2
/ \
5 9
/ \
6 7Output: 8
Explanation:The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
https://leetcode.com/problems/maximum-width-of-binary-tree
struct Solution {
int widthOfBinaryTree(TreeNode* R) {
if(!R) return 0;
queue<pair<TreeNode*, int>> q; // {node, #}
q.push({R,1});
int r=0;
while(!q.empty()){
int sz=q.size();
int x=0, y=0;
while(sz--){
pair<TreeNode*,int> t=q.front(); q.pop();
if(i==0) x=t.second; else if(i==sz-1) y=t.second;
if(t.first->left) q.push({t.first->left,t.second*2-1});
if(t.first->right) q.push({t.first->right,t.second*2});
}
r=max(r, y-x+1);
}
return r;
}
};采用heap的方法给每个点编号.用CLRS上面的方法就是1-based index.
15.13 663. Equal Tree Partition
Given a binary tree with n nodes, your task is to check if it’s possible to partition the tree to two trees which have the equal sum of values after removing exactly one edge on the original tree.
Example 1:
Input:
5
/ \
10 10
/ \
2 3Output: True
Explanation:
5
/
10Sum: 15
10
/ \
2 3Sum: 15
Example 2:
Input:
1
/ \
2 10
/ \
2 20Output: False
Explanation: You can’t split the tree into two trees with equal sum after removing exactly one edge on the tree.
https://leetcode.com/problems/equal-tree-partition
class Solution {
bool checkEqualTree(TreeNode* n, int x=0) {
if(!n) return 0;
int l=sum(n->left), r=sum(n->right);
if(n->left && l==n->val+r+x) return true;
if(n->right && l+n->val+x==r) return true;
if(n->left)
if(checkEqualTree(n->left, n->val+r+x)) return true;
if(n->right)
if(checkEqualTree(n->right, n->val+l+x)) return true;
return false;
}
int sum(TreeNode* n){
if(!n) return 0;
return n->val+sum(n->left) +sum(n->right);
}
};用递归的方法,用最简单的case想起.然后往子树走.
15.14 invertTree(Relation between DFS and Recursion)
https://leetcode.com/problems/invert-binary-tree/
class Solution(object):
def invertTree(self, root):
if root:
self.invertTree(root.left)
self.invertTree(root.right)
root.left, root.right = root.right, root.left
return root注意是后序遍历.
15.15 100. Same Tree
Given two binary trees, write a function to check if they are equal or not.
Two binary trees are considered equal if they are structurally identical and the nodes have the same value.
15.15.1 Iterative DFS
https://leetcode.com/problems/same-tree/
bool isSameTree(TreeNode* p, TreeNode* q) {
stack<pair<TreeNode*,TreeNode*>> T;
T.push({p, q});
while(!T.empty()){
auto pp = T.top(); T.pop();
if (pp.first==pp.second) continue; // both are NULL or same node
if (pp.first && pp.second && pp.first->val == pp.second->val){
T.push({pp.first->left, pp.second->left});
T.push({pp.first->right, pp.second->right});
}else return false;
}
return true;
}15.16 112. Path Sum
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.
15.17 Path Sum II(Traverse One Binary Tree)
Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1Return:
[
[5,4,11,2],
[5,8,4,5]]
https://leetcode.com/problems/path-sum-ii/
struct Solution {
vector<vector<int>> pathSum(TreeNode* root, int sum) {
vector<vector<int>> r;
vector<int> p;
int cur = sum;
dfs(root, r, p, cur);
return r;
}
void dfs(const TreeNode* root, vector<vector<int>>& r, vector<int>& p, int& cur){
if (not root) return;
int tmp = cur;
// put pair operatsion in one line to avoid missing each
cur -= root->val, p.push_back(root->val);
if (cur == 0 and not root->left and not root->right){
r.push_back(p);//// should not return without reverting stack
}else{
dfs(root->left,r,p,cur);
dfs(root->right,r,p,cur);
}
p.pop_back(), cur = tmp; // recover stack
}
};15.18 Path Sum III
https://leetcode.com/problems/path-sum-iii
You are given a binary tree in which each node contains an integer value. Find the number of paths that sum to a given value. The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes). The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.
Example:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1Return 3. The paths that sum to 8 are:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
- Algo 1: 代码量最少的递归解法
struct Solution {
int pathSum(TreeNode* root, int sum) {
if (!root) return 0;
return pathSum(root->left, sum) +
pathSum(root->right, sum) +
pathSumFromRoot(root, sum);
}
int pathSumFromRoot(TreeNode* n, int sum){
if(!n) return 0;
return (n->val == sum) +
pathSumFromRoot(n->left, sum-n->val) +
pathSumFromRoot(n->right,sum-n->val);
}
};此方法最差情况下(极度不平衡的二叉树,类似单链表)的时间复杂度为\(O(n^2)\),最好情况下(平衡二叉树)的时间复杂度为\(O(nlogn)\).
- Algo 2: DFS + Two Sum
Algo 1存在大量重复计算的问题.Algo 2通过记录遍历过程达到\(O(n)\)的时间复杂度.
https://www.deadend.me/2016/12/04/path-sum-iii
http://www.cnblogs.com/liujinhong/p/6444322.html
So the idea is similar as Two sum, using HashMap to store ( key : the prefix sum, value : how many ways get to this prefix sum) , and whenever reach a node, we check if prefix sum-target exists in hashmap or not, if it does, we added up the ways of prefix sum-target into res.
For instance : in one path we have 1,2,-1,-1,2, then the prefix sum will be: 1, 3, 2, 1, 3, let’s say we want to find target sum is 2, then we will have{2}, {1,2,-1}, {2,-1,-1,2} and {2}ways.
通过上图,我们明白了这个算法的思想.这个算法通过一个hashmap来保存这样的prefix sum信息.那么多二叉树的分叉,是否需要为每一个分支建立一个HashMap呢?我们并不需要这样做,而是采用回溯的做法,如果当前节点的所有的路径都处理完毕了,则把该节点从HashMap中删除,转而去处理别的节点.在初始的时候我们把（0,1)加入HashMap.这是为了那些curSum正好target情况的出现.
public class Solution {
public int pathSum(TreeNode root, int sum) {
HashMap<Integer, Integer> preSum = new HashMap<>();
preSum.put(0, 1);
return dfs(root, 0, sum, preSum);
}
public int dfs(TreeNode root, int curSum, int target,
HashMap<Integer, Integer> preSum) {
if(root == null) return 0;
curSum += root.val;
int res = preSum.getOrDefault(curSum-target, 0);//
int t=preSum.getOrDefault(curSum, 0) + 1;
preSum.put(curSum, t);
res += dfs(root.left, curSum, target, preSum);
res += dfs(root.right, curSum, target, preSum);
preSum.put(curSum, t-1);//回溯.把已经处理完毕的当前节点从路径中清除
return res;
}
}15.19 666. Path Sum IV
If the depth of a tree is smaller than 5, then this tree can be represented by a list of three-digits integers.
For each integer in this list:
The hundreds digit represents the depth D of this node, 1 <= D <= 4. The tens digit represents the position P of this node in the level it belongs to, 1 <= P <= 8. The position is the same as that in a full binary tree. The units digit represents the value V of this node, 0 <= V <= 9.
Given a list of ascending three-digits integers representing a binary with the depth smaller than 5. You need to return the sum of all paths from the root towards the leaves.
Example 1:
Input: [113, 215, 221]
Output: 12
Explanation:
The tree that the list represents is:
3
/ \
5 1The path sum is (3 + 5) + (3 + 1) = 12.
Example 2:
Input: [113, 221]
Output: 4
Explanation:
The tree that the list represents is:
3
\
1The path sum is (3 + 1) = 4.
https://leetcode.com/problems/path-sum-iv
struct Solution { // 6ms
int pathSum(vector<int>& ns) {
if(ns.empty()) return 0;
vector<vector<int>> fbt(5,vector<int>(9));// Full Binary Tree
int de, od, vl;
for(int i=0;i<ns.size();++i){
de=ns[i]/100, od=ns[i]%100/10, vl=ns[i]%10;
fbt[de][od] = vl + (de==1?0:fbt[de-1][(od+1)/2]);
}
const auto& v=fbt[de];
int r=accumulate(v.begin(),v.end(), 0);// last layer
for(int i=de-1;i>=0;--i)
for(int j=0;j<9;++j)
if(fbt[i][j] && fbt[i+1][2*j-1]==0 && fbt[i+1][2*j]==0)// leaf node
r+=fbt[i][j];
return r;
}
};用一个matrix来存FBT,然后从上往下遍历填充matrix．然后在往上遍历寻找leaf node算出最后结果.
数据结构用map也可以,但这题空间要求很小,所以直接用matrix.
15.20 124. Binary Tree Maximum Path Sum
Given a non-empty binary tree, find the maximum path sum. For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example 1:
Input: [1,2,3]
1
/ \
2 3Output: 6 Example 2:
Input: [-10,9,20,null,null,15,7]
-10
/ \
9 20
/ \
15 7Output: 42
https://leetcode.com/problems/binary-tree-maximum-path-sum
-10
/ \
-9 -20(from here)
/ \
-15 -7
class Solution { // T: O(N), S: O(N)
public:
int maxPathSum(TreeNode *root) {
int maxAns = INT_MIN;
dfs(root, maxAns);
return maxAns;
}
// return the max sum if root is in the critical path
// update global max
int dfs(TreeNode *root, int &global_max) {
if (root == NULL)
return 0;
int l = max(0, dfs(root->left, global_max));
int r = max(0, dfs(root->right, global_max));
global_max = max(global_max, l + r + root->val);
return root->val + max(l, r);
}
};15.21 543. Diameter of Binary Tree
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
Example:
Given a binary tree
1
/ \
2 3
/ \
4 5 Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
https://leetcode.com/problems/diameter-of-binary-tree/
分两种情况,一是该路径经过root,二是该路径不经过root :-)
struct Solution {
int diameterOfBinaryTree(TreeNode* root) {
if(!root) return 0;
return max({
diameterOfBinaryTree(root->left),
diameterOfBinaryTree(root->right),
longest_path(root->left)+longest_path(root->right) // pass through root
});
}
int longest_path(TreeNode* root){
if(!root) return 0;
return 1+max(longest_path(root->left),longest_path(root->right));
}
};15.21.2 Longest path in an undirected tree
http://www.geeksforgeeks.org/longest-path-undirected-tree/
Algorithm: Run BFS from any node to find the farthest leaf node. Label that node T. Run another BFS to find the farthest node from T. The path you found in step 2 is the longest path in the tree.
15.22 687. Longest Univalue Path
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.
Note: The length of path between two nodes is represented by the number of edges between them.
Example 1:
Input:
5
/ \
4 5
/ \ \
1 1 5Output:2
Example 2:
Input:
1
/ \
4 5
/ \ \
4 4 5Output: 2
class Solution {
public:
int longestUnivaluePath(TreeNode* root) {
if (!root) return 0;
return max({
longestUnivaluePath(root->left),
longestUnivaluePath(root->right),
f(root->left, root) + f(root->right, root)
});
}
int f(TreeNode* r, TreeNode* p){
if(!r or r->val!=p->val) return 0;
return 1+max(f(r->left,r),f(r->right,r));
}
};