Chapter 60 Bloomberg 2016
60.2 Reverse Integer
int reverse(int x) {
long long r=0;
while(x) r = r*10 + x%10, x /= 10;
return (r>INT_MAX || r<INT_MIN) ? 0 : r;
}If long long is not allowed, we can use this:
int reverse(int x){
int r = 0, p = 0;
while(x){
p = r, r = r*10 + x%10;
if (r/10!=p) return 0;
x /= 10;
}
return r;
}Python has different modulo result from C++, so you need to use abs function. Python Version:
60.3 645. Set Mismatch
The set S originally contains numbers from 1 to n. But unfortunately, due to the data error, one of the numbers in the set got duplicated to another number in the set, which results in repetition of one number and loss of another number.
Given an array nums representing the data status of this set after the error. Your task is to firstly find the number occurs twice and then find the number that is missing. Return them in the form of an array.
Example 1: Input: nums = [1,2,2,4], Output: [2,3]
https://leetcode.com/contest/leetcode-weekly-contest-42/problems/set-mismatch/
60.3.1 Algo 1: Gauss Sum
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
int n = nums.size();
vector<int> counter(n + 1);
int expect = n * (n + 1) / 2;
int actual = accumulate(nums.begin(), nums.end(), 0);
for ( int i : nums ) {
if ( 1 == counter[i] )
return {i, expect - actual + i};
++counter[i];
}
}
};test case: {2,3,3,4,5,6}, {1,2,2,3,4,5,6}
60.4 Missing Number in Unsorted Arithmetic Series
https://en.wikipedia.org/wiki/Arithmetic_progression
Ideas:
- Sort - \(O(NLogN)\)
- Gauss Sum - \(O(N)\) (overflow)
- XOR Trick - \(O(N)\)
- Geometric Sequence Sum -\(O(NK)\) (overflow)
60.4.1 Missing 1 number
https://leetcode.com/problems/missing-number/
Note: \(r=0\) because \(0 \wedge x == x\)
60.4.2 Missing 2 number
In the following two sequences, A has two missing numbers: 3 and 9.
\[A = 1, 2, p, 4, 5, 6, 7, 8, p, 10\>\\B = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\]
where placeholder \(p\) is any value except 3 and 9. \(p\) doesn’t matter as two same numbers have no impact in xor trick, and it can be nothing.
Then \[A \wedge B = 3\wedge 9 = 10=0b10\underline{1}0\]
According to the second from the last bit, we can split:
\(A\) into \(A_1=1,4,5,8\) and \(A_2=2,6,7,10\)
\(B\) into \(B_1=1,4,5,8,9\) and \(B_2=2,3,6,7,10\)
Then we can get missing numbers 3 and 9 using missingNumber(\[A_1,B_1\]) and missingNumber(\[A_2,B_2\]).
60.4.3 Missing k number
60.4.3.1 Case 1:
In the following two sequences, A has two missing numbers: x = 3 and y = 9. \[A = 1, 2, 4, 5, 6, 7, 8, 10\>\\B = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\]
We have:
(1). \(A \wedge B =x \wedge y=10=R\)
(2). \(\sum A[i] - \sum B[i] =x+y=12=S1\)
(3). \(\sum A[i]^2 - \sum B[i]^2=x^2+y^2 =90=S2\)
- Get \(x\) and \(y\) by solving simultaneous equations (1) and (2)
If \(x\wedge y= R, x+y=S, x, y \in \mathbb{Z}^+_0, x\neq y\) and \(R\) and \(S\) are constants, is there a unique solution?
- Get \(x\) and \(y\) by solving simultaneous equations (2) and (3)
60.4.3.2 Case 2 (with placeholders):
In the following two sequences, A has two missing numbers: x = 3 and y = 9.
\[A = 1, 2, p, 4, 5, 6, 7, 8,p,10\>\\B = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\]
(1). \(\sum A[i] - \sum B[i] =x+y-2p=S_1\)
(2). \(\sum A[i]^2 - \sum B[i]^2=x^2+y^2-2p^2 =S_2\)
(3). \(\sum A[i]^3 - \sum B[i]^3=x^3+y^3-2p^3 =S_3\)
We can get x, y, p by solving the three simultaneous equations.
60.8 deadlock
bank account transfer - how to avoid deadlock?
transfer(account from, account to, double amount)
transfer(a,b,100.)
transfer(b,a,100.)Just sort from and to and make sure the locking order is the same in the two function calls.
60.9 Histogram Iterator
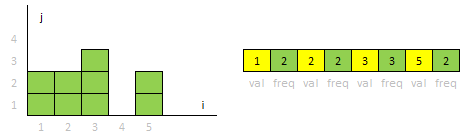
#include <henry.h>
//{1 1 2 2 3 3 3 5 5}
//{1 2 2 2 3 3 5 2}
struct myiterator{
const vector<int>& v;
int i; // idx of counter
int j; // val of counter
myiterator(const vector<int>& vi):v(vi),i(1),j(v[i]){}
int next(){
if(j>0){
--j;
}else{
++++i;
if (i>=v.size()){ throw "stop";}
j=v[i]-1;
}
return v[i-1];
}
bool hasNext(){
return i<v.size()-1 || ((i==v.size()-1)&&j>0);
}
};
int main(){
vector<int> vi= {1, 2, 2, 2, 3, 3, 5, 2};
myiterator it(vi);
while (it.hasNext()){
cout << it.next() << endl;
}
return 0;
}这道题有Bug,如果输入有{9,0}就会出错.
60.10 Best Time to Buy and Sell Stock (Once)
http://www.lintcode.com/en/problem/best-time-to-buy-and-sell-stock/
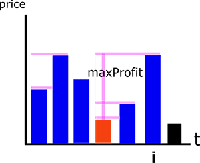
int maxProfit(vector<int> &prices) {// O(N)
int cur_min = INT_MAX, r = 0;
for(int i: prices)
cur_min = min(cur_min, i), r = max(i - cur_min, r);
return r;
}This is just the opposite of calculating max drawdown!
Max Drawdown
http://www.investopedia.com/terms/m/maximum-drawdown-mdd.asp
60.11 Best Time to Buy and Sell Stock (Unlimited Times)
http://www.lintcode.com/en/problem/best-time-to-buy-and-sell-stock-ii/

Note:
- You can sell and buy the same stock at one day, but transaction mean buy + sell.
- For the result of \(adjacent\_difference(\cdot)\), the first element is not a difference!
http://en.cppreference.com/w/cpp/algorithm/adjacent_difference
60.12 Best Time to Buy and Sell Stock (At Most Two Transactions)
http://www.lintcode.com/en/problem/best-time-to-buy-and-sell-stock-iii/
http://blog.csdn.net/fightforyourdream/article/details/14503469
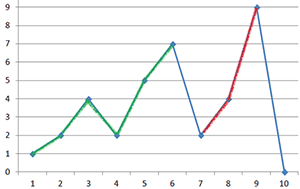
int maxProfit(vector<int> &prices) {// O(N)
const int L = prices.size();
if (L<=1) return 0;
int l[L]={0}, r[L]={0}, mi=prices[0], ma=prices[L-1], i=1, R=0;
for(; i < L; ++i)
l[i] = max(l[i-1], prices[i] - mi), mi = min(prices[i], mi);
for(i = L-2; i >= 0; --i)
r[i] = max(r[i+1], ma - prices[i]), ma = max(ma, prices[i]);
for(i = 0; i < L; ++i)
R = max(R, l[i] + r[i]);
return R;
}数组l[i]记录了price[0..i]的最大profit,数组r[i]记录了price[i..n]的最大profit.
60.13 Best Time to Buy and Sell Stock (At Most K Transactions)
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/
https://www.youtube.com/watch?v=oDhu5uGq_ic


class Solution {
int maxProfit_unlimitedTransaction(vector<int> &prices) {// O(N)
int r = 0;
for (int i = 1; i<prices.size(); ++i) // starting from 1
if(prices[i]>prices[i-1]) r+=prices[i]-prices[i-1];
return r;
}
public:
int maxProfit(int k, vector<int>& p) { // T: O(K*N^2)
const int L = p.size();
if (L <= 1) return 0;
if (k >= L-1) return maxProfit_unlimitedTransaction(p);
vector<vector<int>> r(k + 1, vector<int>(L+1));
for (int i=1; i<k+1; ++i) // K
for (int j=1; j<L; ++j) { // N
r[i][j] = r[i][j-1];// No transaction in the last day
for (int k=0; k<j; ++k) // O(N) there is a transaction in the last day
r[i][j] = max(r[i][j], r[i-1][k]+p[j]-p[k]);
}
return r[k][L-1];
}
};60.13.1 Optimize Time

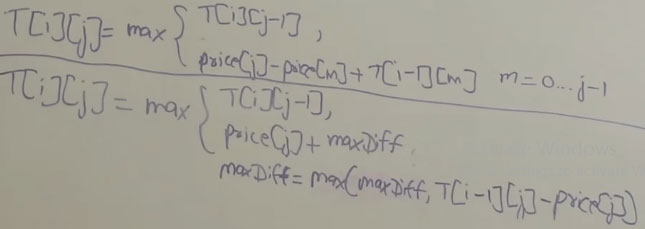
int maxProfit(int k, vector<int>& prices) {// T: O(NK), S:O(NK)
int L = prices.size();
if (L <= 1) return 0;
if (k >= L-1) return maxProfit_unlimitedTransaction(prices);
vector<vector<int>> r(k + 1, vector<int>(L));
for (int i = 1; i<k + 1; ++i) { // O(K)
int ma = 0 - prices[0];
for (int j = 1; j<L; ++j) { // O(N)
r[i][j] = max(r[i][j - 1], prices[j] + ma);
ma = max(ma, r[i - 1][j] - prices[j]);
}
}
return r[k][L - 1];
}60.13.2 Optimize Space
Like Edit Distance problem, we can optimize the space complexity from \(O(NK)\) to \(O(N)\) using rolling array.
int maxProfit(int k, vector<int>& prices) {
int L = prices.size();
if (L <= 1) return 0;
if (k >= L-1) return maxProfit_unlimitedTransaction(prices);
vector<int> tmp(L, 0), r(L, 0);
for (int i = 1; i<k + 1; ++i) { // O(K)
int ma = 0 - prices[0];
for (int j = 1; j<L; ++j) { // O(N)
r[j] = max(r[j - 1], prices[j] + ma);
ma = max(ma, tmp[j] - prices[j]);
}
swap(tmp, r);
}
return tmp[L - 1];
}60.14 Best Time to Buy and Sell Stock with Cooldown
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/
Note the transaction time is unlimited.
http://www.cnblogs.com/grandyang/p/4997417.html
https://leetcode.com/discuss/71354/share-my-thinking-process