Chapter 25 Dynamic Programming
The most crucial part of Dynamic Programming is to get the formula. It tests the math modeling ability of candidates.
http://ryanleetcode.blogspot.com/2015/07/blog-post_16.html
Recurrence Equation or Transition Equation
Must use known state to calculate unknown state.
25.1 91. Decode Ways
A message containing letters from A-Z is being encoded to numbers using the following mapping:
'A' -> 1
'B' -> 2
...
'Z' -> 26Given an encoded message containing digits, determine the total number of ways to decode it.
For example, Given encoded message “12”, it could be decoded as “AB” (1 2) or “L” (12).
The number of ways decoding “12” is 2.
Link:  https://leetcode.com/problems/decode-ways/
https://leetcode.com/problems/decode-ways/
struct Solution {
int numDecodings(string s) {
int L=s.size();
if(L==0 or s[0]=='0') return 0;
vector<int> v(L+1);
v[0]=v[1]=1;
for(int l=2; l<=L; ++l){
int t=stoi(s.substr(l-2,2));
v[l]=(s[l-1]=='0'?0:v[l-1]) + ((t>=10 and t<=26)?v[l-2]:0);
}
return v[L];
}
};注意: 0不能代表任何letter.
Reference: http://bit.ly/2eygk8J, http://bit.ly/2ey5Vu1, http://bit.ly/2eyjfhZ
25.2 639. Decode Ways II
A message containing letters from A-Z is being encoded to numbers using the following mapping way:
'A' -> 1
'B' -> 2
...
'Z' -> 26Beyond that, now the encoded string can also contain the character ‘*’, which can be treated as one of the numbers from 1 to 9. Given the encoded message containing digits and the character ‘*’, return the total number of ways to decode it.
Also, since the answer may be very large, you should return the output mod 10^9 + 7.
Example 1:
Input: "*"
Output: 9
Explanation: The encoded message can be decoded to the string: "A", "B", "C", "D", "E", "F", "G", "H", "I".Example 2:
Input: "1*"
Output: 9 + 9 = 18Note:
The length of the input string will fit in range [1, 105].
The input string will only contain the character '*' and digits '0' - '9'.https://leetcode.com/problems/decode-ways-ii/
A common function:
int getnum(const string& s){
if(s.size()==1){ // when s is one-digit representation
if(s[0]=='0') return 0; else if(isdigit(s[0])) return 1; if(s=="*") return 9;
} else if(s.size()==2){ // when s is two-digit representation
if(isdigit(s[0]) && isdigit(s[1])){
int t=stoi(s);
if(10<=t and t<=26) return 1; else return 0;
}else{
if(s=="**") return 15; // 9+6, (11-19,21-26), "*" cannot be zero!
else if(s[0]=='*') return '7'<=s[1]?1:2;
else if(s[0]=='1') return 9;
else if(s[0]=='2') return 6;
else return 0;
}
}
return 0;
}- Algo 1: DP Top Down
struct Solution {
vector<int> dp;
int numDecodings(string s) {
int L=s.size();
dp=vector<int>(L+1,-1);
return getdp(s,L);
}
long long int getdp(string s, int l){
if(dp[l]>0) return dp[l];
if(l<=1) return dp[l]=getnum(s.substr(0,1));
if(l==2) return dp[l]=(getnum(s.substr(0,2)) + getnum(s.substr(0,1)) * getnum(s.substr(1,1)));
return dp[l] = (getdp(s,l-2)*getnum(s.substr(l-2,2))+ getdp(s,l-1)*getnum(s.substr(l-1,1)))%1000000007;
}
};This one should work fine, but I got MLE. There is a super big input which triggered MLE. So the only way is to use iterative way.
- Algo: DP Bottom Up
T:\(O(N)\), S:\(O(N)\)
vector<long long int> dp;
int numDecodings(string s){
int L=s.size();
if(L==0 or s[0]=='0') return 0;
dp=vector<long long int>(L+1,1);
if(s[0]=='*') dp[1]=9; // if digit, =1; else if star, =9.
for(int l=2;l<=L;++l){
long long int j=dp[l-2]*getnum(s.substr(l-2,2));
long long int k=dp[l-1]*getnum(s.substr(l-1,1));
dp[l] = (j+k)%1000000007; // (int)1e9+7
}
return dp.back();
}Use rolling number to optimize space complexity: T:\(O(N)\), S:\(O(1)\)
int numDecodings(string s){
int L=s.size();
long long int r=1, pp=1, p=1;
if(s[0]=='*') p=9; else if(s[0]=='0') p=0;
if(L==1) return p;
for(int l=2; l<=L; ++l){
long long int j=pp*getnum(s.substr(l-2,2));
long long int k=p*getnum(s.substr(l-1,1));
r = (j+k)%1000000007;
pp=p, p=r;
}
return r%1000000007;
}25.3 10. Regular Expression Matching
Implement regular expression matching with support for ‘.’ and ‘*’.
‘.’ Matches any single character.
‘*’ Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
The function prototype should be: bool isMatch(const char *s, const char *p)
Some examples:
isMatch(“aa”,“a”) → false
isMatch(“aa”,“aa”) → true
isMatch(“aaa”,“aa”) → false
isMatch(“aa”, “a*”) → true
isMatch(“aa”, “.*”) → true
isMatch(“ab”, “.*”) → true
isMatch(“aab”, “c*a*b”) → true
https://leetcode.com/problems/regular-expression-matching
class Solution {
public:
bool isMatch(string s, string p) {
if (p.empty())
return s.empty();
if ('*' == p[1])
// x* matches empty string or at least one character: x* -> xx*
// *s is to ensure s is non-empty
return isMatch(s, p.substr(2)) ||
!s.empty() &&
(s[0] == p[0] || '.' == p[0]) && isMatch(s.substr(1), p);
else
return !s.empty() &&
(s[0] == p[0] || '.' == p[0]) &&
isMatch(s.substr(1), p.substr(1));
}
};25.4 Unique Binary Search Trees
Catalan Number
 https://leetcode.com/problems/unique-binary-search-trees-ii/
https://leetcode.com/problems/unique-binary-search-trees-ii/
 https://leetcode.com/problems/unique-binary-search-trees/
https://leetcode.com/problems/unique-binary-search-trees/
http://blog.csdn.net/hackbuteer1/article/details/7450250
Enumerative Combinatorics V1: http://math.mit.edu/~rstan/ec/ec1.pdf
https://en.wikipedia.org/wiki/Catalan_number
Chinese: https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%A1%94%E5%85%B0%E6%95%B0
25.5 139. Word Break I
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words. You may assume the dictionary does not contain duplicate words.
For example, given
s = "leetcode",
dict = ["leet", "code"].Return true because “leetcode” can be segmented as “leet code”.
UPDATE (2017/1/4):
The wordDict parameter had been changed to a list of strings (instead of a set of strings). Please reload the code definition to get the latest changes.
 https://leetcode.com/problems/word-break/
https://leetcode.com/problems/word-break/
25.5.1 Algo 1: Recursion
class Solution {
public:
bool wordBreak(string s, vector<string>& ws) {
set<string> ss;
for_each(ws.begin(), ws.end(), [&ss](string& t){ss.insert(t);});
return rec(s, 0, ss);
}
bool rec(string& s, int h, set<string>& ss){
for(int i=h;i<s.size();i++){
string t=s.substr(h, i-h+1);
if(ss.count(t))
if(i==s.size()-1 || rec(s,i+1,ss)) return true;
}
return false;
}
};Got TLE.
25.6 140. Word Break II
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. You may assume the dictionary does not contain duplicate words.
Return all such possible sentences.
For example, given
s = "catsanddog",
dict = ["cat", "cats", "and", "sand", "dog"].A solution is [“cats and dog”, “cat sand dog”].
UPDATE (2017/1/4):
The wordDict parameter had been changed to a list of strings (instead of a set of strings). Please reload the code definition to get the latest changes.
 https://leetcode.com/problems/word-break-ii
https://leetcode.com/problems/word-break-ii
class Solution {
unordered_map<string, vector<string>> m; //cache
vector<string> rec(string& s, unordered_set<string>& dict) {
if(m.count(s)) return m[s]; //take from cache directly
vector<string> result;
if(dict.count(s)) //the whole string is a word
result.push_back(s);
for(int i=1;i<s.size();++i){
string second=s.substr(i); // second part of string
if(dict.count(second)){
string first=s.substr(0,i); // first part of string
auto t=rec(first, dict);
vector<string> prev=combine(second, t);
result.insert(result.end(), prev.begin(), prev.end());// merge two vectors
}
}
return m[s]=result; //memoization not memorization
}
vector<string> combine(string& word, vector<string>& prev){
for(int i=0;i<prev.size();++i) prev[i]+=" "+word;
return prev;
}
public:
vector<string> wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> st(wordDict.begin(), wordDict.end());
return rec(s, st);
}
};25.7 Edit Distance (Levenshtein distance)
Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)
You have the following 3 operations permitted on a word:
a) Insert a character
b) Delete a character
c) Replace a characterhttps://en.wikipedia.org/wiki/Levenshtein_distance
 https://leetcode.com/problems/edit-distance/
https://leetcode.com/problems/edit-distance/
X - Add
Y - Del
Z - Rep25.7.1 Analysis with Sample Cases
eat and tea
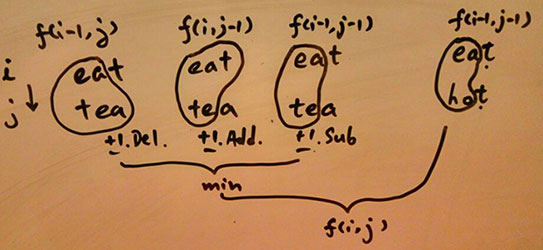
\(f('e','t') = 1\) by Z
\(f('ea','te') = 2\) by XY or ZZ
What is \(f('eat','tea')\)?
Case 1: \(f('ea','te')\) = 2 by ZZ or XY
Case 2: \(f('ea','tea')\) = 1 by X
Case 3: \(f('eat','te')\) = 3 by ZZY or XYY
Here we can get recurrence equation:
\[f(i,j)= \begin{cases} min(f(i-1,j-1),f(i-1,j),f(i,j-1))+1, & A[i-1] \neq B[j-1] \\ f(i-1,j-1), & A[i-1] = B[j-1] \\ \end{cases} \]
where \(i, j \in \mathbb{Z^{+}_0}\), \(i,j\) means the length of string \(A\) and \(B\) respectively.
In this case, we get: \(f('eat','tea') = 2\) by XY
25.7.2 Boundary Condition
Boundary Condition are seed values we cannot use recurrence equation to calculate. Instead, we use them to bootstrap other values. By observation, we know \(f[i][0]=i\) by Y and \(f[0][j]=j\) by X, so \(f[0][1]\) = 1 and \(f[1][0]\) = 1. We also know:
\[f(1,1)= \begin{cases} min(f(0,0),f(0,1),f(1,0))+1, & A[0] \neq B[0] \\ f(0,0), & A[0] = B[0] \\ \end{cases} \] That is: \[f(1,1)= \begin{cases} min(f(0,0),1,1)+1, & A[0] \neq B[0] \\ f(0,0), & A[0] = B[0] \\ \end{cases} \]
We know \(f(0,0)\) must be equal to \(0\).
So the boundary conditions are: \(f[i][0]=i\) and \(f[0][j]=j\) where \(i, j \in \mathbb{Z^{+}_0}\)
Note: As 0-length string is considered, the matrix should be size of \(M+1, N+1\), where \(M=A.size(), N=B.size()\)
25.7.3 Coding
struct Solution {
int minDistance(string word1, string word2) {//T: O(MN) ES: O(MN)
int M = word1.size(), N = word2.size();
vector<int> tmp(N + 1);
iota(tmp.begin(), tmp.end(), 0);
vector<vector<int>> B(M + 1, tmp);
for (int i = 0; i<M + 1; ++i) B[i][0] = i;// boundary conditions
for (int i = 1; i<M + 1; ++i)// recurrence equation
for (int j = 1; j<N + 1; ++j)
B[i][j] = (word1[i - 1] == word2[j - 1]) ? B[i - 1][j - 1] : \
min(min(B[i - 1][j - 1], B[i - 1][j]), B[i][j - 1]) + 1;
return B[M][N];
}
};
25.7.4 Optimization Space with Rolling Array
We can see, from the code above, the table \(B\) is updated row by row. The current row has relation with only its direct upper row. The table is not reused, so we can optimize the space from \(O(MN)\) to \(O(N)\).
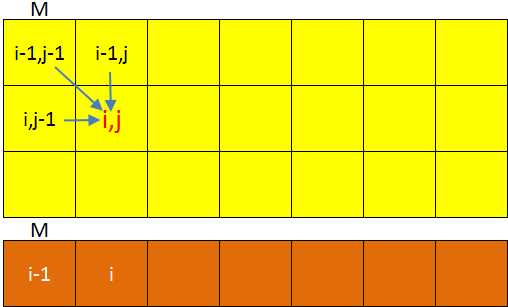
现在要节约空间把一个矩阵压缩为一个array,一定要用临时变量.更新M[i][j]的时候,M[i-1][j-1]和M[i-1][j]都要用临时变量保存起来.
struct Solution {//T: O(ROWxCOL) ES:O(COL)
int minDistance(string word1, string word2) {
int R = word1.size(), C = word2.size();
vector<int> M(C + 1);
iota(M.begin(), M.end(), 0);// boundary conditions
for (int i = 1; i<R + 1; ++i) {// recurrence equation
int prev = M[0]; // 保存M[i-1][j-1]
M[0] = i; // 初始化boundary condition
for (int j = 1; j<C + 1; ++j) {
int tmp = M[j];////!!!!back up prev
M[j] = (word1[i - 1] == word2[j - 1]) ? prev :
min(min(M[j - 1], M[j]), prev) + 1;
prev = tmp;
}
}
return M[C];
}
};可以看到用临时变量交换数据的pattern,类似reverse linked list.
25.8 97. Interleaving String
Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
For example, Given: s1 = “aabcc”, s2 = “dbbca”,
When s3 = “aadbbcbcac”, return true.
When s3 = “aadbbbaccc”, return false.
https://leetcode.com/problems/interleaving-string/
// A simple recursive function to check whether C is an interleaving of A and B
bool isInterleaved(char *A, char *B, char *C){
// Base Case: If all strings are empty
if (!(*A || *B || *C))
return true;
// If C is empty and any of the two strings is not empty
if (*C == '\0')
return false;
// If any of the above mentioned two possibilities is true,
// then return true, otherwise false
return ( (*C == *A) && isInterleaved(A+1, B, C+1))
|| ((*C == *B) && isInterleaved(A, B+1, C+1));
}2D DP:
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int m=s1.size(), n=s2.size(), l=s3.size();
if(m+n!=l) return false;
vector<vector<bool>> dp(m+1,vector<bool>(n+1));
dp[0][0]=1;
for(int i=1;i<=m;i++) dp[i][0]=s1.substr(0,i)==s3.substr(0,i);
for(int j=1;j<=n;j++) dp[0][j]=s2.substr(0,j)==s3.substr(0,j);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
if(s3[i+j-1]==s1[i-1]&&s3[i+j-1]==s2[j-1]) // BUG
dp[i][j] = dp[i-1][j]||dp[i][j-1];
else if(s3[i+j-1]==s1[i-1]) dp[i][j] = dp[i-1][j];
else if(s3[i+j-1]==s2[j-1]) dp[i][j] = dp[i][j-1];
else dp[i][j]=0;
}
}
return dp[m][n];
}
};After optimization:
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int m = s1.length();
int n = s2.length();
int p = s3.length();
if (m + n != p) return false;
vector<bool> dp(n + 1);
for (int j = 0; j <= n; j++)
dp[j] = s2.substr(0, j)==s3.substr(0, j);
for (int i = 1; i <= m; i++){
dp[0] = s1.substr(0, i)==s3.substr(0, i);
for (int j = 1; j <= n; j++)
dp[j] = (dp[j] && s3[i+j-1]==s1[i-1]) || (dp[j-1] && s3[i+j-1]==s2[j-1]);
}
return dp[n];
}
};25.9 Distinct Subsequences
Given a string S and a string T, count the number of distinct subsequences of S which equals T.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ACE” is a subsequence of “ABCDE” while “AEC” is not).
Here is an example: S = “rabbbit”, T = “rabbit”, Return 3.
https://leetcode.com/problems/distinct-subsequences/
http://www.geeksforgeeks.org/count-distinct-occurrences-as-a-subsequence/
25.9.1 Count distinct occurrences as a subsequence
Given a string, find count of distinct subsequences of it(including empty string).
Examples:
Input : str = “gfg”
Output : 7
The seven distinct subsequences are "“,”g“,”f“,”gf“,”fg“,”gg" and “gfg”
Input : str = “ggg”
Output : 4
The six distinct subsequences are "“,”g“,”gg" and “ggg”
http://www.geeksforgeeks.org/count-distinct-subsequences/
#include <bits/stdc++.h>
using namespace std;
const int MAX_CHAR = 256;
int countSub(string str){ // Returns count of distinct sunsequences of str.
// Create an array to store index of last
vector<int> last(MAX_CHAR+1, -1);
// Length of input string
int n = str.length();
// dp[i] is going to store count of distinct subsequences of length i.
int dp[n+1];
dp[0] = 1; // Empty substring has only one subsequence
// Traverse through all lengths from 1 to n.
for (int len=1; len<=n; len++) {
// Number of subsequences with substring str[0..i-1]
dp[len] = 2*dp[len-1];
// If current character has appeared before, then remove all subsequences
// ending with `previous` occurrence.
if (last[str[len-1]] != -1)
dp[len] -= dp[last[str[len-1]]];
last[str[len-1]] = (len-1); // Mark occurrence(index) of current character
}
return dp[n];
}25.10 Longest Increasing Subsequence(LIS)
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given [10, 9, 2, 5, 3, 7, 101, 18],
The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in \(O(n^2)\) complexity.
Follow up: Could you improve it to \(O(n log n)\) time complexity?
 https://leetcode.com/problems/longest-increasing-subsequence/
https://leetcode.com/problems/longest-increasing-subsequence/
http://www.cnblogs.com/Seiyagoo/p/3389501.html
structical problem!

25.10.1 Algo 1 - LCS
Sort the given sequence in non-decreasing order and apply LCS to the given and sorted list. And this will give both the LIS lenght and LIS.
Check LCS
25.10.2 Algo 2 - DP
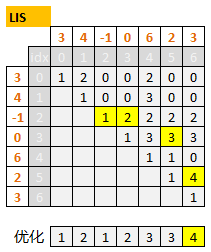
25.10.2.1 Analysis:
In Fibonacci series, new node has relation with two previous nodes. Here the new node has relation with all the previous nodes. This is pretty much like the wood cut problem in CLRS. You have to use two loops.
Note: The dp array in this problem doesn’t store final result. It stores intermediate result, so that we have to use max_element before return.
25.10.2.2 Base Case: Easy Part, skip…
dp[x] = max(dp[x], dp[y] + 1) where y < x and nums[y] < nums[x]struct Solution {
int lengthOfLIS(vector<int>& nums) {
if(nums.empty()) return 0;
vector<int> dp(nums.size(), 1);
for(int i=1; i<nums.size(); ++i) // [2,5,3,7,101,18]
for(int j=i-1; j>=0; --j)
if (nums[i]>nums[j])
dp[i] = max(dp[j]+1, dp[i]); // cannot be optimized?
return *max_element(dp.begin(), dp.end());
}
};25.10.4 Patience Sort(Improved for duplicates)
http://yzmduncan.iteye.com/blog/1546503
http://stackoverflow.com/questions/6129682/longest-increasing-subsequenceonlogn
To maintain a monotonically increasing sequence!!! Sounds familiar with \(O(1)\) MaxQ (http://www.quant365.com/post/93/).
Array算法之Longest increasing subsequence (LIS) 今日在复习Longest increasing subsequence (LIS)的时候在wiki看到一个算法复杂度居然只有nlogn,但是wiki没有讲的太明白,然后又到万能的google一搜索,在princeton讲义pdf学到一个绝逼的算法,我和我的小伙伴都惊呆了. 玩过接龙poker的人都知道接龙的greedy 算法吧,这算法就是用接龙greedy 算法进化而来.
greedy 算法就是把牌放在最左边并且符合条件的pile
如果牌数字依次是: 6, 3, 5, 10, 11, 2, 9, 14, 13, 7, 4, 8, 12
6 5 10 11 14
3 4 9 8 13
2 7 12这么一看是不是觉得距离获得LIS 不远了,还有一个tricky的地方是在加入每一个牌的时候要保留一个指向前面一个pile最顶端牌的指针,如图:
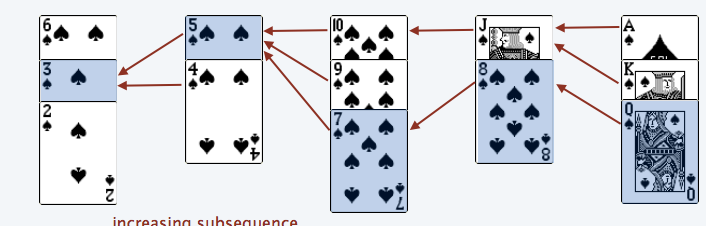
这样可以顺指针找到lis了.在找leftmost pile的时候用binary search可以把复杂度降低到\(nlogn\)!!
int lengthOfLIS(vector<int>& nums) {
set<int> st;
set<int>::iterator it;
for (int i: nums) {
/*// Also OK!
if (st.count(i)) continue;// for duplicates
it = st.insert(i).first;
if (++it != st.end()) st.erase(it);
*/
it = st.lower_bound(i);
if (it != st.end())
st.erase(it);
st.insert(i);
}
return st.size();
}Let’s assume we use them to search for 2 in the following collections. The arrows show what iterators the two would return:
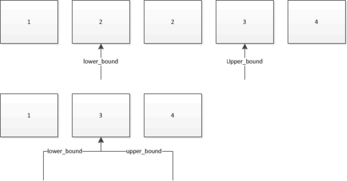
http://stackoverflow.com/questions/23554509/rationale-for-stdlower-bound-and-stdupper-bound
http://en.cppreference.com/w/cpp/container/set/lower_bound
25.11 673. Number of Longest Increasing Subsequence
Given an unsorted array of integers, find the number of longest increasing subsequence.
Example 1: Input: [1,3,5,4,7]; Output: 2
Explanation: The two longest increasing subsequence are [1, 3, 4, 7] and [1, 3, 5, 7].
Example 2: Input: [2,2,2,2,2]; Output: 5
Explanation: The length of longest continuous increasing subsequence is 1, and there are 5 subsequences’ length is 1, so output 5.
Note: Length of the given array will be not exceed 2000 and the answer is guaranteed to be fit in 32-bit signed int.
https://leetcode.com/problems/number-of-longest-increasing-subsequence
求number of path,就是求leaf node的个数. 这个方法好似求树的leaf node的个数:
int d[2000][2];
struct Solution { // 32ms
int findNumberOfLIS(vector<int>& nums) {
int i,j,k,n,ma,ans=0;
n=nums.size();
ma=0;
for (i=0;i<n;i++){
d[i][0]=1/*index*/, d[i][1]=1/*number of leaf nodes*/;
for (j=0;j<i;j++){
if (nums[j]<nums[i]){
if(d[j][0]+1 > d[i][0]){ // a new max value
d[i][0]=d[j][0]+1;
d[i][1]=d[j][1];
}else if(d[j][0]+1 == d[i][0]){ // equal, just update number
d[i][1]+=d[j][1];
}
}
}
if (d[i][0]>ma) ma=d[i][0];
}
for (i=0;i<n;i++)
if (d[i][0]==ma)
ans+=d[i][1];
return ans;
}
};这个方法采用DFS,track information of previous index,用它不但可以求个数,还可以打印出所有的最长的IS:
struct data {
int len;
vector<int> from; // from which index
};
struct Solution { // 65ms
int findNumberOfLIS(vector<int>& nums) {
int L = nums.size();
if (L == 0) return 0;
vector<data> dp(L);
for (auto& e : dp) e.len = 1;
for (int i = 1; i<L; ++i) {
for (int j = 0; j < i; ++j) {
if (nums[i]>nums[j]) {
if (dp[j].len + 1 >= dp[i].len) {
if (dp[j].len + 1 > dp[i].len)
dp[i].from.clear();
dp[i].from.push_back(j);
dp[i].len = dp[j].len + 1;
}
}
}
}
int mx = 0;
vector<int> midx;
for (int i = 0; i<L; ++i) { // put ALL max values into midx
if (dp[i].len>mx)
midx = {}, midx.push_back(i), mx = dp[i].len;
else if (dp[i].len == mx)
midx.push_back(i);
}
int r = 0;
for (int i : midx)
dfs(dp, i, r);
return r;
}
void dfs(vector<data>& dp, int i, int& r) {
if (dp[i].len == 1){
r++; return;
}
for (int k : dp[i].from)
dfs(dp, k, r);
}
};25.12 646. Maximum Length of Pair Chain
You are given n pairs of numbers. In every pair, the first number is always smaller than the second number.
Now, we define a pair (c, d) can follow another pair (a, b) if and only if b < c. Chain of pairs can be formed in this fashion.
Given a set of pairs, find the length longest chain which can be formed. You needn’t use up all the given pairs. You can select pairs in any order.
Example 1: Input: [[1,2], [2,3], [3,4]]; Output: 2; Explanation: The longest chain is [1,2] -> [3,4]
https://leetcode.com/problems/maximum-length-of-pair-chain
struct Solution {
vector<int> dp_;
int findLongestChain(vector<vector<int>>& p) {
sort(p.begin(), p.end(), [](vector<int>& x, vector<int>& y){
return x[1]<y[1];});
int L=p.size();
dp_.resize(L+1);
dp_[1]=1;
while(L) dp(p, L--);
return *max_element(dp_.begin(), dp_.end());
}
int dp(vector<vector<int>>& p, int i){ // 注意这里i是长度
if(dp_[i]!=0) return dp_[i];
for(int j=i-2;j>=0;--j)
if(p[i-1][0] > p[j][1])
dp_[i]=max(dp(p,j+1)+1,dp_[i]); // j是index,所以要j+1
return dp_[i]=max(1, dp_[i]);
}
};这道题是一个interval版本的LIS问题. DP常出bug的地方是index和长度傻傻分不清.
 其实这题最优是用greedy:
其实这题最优是用greedy:
25.13 334. Increasing Triplet Subsequence
https://leetcode.com/problems/increasing-triplet-subsequence/
题目大意是判断所给的数组中是否存在长度为3的递增序列.
最常规的办法应该是两层循环,逐个判断.时间复杂度较高.还有一种比较巧妙的办法,维护两个距离最近的递增序列,如果能找到第三个则返回true.设置一个small,一个big,small<big.如果能找到一个不小于small和big的就返回true.时间复杂度为\(O(N)\)
public struct Solution {
public boolean increasingTriplet(int[] nums) {
if(nums == null || nums.length < 3)
return false;
int small = Integer.MAX_VALUE, big = Integer.MAX_VALUE;
for(int value : nums) {
if(value <= small)
small = value;
else if(value <= big)
big = value;
else
return true;
}
return false;
}
}25.14 312. Burst Balloons
Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.
Find the maximum coins you can collect by bursting the balloons wisely.
Note:
(1) You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
(2) 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
Example:
Given [3, 1, 5, 8]
Return 167
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167 https://leetcode.com/problems/burst-balloons/
https://leetcode.com/problems/burst-balloons/
先试图找找规律:
如果是两个数字,总是burst最小的那个,结果是两数乘加上较大的那个数. 如果是三个数字,比如358,如果先burst最小的3,结果(15+48)不如burst中间的5大(120+24+8).再比如198,如果先burst最小的1得到9+72+9,先burst中间的9得到72+16,又是先burst最小的大.
所以看起来和数字的大小和位置都没有绝对的关系.复杂度一定是NP.所以只能考虑动态规划.
DP Bottom up analysis:
f(3)=3 f(31) = 6_3 如果后面加一个5,even if 315按照相同的顺序burst 31,得到的结果也不同. f(315) = 如果31最后爆3,结果是?;如果31最后爆1,?
DP Top down analysis:
f(3…5) is known as C f(3…58)?
Divide-Conquer:
终于DC看起来比较合适.以\(f()\)表示burstballon算法.以一个长度为25的数组A为例.
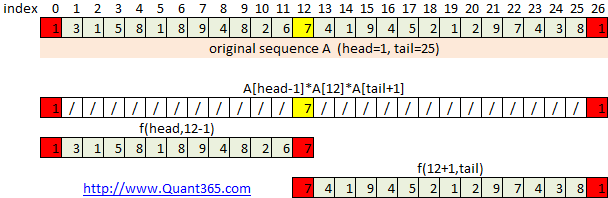
先在原数组前后加一个1,然后对A[1](head=1)到A[25](tail=25)做循环. 这个设计很重要,我们在每次divide之后仍然可以复用原数列!
如图,假设黄点7是最后一个被burst的,那么结果\(f(head,tail)\)一定等于下面三段结果之和
\[A[head-1]*A[12]*A[tail+1] + f(head,12-1) + f(12+1,tail)\]
从A[1]到A[25]中任何一个都有可能是最后被burst的,所以结果就是
\[f(head,tail)=max(A[head-1]*A[i]*A[tail+1] + f(head, i-1) + f(i+1,tail))\]
where \[head \le i \le tail\]
注意这个divide conquer和普通的有点不同,divide之后,两个边缘点很可能不是1了.
\(f(head,tail)\)其实是左右边缘点分别是1,1的时候burstballon算法的值.
\(f(head,12-1)\)则是左右边缘点分别是1,7的时候burstballon算法的值.
\(f(12+1,tail)\)则是左右边缘点分别是7,1的时候burstballon算法的值.
只不过我们复用了原数列所以并没有显示的指出这点. 如果用分布式计算的方法来解决这个问题,必须把两个边缘点的值传到相应的节点,不必传整个原始数列A.
http://www.cnblogs.com/grandyang/p/5006441.html
https://www.youtube.com/watch?v=IFNibRVgFBo
http://bookshadow.com/weblog/2015/11/30/leetcode-burst-balloons/
struct Solution { // 16 lines, 52 ms
int maxCoins(vector<int>& nums) {
nums.insert(nums.begin(), 1), nums.push_back(1);
vector<vector<int>> dp(nums.size(),vector<int>(nums.size(),0));
return bb(nums, dp, 1, nums.size()-2);
}
int bb(vector<int>& ns, vector<vector<int>>&dp, int head, int tail){
if(head>tail) return 0; //!!
if(dp[head][tail]) return dp[head][tail];//!!
int r = INT_MIN;
for(int i=head; i<=tail; ++i)
r = max(r, ns[head-1]*ns[i]*ns[tail+1] + bb(ns,dp,head,i-1)+bb(ns,dp,i+1,tail));
return dp[head][tail] = r;
}
};http://youngyf.github.io/2016/03/03/leetcode-312-Burst-Balloons/
25.15 256. Paint House
 https://leetcode.com/problems/paint-house/
https://leetcode.com/problems/paint-house/
There are a row of n houses, each house can be painted with one of the three colors: red, blue or green. The cost of painting each house with a certain color is different. You have to paint all the houses such that no two adjacent houses have the same color.
The cost of painting each house with a certain color is represented by a n x 3 cost matrix. For example, costs[0][0] is the cost of painting house 0 with color red; costs[1][2] is the cost of painting house 1 with color green, and so on… Find the minimum cost to paint all houses.
Note: All costs are positive integers.
https://segmentfault.com/a/1190000003903965
复杂度
时间 \(O(N*3)\) 空间 \(O(N*3)\)
思路
直到房子i,其最小的涂色开销是直到房子i-1的最小涂色开销,加上房子i本身的涂色开销.但是房子i的涂色方式需要根据房子i-1的涂色方式来确定,所以我们对房子i-1要记录涂三种颜色分别不同的开销,这样房子i在涂色的时候,我们就知道三种颜色各自的最小开销是多少了.
我们在原数组上修改,可以做到不用extra空间.
struct Solution {
int minCost(vector<vector<int>>& costs) {
if (costs.empty()) return 0;
int L = costs.size();
for(int i=1; i<L; ++i){
// 涂第一种颜色的话,上一个房子就不能涂第一种颜色
// 这样我们要在上一个房子的第二和第三个颜色的最小
// 开销的两个方案中找最小的那个加上
costs[i][0] += min(costs[i-1][1], costs[i-1][2]);
// 涂第二或者第三种color(ditto)
costs[i][1] += min(costs[i-1][0], costs[i-1][2]);
costs[i][2] += min(costs[i-1][0], costs[i-1][1]);
}
// 返回涂三种颜色中开销最小的那个
return min(min(costs[L-1][0],costs[L-1][1]),costs[L-1][2]);
}
};- JAVA
class Solution {
public int minCost(int[][] costs) {
if(costs==null || costs.length==0 || costs[0]==null) return 0;
int L=costs.length;
for(int i=1;i<L;++i){
costs[i][0]+=Math.min(costs[i-1][1],costs[i-1][2]);
costs[i][1]+=Math.min(costs[i-1][0],costs[i-1][2]);
costs[i][2]+=Math.min(costs[i-1][0],costs[i-1][1]);
}
return Math.min(Math.min(costs[L-1][0],costs[L-1][1]),costs[L-1][2]);
}
}In Java, we can use x.length to get array’s size.
假设用红蓝绿三种颜色来凃房子.cumulative costs矩阵M是我们最终要生成的矩阵.M[i][0]的含义是假设在第i个房子凃红色,最小的花销是多少.M[i][1], M[i][2]的含义以此类推.
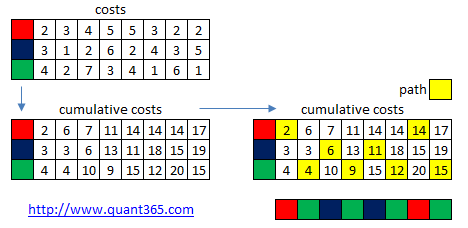
如上图,有了这个cumulative costs matrix之后我们可以反推出最优路径.注意一定是反推.在上面的例子中,从最后的一列出发.最小的是15,在绿色那行,然后之前一列非绿色的最小行是红,再之前非红的最小是绿,这样一直推到头就是最优路径.
struct Solution {
int minCost(vector<vector<int>>& costs) {
if(costs.empty() || costs[0].empty()) return 0;
int L=costs.size();
for(int i=1; i<L; ++i){
costs[i][0] += min(costs[i-1][1], costs[i-1][2]);
costs[i][1] += min(costs[i-1][0], costs[i-1][2]);
costs[i][2] += min(costs[i-1][0], costs[i-1][1]);
}
// 下面的代码是为了求出路径
vector<int> path(L);
auto& t=costs.back();
if(t[0]<t[1] && t[0]<t[2]) path[L-1]=0;
else if(t[1]<t[0] && t[1]<t[2]) path[L-1]=1;
else path[L-1]=2;
for(int i=L-2;i>=0;i--){
int mi=INT_MAX;
for(int j=0;j<3;j++){
if(j!=path[i+1])
if(mi>costs[i][j]) path[i]=j, mi=costs[i][j];
}
}
//for(auto i: path) cout << i << endl; // 打印出路径
return min(min(costs[L-1][0],costs[L-1][1]),costs[L-1][2]);
}
};测试上面程序通过.
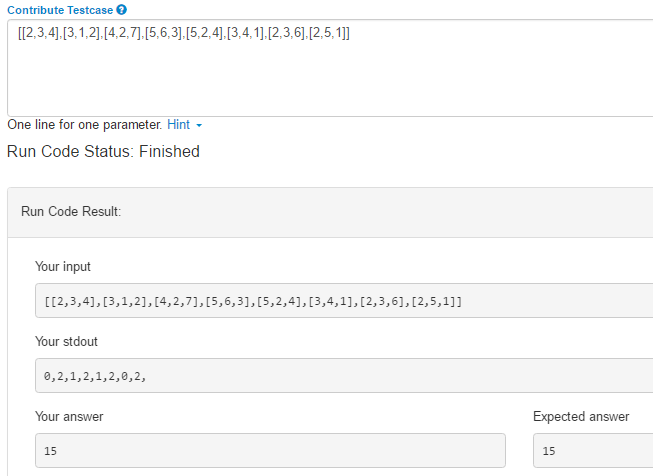
25.16 265. Paint House II
 https://leetcode.com/problems/paint-house-ii/
https://leetcode.com/problems/paint-house-ii/
There are a row of n houses, each house can be painted with one of the k colors. The cost of painting each house with a certain color is different. You have to paint all the houses such that no two adjacent houses have the same color.
The cost of painting each house with a certain color is represented by a n x k cost matrix. For example, costs[0][0] is the cost of painting house 0 with color 0; costs[1][2] is the cost of painting house 1 with color 2, and so on… Find the minimum cost to paint all houses.
Note: All costs are positive integers.
Follow up: Could you solve it in O(nk) runtime?
复杂度
时间 \(O(NK)\) 空间 \(O(1)\)
思路
和I的思路一样,不过这里我们有K个颜色,不能简单的用min方法了.如果遍历一遍颜色数组就找出除了自身外最小的颜色呢?我们只要把最小和次小的都记录下来就行了,这样如果和最小的是一个颜色,就加上次小的开销,反之,则加上最小的开销.
struct Solution {
int minCostII(vector<vector<int>>& costs) {
if(costs.empty()) return 0;
int ROW = costs.size(), COL= costs[0].size();
for(int i=1; i<ROW; i++){
// 如何找数列的最小和次小元素.
// Find the 1st and 2nd smallest cell in previous costs.
pair<int,int> prev_min(-1, INT_MAX), prev_sec(-1,INT_MAX);
for(int j=0; j<COL; j++){
if (costs[i-1][j] < prev_min.second)
prev_sec = prev_min, prev_min = {j, costs[i-1][j]};
else if(costs[i-1][j] < prev_sec.second)
prev_sec = {j, costs[i-1][j]};
}
for(int j=0; j<COL; j++)
costs[i][j] += (prev_min.first==j)?prev_sec.second:prev_min.second;
}
int r=INT_MAX;
for(int j=0; j<COL; j++) r = min(r,costs[ROW-1][j]);
return r;
}
};25.17 198. House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
 https://leetcode.com/problems/house-robber/
https://leetcode.com/problems/house-robber/
假设N的时候问题已经解决,现在考虑加一个数在末尾如何求N+1的情况.
根据是否最后一个房子被rob了有两种情况.

- 如何做这种题?
永远i是长度, 首先得出f(i+1)=max(f(i), f(i-1)+A’[i+1]), 这里的A’[i]是以1-based的一种表达方式. 然后上面的式子和下面这个在数学上等价: f(i)=max(f(i-1),f(i-2)+A’[i], i is Length here, i>=2因为长度不可能为负.
i仍然表示长度,放在f(i)中没有问题,但是A’[i]这种表示在C++里面是不行的,因为C++规定了index是0为起始点的.所以我们在程序中必须把A’[i]改为A[i-1].
因为递推公式只是说了i>=2的情况, 我们必须检查i==1和i==0的情况. 我们知道:
f(1)=A[0]
f(2)=max(f[1],f[0]+A[1])=max(A[0],A[1])所以f[0]必然等于0. 所以代码如下:
struct Solution { // T:O(N), S:O(N), two seed values
int rob(vector<int>& nums) {
if(nums.empty()) return 0;
vector<int> dp(nums.size()+1);
dp[0]=0, dp[1]=nums[0];
for(int i=2;i<=nums.size();++i)
dp[i]=max(dp[i-1],dp[i-2]+nums[i-1]);
return dp.back();
}
};还有其他写法比如i是0-based index, f(i)=max(f(i-1),f(i-2)+A’[i] this is still true, but now i is index, so A’[i]=A[i]. So we can use this formula in code directly. BUT there is some changes for the bootstrap values: f(0)=A[0], f(1)=max(A[0],A[1]). The forumla works from i=1 … So the code is like:
struct Solution { // T:O(N), S:O(N), two seed values
int rob(vector<int>& nums) {
if(nums.empty()) return 0;
vector<int> dp(nums.size());
dp[0]=nums[0];
for(int i=1;i<nums.size();++i)
dp[i]=max(dp[i-1],dp[i-2]+nums[i]);
return dp.back();
}
};可以用类似rolling array降维的思想把Space complexity降到O(1).
struct Solution { // T:O(N), S:O(1)
int rob(vector<int>& nums) {
if(nums.empty()) return 0;
int c, p, pp=nums[0];
if(nums.size()==1) return pp;
p=max(nums[0],nums[1]);
if(nums.size()==2) return p;
for(int i=2;i<nums.size();++i)
c=max(p,pp+nums[i]), pp=p, p=c;
return c;
}
};
25.18 213. House Robber II
Note: This is an extension of House Robber.
After robbing those houses on that street, the thief has found himself a new place for his thievery so that he will not get too much attention. This time, all houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, the security system for these houses remain the same as for those in the previous street.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
https://leetcode.com/problems/house-robber-ii
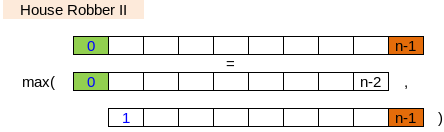

struct Solution {
int rob(vector<int>& nums) {
if(nums.empty()) return 0;
if(nums.size()==1) return nums[0];//edge case
return max(sub(nums,1,nums.size()-1),sub(nums,0,nums.size()-2));
}
int sub(vector<int>& nums,int h, int t){
int c=0, p=0, pp=0;
while(h<=t)
c=max(p,pp+nums[h]), pp=p, p=c, ++h;
return c;
}
};25.19 337. House Robber III
The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.
Determine the maximum amount of money the thief can rob tonight without alerting the police.
Example 1:
3
/ \
2 3
\ \
3 1Maximum amount of money the thief can rob = 3 + 3 + 1 = 7. Example 2:
3
/ \
4 5
/ \ \
1 3 1Maximum amount of money the thief can rob = 4 + 5 = 9.
https://leetcode.com/problems/house-robber-iii
分两种情况,抢root和不抢root.
struct Solution {
int rob(TreeNode* root) {
auto res = robHelper(root);
return max(res.first, res.second);
}
//return { max if rob root, max if not rob root}
pair<int, int> robHelper(TreeNode* root) {
if (!root) { return {0, 0}; }
auto left = robHelper(root->left);
auto right = robHelper(root->right);
return {root->val + left.second + right.second,
max(left.first, left.second) + max(right.first, right.second)};
}
};题目中给的例子看似好像是要每隔一个偷一次,但实际上不一定只隔一个,比如如下这个例子:4->1->2->3. 如果隔一个偷,那么是4+2=6,其实最优解应为4+3=7,隔了两个.
https://github.com/kamyu104/LeetCode/blob/master/C++/house-robber-iii.cpp
25.20 Delete and Earn
Given an array of n integers named elements, we can perform several steps on the array. In each step, we choose an elementsi from the array and delete it to earn elements i points; However, deleting elements i also deletes any integers equal to elements i + 1 and elements i - 1 from elements. For exampls, if elements = [1,2,3,4], deleting 2 results in elements becoming [4] and earns us 2 points.
Compute the maxPoints function that has one parameter; an array of n integers named elements. The function must return a long integer denoting the maximum number of points we can earn by performing steps.
Constraints
1<= n <= 10 (to the power 5)
1 <= elements i <= 10 (to the power 5)
Sample Input : [3,4,2]
Output : 6
Explanation:
Given elements = [3,4,2], we maximize our score by performing the following steps:
Delete 4 to earn 4 points, which also deletes 4 - 1 = 3 and elements becomes [2].
Delete 2 to earn 2 points and elements become
There are no more elements to delete, so we can’t perform any more steps. The function returns the total number of points which is 4 + 2 = 6.
- Algo:
First I come up with the idea that each time we delete the maximum value. But it obviously doesn’t work in this case: 1 1 1 2.
So I think about storing how many times a certain value occurs. Then each time we delete the element whose sum is the largest. But again it doesn’t work in this case: 1 1 1 2 2 3. The sum of 2 is 4. So we delete 2 first. We get only 4. But if we delete 1 and 3 first. We get 6.
Then the problem becomes pretty similar to https://leetcode.com/problems/house-robber/.
Say A[i] represents the sum of element i.
dp[i] = max(dp[i - 1], dp[i - 2] + A[i])Suppose the maximum of the elements is MAX. Then we can simply go from dp[0] to dp[MAX], which is O(n). dp[MAX] is our answer. Since MAX <= \(10^5\), we can do this. Otherwise we need to use unordered_map then sort the unordered_map. Or directly use map(I’m talking about C++). The time complexity of either of them will become O(nlogn).
25.21 Longest Common Subsequence
 http://www.lintcode.com/en/problem/longest-common-subsequence/
http://www.lintcode.com/en/problem/longest-common-subsequence/
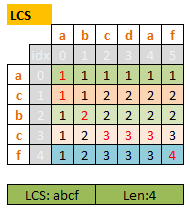
Recurrence equation is at CLRS P393.
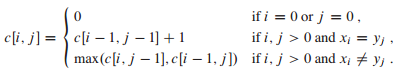
http://www.geeksforgeeks.org/dynamic-programming-set-4-longest-common-subsequence/
http://lcs-demo.sourceforge.net/
https://www.hackerrank.com/challenges/dynamic-programming-structics-the-longest-common-subsequence
- DP
struct Solution {
int longestCommonSubsequence(string A, string B) {
if(A.empty() || B.empty()) return 0;
return lcs(&A.front(), &B.front(), A.size(), B.size());
}
/*Following steps build L[m+1][n+1] in bottom up fashion. Note
that L[i][j] contains length of LCS of X[0..i-1] and Y[0..j-1] */
int lcs(char *X, char *Y, int m, int n){
int L[m+1][n+1], i, j;
for (i=0; i<=m; i++)
for (j=0; j<=n; j++){
if (i == 0 || j == 0) L[i][j] = 0;
else if (X[i-1] == Y[j-1])
L[i][j] = L[i-1][j-1] + 1;
else
L[i][j] = max(L[i-1][j], L[i][j-1]);
}
return L[m][n];
}
};- DFS + Memo
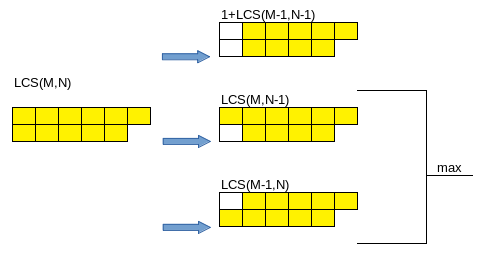
int lcs_rec(char *X, char *Y, int m, int n ) {
if (m == 0 || n == 0) return 0;
if (X[m-1] == Y[n-1]) return 1 + lcs(X, Y, m-1, n-1);
else return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));
}class Solution {
public:
map<int,map<int,int>> mm;
int longestCommonSubsequence(string A, string B) {
if(A.empty() or B.empty()) return 0;
return rec(A,A.size()-1,B,B.size()-1);
}
int rec(string a, int x, string b, int y){
if(x<0 or y<0) return 0;
if(mm.count(x) and mm[x].count(y)) return mm[x][y];
if(a[x]==b[y]) return mm[x][y]=1+rec(a,x-1,b,y-1);
return mm[x][y]=max(rec(a,x-1,b,y),rec(a,x,b,y-1));
}
};25.22 174. Dungeon Game
https://leetcode.com/problems/dungeon-game/
在走完最后一个房间的时候血量至少要剩下1,因此最后的状态可以当成是初始状态,由后往前依次决定在每一个位置至少要有多少血量, 这样一个位置的状态是由其下面一个和和左边一个的较小状态决定 .因此一个基本的状态方程是:
dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j].
但是还有一个条件就是在每一个状态必须血量都要大于1,因此我们还需要一个方程在保证在每一个状态都大于1,即:dp[i][j] = max(dp[i][j], 1); 也就是说虽然当前的血量到最后能够剩下1,但是现在已经低于1了,我们需要为其提升血量维持每一个状态至少都为1.
class Solution {
public:// dp[i][j] = max(min(dp[i+1][j]-B[i][j],dp[i][j+1]-B[i][j]),1)
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int m = dungeon.size(), n=dungeon[0].size();
vector<vector<int>> dp(m, vector<int>(n,INT_MAX));
dp[m-1][n-1] = max(1-dungeon[m-1][n-1],1);
for(int i = m-1; i>=0; i--){
for(int j =n-1; j>=0; j--){
if(i+1<m && j+1<n){
int val = min(dp[i+1][j], dp[i][j+1])-dungeon[i][j];
dp[i][j] = max(val, 1);
}else if(i+1<m){
dp[i][j] = max(dp[i+1][j]-dungeon[i][j],1);
}else if(j+1<n)
dp[i][j] = max(dp[i][j+1]-dungeon[i][j],1);
}
}
return dp[0][0];
}
};struct Solution {
int calculateMinimumHP(vector<vector<int>>& dungeon) {
int m = dungeon.size(), n=dungeon[0].size();
vector<vector<int>> dp(m+1, vector<int>(n+1,INT_MAX));
dp[m-1][n] = 1;
for(int i = m-1; i>=0; i--){
for(int j =n-1; j>=0; j--){
int val = min(dp[i+1][j], dp[i][j+1])-dungeon[i][j];
dp[i][j] = max(val, 1);
}
}
return dp[0][0];
}
}; 25.23 494. Target Sum
You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.
Find out how many ways to assign symbols to make sum of integers equal to target S.
Example 1:
Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3There are 5 ways to assign symbols to make the sum of nums be target 3.
Note:
- The length of the given array is positive and will not exceed 20.
- The sum of elements in the given array will not exceed 1000.
- Your output answer is guaranteed to be fitted in a 32-bit integer.
https://leetcode.com/problems/target-sum
class Solution {
map<pair<int,int>,int> d;
public:
int findTargetSumWays(vector<int>& nums, int S) { // d[{nums.size(), S}]??
return dp(nums, nums.size(), S);
}
int dp(vector<int>& nums, int sz, int t){
if(d.count({sz,t})) return d[{sz,t}];
if(sz==1) return int(nums[0]==t) + int(nums[0]==-t);
int k=dp(nums,sz-1,t-nums[sz-1])+dp(nums,sz-1,t+nums[sz-1]);
return d[{sz,t}]=k;
}
};一看这题可以用自顶向下的DP解决. 这其实是一个二维DP,但是不能用矩阵形式,因为矩阵的大小无从知道,而且不需要算矩阵里面的无用点. 所以用map形式.上面代码简洁明快.
注意如果key是pair的话不能用unordered_map,因为没有对应的hash function.但是可以用map, 对应是comparator是存在的.
25.24 85. Maximal Rectangle
Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 6.
https://leetcode.com/problems/maximal-rectangle
http://shibaili.blogspot.com/2014/12/day-83-85-maximal-rectangle.html
求高度要用DP.
25.25 221. Maximal Square
Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.
For example, given the following matrix:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Return 4.
https://leetcode.com/problems/maximal-square
https://leetcode.com/articles/maximal-square
这个题感觉很难想到.难度不小!
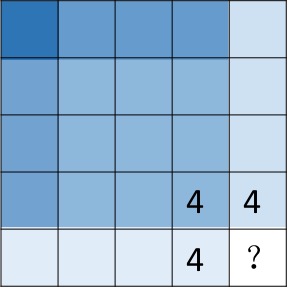
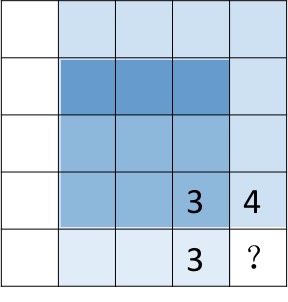
http://bgmeow.xyz/2017/01/10/LeetCode-221/
struct Solution {
int maximalSquare(vector<vector<char>>& m) {
int R=m.size(), C=0, mx=0;
if(R==0 || (C=m[0].size())==0) return 0; // 矩阵题模板开头
vector<vector<int>> r(R, vector<int>(C));
for(int i=0;i<R;++i)
for(int j=0;j<C;++j)
if(i==0 || j==0) r[i][j]=m[i][j]-'0', mx=max(mx,m[i][j]-'0');
else if(m[i][j]=='1')
r[i][j]=1+min(r[i-1][j-1],min(r[i-1][j],r[i][j-1])), mx=max(mx,r[i][j]);
return mx*mx;
}
};肯定可以用rolling array to optimize! 略.
25.26 650. 2 Keys Keyboard
Initially on a notepad only one character ‘A’ is present. You can perform two operations on this notepad for each step:
- Copy All: You can copy all the characters present on the notepad (partial copy is not allowed).
- Paste: You can paste the characters which are copied last time.
Given a number n. You have to get exactly n ‘A’ on the notepad by performing the minimum number of steps permitted. Output the minimum number of steps to get n ‘A’.
Example 1:
Input: 3
Output: 3
Explanation:
Intitally, we have one character 'A'.
In step 1, we use Copy All operation.
In step 2, we use Paste operation to get 'AA'.
In step 3, we use Paste operation to get 'AAA'.https://leetcode.com/problems/2-keys-keyboard
Contest的时候,这题一看就知道用bottom up的DP解决.
struct Solution {
int minSteps(int n) {
vector<int> dp(n+1);
dp[1]=0, dp[2]=2, dp[3]=3;
for(int i=4;i<=n;++i){
if(i%2==0) dp[i]=dp[i/2]+2;
else{
bool bb=0;
for(int k=i/3;k>=3;--k){
if(i%k==0){
dp[i]=dp[k]+i/k;
bb=1;
break;
}
}
if(bb==0) dp[i]=i;
}
}
return dp.back();
}
};后来看了人家的代码, 这个分析算是抓到了精髓:
/**
* It take 2 op to double, 3 ops to triple, ...
* if n % 2 == 0, then f(n) = f(n/2) + 2
* if n % 3 == 0, then f(n) = f(n/3) + 3
* 2 * 2 = 2 + 2, 2 * 3 > 2 + 3, 4 * 4 > 4 + 4, so it is always better to divide whenever possible.
* now it became a problem for finding all possible factors; */
struct Solution {
int minSteps(int n) {
if (n == 1) return 0;
for (int i = 2; i < n; i++)
if (n % i == 0) return i + minSteps(n / i);
return n;
}
};25.27 656. Coin Path
Given an array A (index starts at 1) consisting of N integers: A1, A2, …, AN and an integer B. The integer B denotes that from any place (suppose the index is i) in the array A, you can jump to any one of the place in the array A indexed i+1, i+2, …, i+B if this place can be jumped to. Also, if you step on the index i, you have to pay Ai coins. If Ai is -1, it means you can’t jump to the place indexed i in the array.
Now, you start from the place indexed 1 in the array A, and your aim is to reach the place indexed N using the minimum coins. You need to return the path of indexes (starting from 1 to N) in the array you should take to get to the place indexed N using minimum coins.
If there are multiple paths with the same cost, return the lexicographically smallest such path.
If it’s not possible to reach the place indexed N then you need to return an empty array.
Example 1:
Input: [1,2,4,-1,2], 2
Output: [1,3,5]
Example 2:
Input: [1,2,4,-1,2], 1
Output:
 https://leetcode.com/problems/coin-path
https://leetcode.com/problems/coin-path
这个题要求the lexicographically smallest such path,比如
25.27.1 Algo 1: DFS
一看求path,自然想到DFS. 代码如下:
struct Solution {
vector<int> cheapestJump(vector<int>& A, int B) {
if(A.empty() || !B) return {};
if(A.size()==1 && B>=1) return {1};
vector<vector<int>> r;
vector<int> p={1};
int gsum=INT_MAX;
for(int i=1; i<A.size()&&i<=B; ++i)
if(A[i]!=-1)
dfs(A, B, r, p, i, gsum, A[0]);
if(r.size()==1) return r.back();
if(r.empty()) return {};
sort(r.begin(), r.end(), [](const vector<int>& lhs, const vector<int>& rhs){
int M = lhs.size(), N = rhs.size();
for(int i = 0; i < min(M,N); i++)
if(lhs[i] != rhs[i]) return lhs[i] < rhs[i];
return M < N;
});
return r[0];
}
void dfs(vector<int>& a, int b, vector<vector<int>>& r, vector<int>& p,
int i, int& gsum, int csum)
{
if(gsum<csum) return;
if(i>=a.size()){
if(r.empty()){
r.push_back(p), gsum=csum;
}else{
if(gsum == csum){
if(r.back()!=p)r.push_back(p);
}else if(gsum > csum){
r.clear(), r.push_back(p), gsum=csum;
}
}
return;
}
for(int j=i; j<a.size() && j<i+b; j++){
if(a[j]==-1) continue;
if(!p.empty() && p.back()+b<j) continue; //
p.push_back(j+1);
dfs(a,b,r,p,j+1,gsum,csum+a[j]);
p.pop_back();
}
}
};这个复杂度太高TLE.
25.27.2 Algo 2: DP
一般的说法是DP不适合求路径. 这道题演示了如何用DP求最优路径. 比一般的DP复杂的是要track两个变量,一个是min cost,一个是路径. 而且这个路径还是一个vector.
bool operator<(const vector<int>& l, const vector<int>& r){
int m=l.size(), n=r.size();
for(int i=0;i<min(m,n);++i)
if(l[i]!=r[i]) return l[i]<r[i];
return m<n;
}
struct Solution {
vector<int> cheapestJump(vector<int>& A, int B) {
int L=A.size();
vector<int> dp(L+1, INT_MAX); // min cost
vector<vector<int>> pa(L+1, vector<int>()); // path
dp[1]=A[0], pa[1]={1}; // dp[x] min cost from 1 to x, pa[x] - path from 1 to x
for (int i=2; i<L+1; ++i) {
if (A[i-1]==-1) continue; // condition 1
for (int j=1; j<=B; j++) {
if (i-j<=0 || dp[i-j]==INT_MAX) continue; // condition 2
int t = dp[i-j] + A[i-1];
if(dp[i] > t){
dp[i] = dp[i-j] + A[i-1];
pa[i] = pa[i-j], pa[i].push_back(i);
}else if(dp[i] == t){
auto tp = pa[i-j];
tp.push_back(i);
if(tp < pa[i]){ pa[i]=tp;}
}
}
}
return pa[L];
}
};这道题还演示了如何重载运算符. dp[x]中的x表示长度. dp[1]和pa[1]都是反推出来的.
下面的方法采用backward moving,可以直接得到the lexicographically smallest path.
https://discuss.leetcode.com/topic/98399/c-dp-o-nb-time-o-n-space
struct Solution {
vector<int> cheapestJump(vector<int>& A, int B) {
vector<int> ans;
if (A.empty() || A.back() == -1) return ans;
int n = A.size(), k = 0;
vector<int> dp(n, INT_MAX), po(n,-1);
dp[n-1] = A[n-1];
for (int i = n-2; i >= 0; i--) { // working backward
if (A[i] == -1) continue;
for (int j = i+1; j <= min(i+B, n-1); j++) {
if (dp[j] == INT_MAX) continue;
if (A[i]+dp[j] < dp[i])
dp[i] = A[i]+dp[j], po[i] = j;
}
}
if (dp[0] == INT_MAX) return ans; // cannot jump to An
while (k!=-1)
ans.push_back(k+1), k = po[k];
return ans;
}
};Similar Problem: Jump Game II
25.28 279. Perfect Squares
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
For example, given n = 12, return 3 because 12 = 4 + 4 + 4; given n = 13, return 2 because 13 = 4 + 9.
https://leetcode.com/problems/perfect-squares
25.28.1 Algo 1: Naive DP
This naive DP will cause stack overflow.
class Solution {
public:
int numSquares(int n) {
static vector<int> dp(n+1,-1);
if(dp[n]!=-1) return dp[n];
if(isps(n)) return dp[n]=1;
int r=INT_MAX;
for(int i=1;i<n;++i)
if(isps(i))
dp[i]=1, r=min(r, 1+numSquares(n-i));
return dp[n]=(r==INT_MAX?1:r);
}
bool isps(int x){ // is perfect square
static vector<short> ps(x+1,-1);
if(ps[x]!=-1) return ps[x];
int h=1, t=(x+1)/2;
while(h<=t){
long long m=h+(t-h)/2, p=m*m;
if(p>x) t=m-1;
else if(p<x) h=m+1;
else return ps[x]=1;
}
return ps[x]=0;
}
};Actually we don’t have to check if a number is square.
25.28.3 Algo 3: Lagrange Four-square Theorem
先来看第一种很高效的方法,根据四平方和定理,任意一个正整数均可表示为4个整数的平方和,其实是可以表示为4个以内的平方数之和,那么就是说返回结果只有1,2,3或4其中的一个,首先我们将数字化简一下,由于一个数如果含有因子4,那么我们可以把4都去掉,并不影响结果,比如2和8,3和12等等,返回的结果都相同,读者可自行举更多的栗子.还有一个可以化简的地方就是,如果一个数除以8余7的话,那么肯定是由4个完全平方数组成,这里就不证明了,因为我也不会证明,读者可自行举例验证.那么做完两步后,一个很大的数有可能就会变得很小了,大大减少了运算时间,下面我们就来尝试的将其拆为两个平方数之和,如果拆成功了那么就会返回1或2,因为其中一个平方数可能为0. (注:由于输入的n是正整数,所以不存在两个平方数均为0的情况).注意下面的!!a + !!b这个表达式,可能很多人不太理解这个的意思,其实很简单,感叹号!表示逻辑取反,那么一个正整数逻辑取反为0,再取反为1,所以用两个感叹号!!的作用就是看a和b是否为正整数,都为正整数的话返回2,只有一个是正整数的话返回1,参见代码如下:
25.29 664. Strange Printer
There is a strange printer with the following two special requirements:
- The printer can only print a sequence of the same character each time.
- At each turn, the printer can print new characters starting from and ending at any places, and will cover the original existing characters.
Given a string consists of lower English letters only, your job is to count the minimum number of turns the printer needed in order to print it.
Example 1:
Input: “aaabbb”
Output: 2
Explanation: Print “aaa” first and then print “bbb”.
Example 2:
Input: “aba”
Output: 2
Explanation: Print “aaa” first and then print “b” from the second place of the string, which will cover the existing character ‘a’.
Hint: Length of the given string will not exceed 100.
https://leetcode.com/problems/strange-printer
25.29.1 Algo: 2D DP 3loops
假设已知字符串为’abcd’, r=4. 如果后面分别加a,b,c,d结果应该都是4; 如果加e结果是5.
struct Solution {
int strangePrinter(string s) {
int L = s.length();
if (L == 0) return 0;
vector<vector<int>> dp(L,vector<int>(L));
for (int i = 0; i < L; i++) dp[i][i] = 1;
for (int len = 1; len < L; len++) {
for (int j = 0; j < L - len; j++) {
dp[j][j+len] = len + 1; //
for (int k = j+1; k <= j+len; k++) {
int temp = dp[j][k-1] + dp[k][j+len];
if (s[k-1] == s[j+len]) temp--; // a|bcda, ba|cda, bcda|a
dp[j][j + len] = min(dp[j][j + len], temp);
}
}
}
return dp[0][L - 1];
}
};for (int i = 0; i < L; i++) dp[i][i] = 1;
for (int len = 1; len < L; len++) {
for (int j = 0; j < L - len; j++) {
dp[j][j+len] = len + 1;
//...
}
}25.30 418. Sentence Screen Fitting
Given a rows x cols screen and a sentence represented by a list of non-empty words, find how many times the given sentence can be fitted on the screen.
Note: A word cannot be split into two lines. No empty word. The order of words in the sentence must remain unchanged. Two consecutive words in a line must be separated by a single space.
Example 1:
Input: rows = 3, cols = 6, sentence = [“a”, “bcd”, “e”]
Output: 2
Explanation:
a-bcd-
e-a---
bcd-e-Example 2:
Input: rows = 4, cols = 5, sentence = [“I”, “had”, “apple”, “pie”]
Output: 1
Explanation:
I-had
apple
pie-I
had--The character ‘-’ signifies an empty space on the screen.
https://leetcode.com/problems/sentence-screen-fitting
25.30.1 Algo 1: Greedy - Brute Force
用Brute Force算法能算出结果,但是会超时(eg. input: [“a”], 20000, 20000).
struct Solution {
int wordsTyping(vector<string>& s, int ro, int co) {
int r=0, i=0, j=0, L=s.size(), k=0;
while(i<=ro*co){
while(i<=ro*co && j<L){
int x=i+s[j].size()+(i%co!=0), y=(k+1)*co;
if(x <= y){
i=x, j++;
}else{
i=y, k++;
}
}
if(i >ro*co) return r;
if(i==ro*co) return r+(j==L);
if(j==L)
r++, j=0;
}
return r;
}
};25.30.2 Algo 2: Memoization
https://en.wikipedia.org/wiki/Memoization
Take input ([“a”, “bcd”, “e”], 3, 6) as an example, it is easy to see how to optimize the solution. If we track the number of words in one line starting with a specific word, then we can reuse the information later.
int wordsTyping(vector<string>& sentence, int rows, int cols) {
unordered_map<int, int> umap;
int num = 0, n = sentence.size();
for(int i = 0; i < rows; i++){
int start = num % n;
if(umap.count(start) == 0){
int cnt = 0, len = 0;
for(int i = start; len < cols; i = (i+1) % n, cnt++){
if(len + sentence[i].size() > cols)
break;
len += sentence[i].size() + 1;
}
num += cnt;
umap.emplace(start, cnt);
}
else
num += umap[start];
}
return num / n;
}Here num is the total number of words which can be put into the area.
25.31 70. Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
- 1 step + 1 step + 1 step
- 1 step + 2 steps
- 2 steps + 1 step