Chapter 14 Binary Tree
Tree <=> Graph which is connected and no cycle(acyclic) and directed.
14.1 Basics of Tree Depth, Height and Level
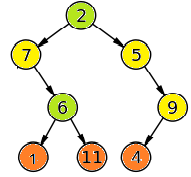
节点分为5类: empty node, leaf node, half node(left missing, right missing), full/inner node.
- Given a binary tree, how do you remove all the half nodes?
http://www.geeksforgeeks.org/given-a-binary-tree-how-do-you-remove-all-the-half-nodes/
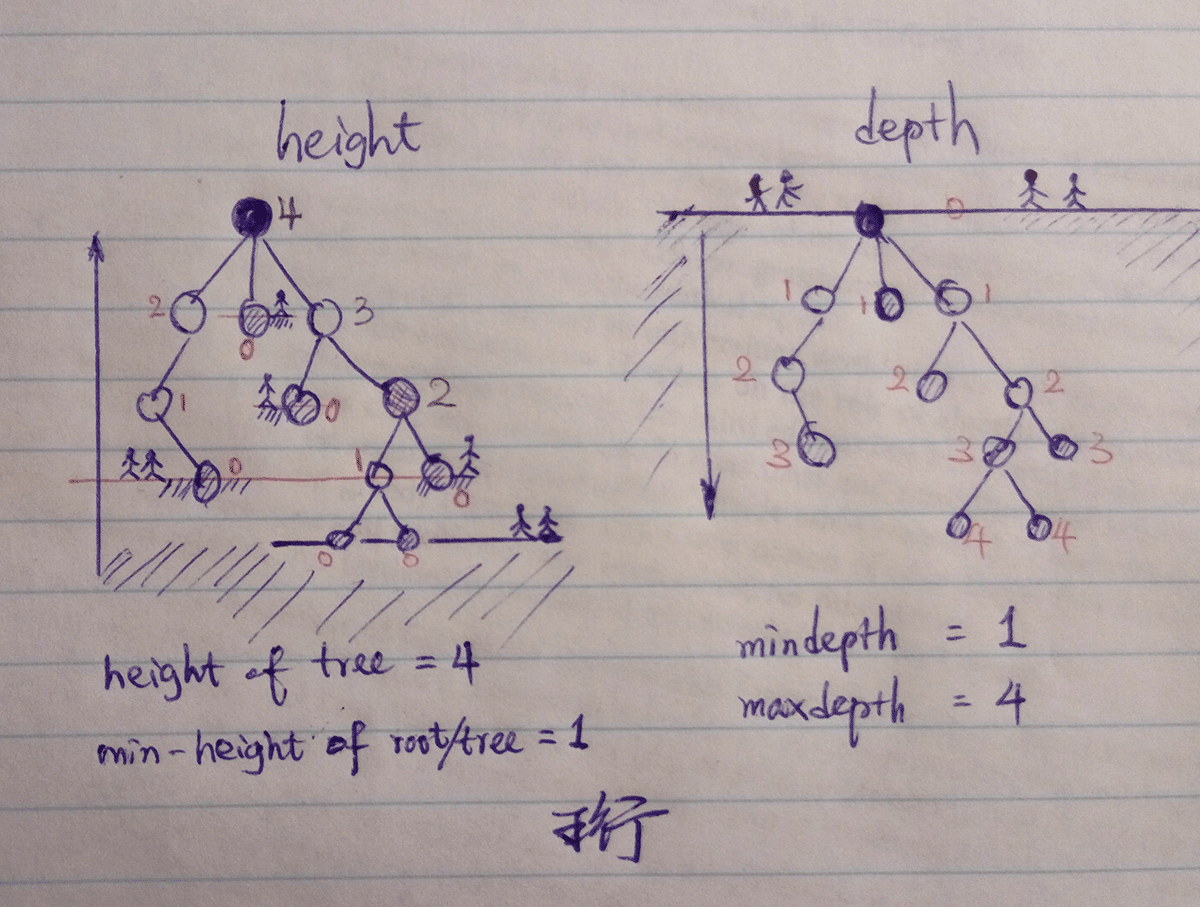
根据CLRS的定义,一个点的高度height是该点到叶节点的Edge(边)的个数,深度depth是根节点到该点之间的edge的个数.
其实这些定义都是很灵活的,便于人们交流而已. Leetcode的题目种就不是这样定义的, Leetcode是看Node的个数(包括自身).
14.2 222. Count Complete Tree Nodes
Given a complete binary tree, count the number of nodes.
https://leetcode.com/problems/count-complete-tree-nodes/
class Solution {
public int countNodes(TreeNode root) {
if(root==null) return 0;
int l=height(root.left, true);
int r=height(root.right, false);
if(l==r) return (1<<l)-1; // perfect tree
return countNodes(root.left)+countNodes(root.right)+1;
}
private int height(TreeNode r, boolean left){
if(r==null) return 1; // not 0
int c=1; //
while(r!=null){
r=left?r.left:r.right;
c++;
}
return c;
}
}We know perfect tree’s node number can be calculated with a math formula.
14.3 606. Construct String from Binary Tree
You need to construct a string consists of parenthesis and integers from a binary tree with the preorder traversing way. The null node needs to be represented by empty parenthesis pair “()”. And you need to omit all the empty parenthesis pairs that don’t affect the one-to-one mapping relationship between the string and the original binary tree.
Example 1:
Input: Binary tree: [1,2,3,4]
1
/ \
2 3
/
4
Output: "1(2(4))(3)"Explanation: Originallay it needs to be “1(2(4)())(3()())”, but you need to omit all the unnecessary empty parenthesis pairs. And it will be “1(2(4))(3)”.
Example 2:
Input: Binary tree: [1,2,3,null,4]
1
/ \
2 3
\
4
Output: "1(2()(4))(3)"Explanation: Almost the same as the first example, except we can’t omit the first parenthesis pair to break the one-to-one mapping relationship between the input and the output.
https://leetcode.com/problems/construct-string-from-binary-tree
class Solution {
public:
string tree2str(TreeNode* t) {
if(!t) return "";
string r=to_string(t->val);
if(t->left || t->right) // non leaf node
r+='('+tree2str(t->left)+')';
if(t->right)
r+='('+tree2str(t->right)+')';
return r;
}
};如果不要求节约那个(),程序应该这样写:
struct Solution {
string tree2str(TreeNode* t) {
if(!t) return "";
if(!t->left && !t->right) // leaf node
return to_string(t->val);
string r=to_string(t->val);
r+='('+tree2str(t->left)+')';
r+='('+tree2str(t->right)+')';
return r;
}
};如果要求节约右边的(),加一个条件就行了:
14.4 22. Generate Parentheses
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]https://leetcode.com/problems/generate-parentheses/
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> r;
string s;
dfs(r,s,0,n);
return r;
}
// l is how many left is greater than right; n is matching number
void dfs(vector<string>& vs, string s, int l, int n){
if(l==0){
if(n==0){vs.push_back(s); return;} // base condition 1
dfs(vs,s+'(',1,n);
}else{
if(l>n or n==0) return; //base condition 2
dfs(vs,s+")",l-1,n-1);
dfs(vs,s+"(",l+1,n);
}
}
};- Java
class Solution {
public List<String> generateParenthesis(int n) {
List<String> r=new ArrayList<>();
String s="";
dfs(r, s, 0, n);
return r;
}
void dfs(List<String> r, String s, int l, int n){
if(l==0){
if(n==0){ r.add(s); }else{
dfs(r,s+'(',l+1, n);// n - not matched by ); l - extra l
}
}else{
if(l>n || n==0) return;
dfs(r,s+")",l-1,n-1);
dfs(r,s+'(',l+1,n);
}
}
}14.5 Graph Valid Tree
https://www.lintcode.com/en/problem/graph-valid-tree/
http://www.cnblogs.com/grandyang/p/5257919.html
DFS
BFS
Union Find
See here: array or graph-valid-tree
14.6 Number Tree - LeetCode 386. Lexicographical Numbers
https://leetcode.com/problems/lexicographical-numbers/
Given an integer n, return 1 – n in lexicographical order.
For example, given 13, return: [1,10,11,12,13,2,3,4,5,6,7,8,9].
Please optimize your algorithm to use less time and space. The input size may be as large as 5,000,000.
- Algo 1: DFS
The result sequence is a DFS sequence on this denary(10-ary) number tree.
(This is not a trie.)
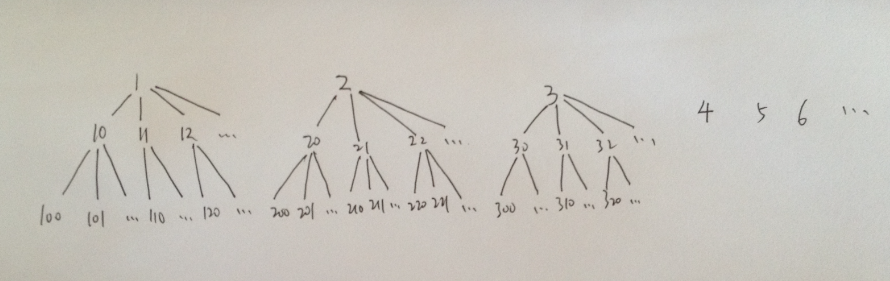
struct Solution {
vector<int> lexicalOrder(int n) {
vector<int> r;
for(int i=1;i<10;++i)
dfs_10ary_tree(r, n, i); // n=13
return r;
}
void dfs_10ary_tree(vector<int>& r, int n, int cur){
if(cur>n) return;
r.push_back(cur);
for(int i=0;i<10;++i)
dfs_10ary_tree(r, n, cur*10+i);
}
};Similar:
https://www.nayuki.io/page/next-lexicographical-permutation-algorithm
- Algo 2: Navigate in Number Tree
http://blog.csdn.net/niuooniuoo/article/details/52330444
public struct Solution {
public List<Integer> lexicalOrder(int n) {
List<Integer> list = new ArrayList<>(n);
int curr = 1;
for (int i = 1; i <= n; i++) {
list.add(curr);
if (curr * 10 <= n) {
curr *= 10; // visit下一层left most node
} else if (curr % 10 != 9 && curr + 1 <= n) {
curr++; // 同层移动
} else {
while ((curr/10) % 10 == 9)
curr /= 10;//个位是9的话,回溯,因为k+1又是10的倍数
curr = curr / 10 + 1;//回溯计算
}
}
return list;
}
}14.7 440. K-th Smallest in Lexicographical Order
Given integers n and k, find the lexicographically k-th smallest integer in the range from 1 to n.
Note: 1 <= k <= n <= 109.
Example:
Input: n: 13 k: 2
Output: 10
Explanation:
The lexicographical order is [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9], so the second smallest number is 10.
https://leetcode.com/problems/k-th-smallest-in-lexicographical-order
http://massivealgorithms.blogspot.com/2016/10/leetcode-440-k-th-smallest-in.html
calsteps function: how to calculate the steps between curr and curr + 1?
Here we come up an idea to calculate by level.
Let head = curr, tail = curr + 1.
tail is always the next right node beside head's right most node (who shares the same ancestor "curr")
(2 is right next to 1, 20 is right next to 19, 200 is right next to 199).
so, if tail <= n, which means head’s right most node exists, we can simply add the number of nodes from head to tail to steps.
else if tail > n, which means n(the boundary node) is on the path between head to tail, add (n + 1 - head) to steps.
struct Solution {
int findKthNumber(int n, int k) {
int cur = 1;
--k;
while (k) {
int steps = calsteps(n, cur);
if (steps <= k)
++cur, k -= steps;
else
cur *= 10, --k;
}
return cur;
}
// 在boundary condition n的情况下,找head到head+1之间的距离
int calsteps(long n, long head) {////
int steps = 0;
long tail = head + 1;
while (head <= n) {
if (tail <= n)
steps += tail - head;
else
steps += n - head + 1;
head *= 10, tail *= 10;
}
return steps;
}
};14.8 111. Minimum Depth of Binary Tree
Given a binary tree, find its minimum depth. The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
https://leetcode.com/problems/minimum-depth-of-binary-tree/
- BFS
BFS has a built-in feature, which is to find the shortest path. This makes BFS the best algorithm for this problem.
#define ISLEAF(n) (n->left==NULL && n->right==NULL)
int minDepth(TreeNode* root) {
if (!root) return 0;
int r = 1;
queue<TreeNode*> Q;
Q.push(root), Q.push(0); // push an extra dummy node
while (!Q.empty()) {
TreeNode* n = Q.front(); Q.pop();
if (n == 0)
r++, Q.push(0); //dummy node to mark a new layer
else {
if (ISLEAF(n)) return r;
if (n->left) Q.push(n->left);
if (n->right) Q.push(n->right);
}
}
return 0;//placeholder
}- DFS
We can still use DFS but we have to full-scan the tree and use function \(min(\cdot)\) to find the mindepth.
Note: the base case in \(dfs(\cdot)\) is \(leaf node\).
int minDepth(TreeNode* root) {
if (!root) return 0;
int r = INT_MAX;
dfs(root, 1, r);
return r;
}
void dfs(TreeNode* root, int c, int& r) {// what is a leaf node?
if (!root->left and !root->right) { r = min(r, c); return; }
if (root->left) dfs(root->left, c + 1, r);
if (root->right) dfs(root->right, c + 1, r);
}- Recursion
int minDepth(TreeNode* root) {
if(!root) return 0; // empty node
if(!root->left and !root->right) return 1; // leaf node
if(!root->left) return minDepth(root->right)+1; // right half node
if(!root->right) return minDepth(root->left)+1; // left half node
return min(minDepth(root->left), minDepth(root->right))+1; // inner node
}14.9 104. Maximum Depth of Binary Tree
https://leetcode.com/problems/maximum-depth-of-binary-tree/
- Recursion
int maxDepth(TreeNode* root) {
return root ? max(maxDepth(root->left), maxDepth(root->right)) + 1 : 0;
}- DFS
14.10 366. Find Leaves of Binary Tree
Given a binary tree, collect a tree’s nodes as if you were doing this: Collect and remove all leaves, repeat until the tree is empty.
Example: Given binary tree
1
/ \
2 3
/ \
4 5 Returns [4, 5, 3], [2], [1].
Explanation:
1. Removing the leaves [4, 5, 3] would result in this tree:
1
/
2 - Now removing the leaf
[2]would result in this tree:
1 - Now removing the leaf
[1]would result in the empty tree:
[] Returns [4, 5, 3], [2], [1].
https://leetcode.com/problems/find-leaves-of-binary-tree/
http://www.cnblogs.com/grandyang/p/5616158.html
这个题本质是求每个节点的max height. 很有代表性: 节点的高度height是在递归函数rec回溯的时候确定!!!
节点在vector的index就等于节点的max height.
int dep = max(rec(r,n->left), rec(r,n->right)) + 1;很关键.
struct Solution {
vector<vector<int>> findLeaves(TreeNode* root) {
vector<vector<int>> r;
rec(r, root);
return r;
}
int rec(vector<vector<int>>& r, TreeNode* n){ // return depth
if(n==0) return -1; //注意返回值
int dep = max(rec(r,n->left), rec(r,n->right)) + 1;
if(r.size()<dep+1) r.resize(dep+1);
r[dep].push_back(n->val);
return dep;
}
};这里不是用的DFS,是递归.
上面那个rec返回的是CLRS定义的高度height(叶子节点高度为0). 其实这样也行,不过返回的是高度+1:
14.11 364. Nested List Weight Sum II
https://leetcode.com/problems/nested-list-weight-sum-ii/
这个题给上面那道相似但不同.
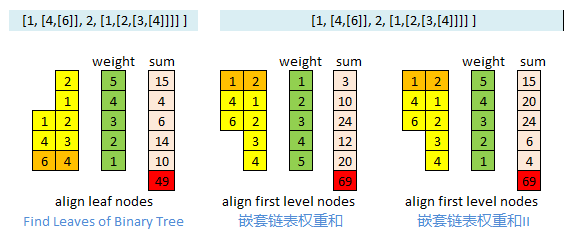
节点的深度depth是在DFS前进的时候确定!!!所以这个难度要小点.可以直接把depth作为一个参数传到\(dfs()\).
struct Solution {
int depthSumInverse(vector<NestedInteger>& nestedList) {
vector<int> r;
for(auto ni: nestedList) dfs(r, ni, 0);
int ans=0;
for(int i=r.size()-1, j=1; i>=0; --i) ans += (j++)*r[i];
return ans;
}
void dfs(vector<int>& r, NestedInteger n, int dep){
if(dep>=r.size()) r.resize(dep+1); // list也要占空间 [1,[2]] == 4
if(n.isInteger()){
r[dep] += n.getInteger();
}else
for(auto e : n.getList()) dfs(r, e, dep+1);
}
};NestedInteger是一个特别的int,可以是int,也可以是一个int的数组.
这道题的深度depth其实和上图的高度height相近但是又不完全相同.如果从树的角度来看,好比以最深那点为基准,所以没有任何冲突.不像树height的传统定义,没有固定的基准,任何叶子节点都可能是基准,这样会有冲突,造成max height或者min height的不同.
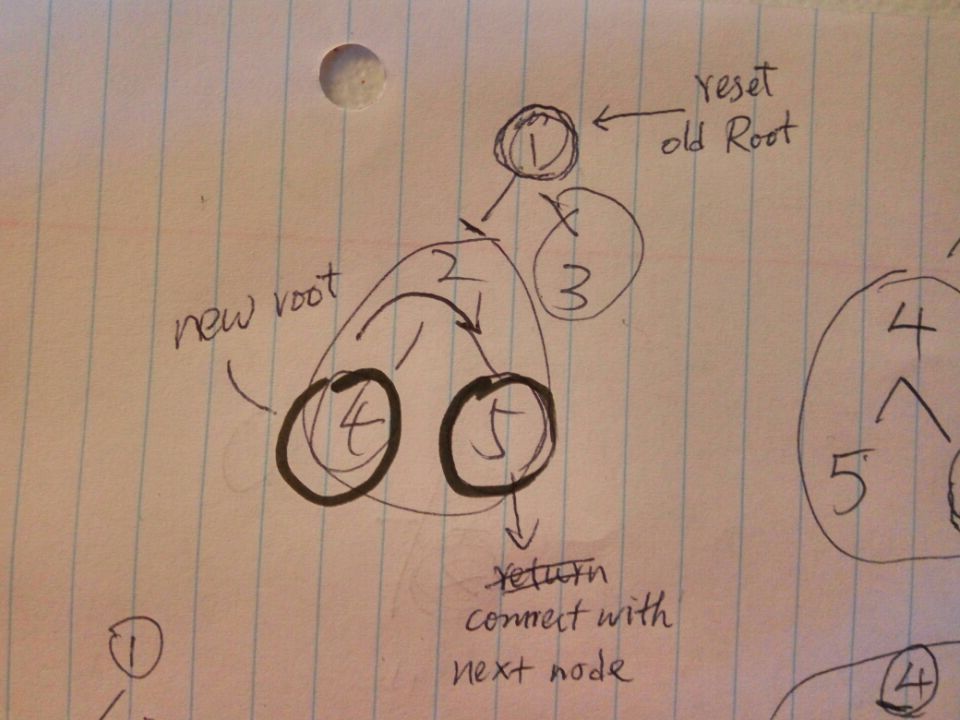
14.12 Binary Tree Upside Down
https://leetcode.com/problems/binary-tree-upside-down/
这题有一个重要的限制就是,整个数的任何一个右孩子都不会再生枝节,基本就是一个梳子的形状.
struct Solution {
TreeNode* upsideDownBinaryTree(TreeNode* R) {
if (!R) return R;
TreeNode *nR = R, *tmp = 0;
if (R->left){
nR = tmp = upsideDownBinaryTree(R->left); //chain assignment
while(tmp->right){tmp = tmp->right;}// can be optimized
tmp->left = R->right;
tmp->right = R, R->left = 0, R->right = 0;////!!!!
}
return nR;
}
};Right child node is a leaf or NULL, so it is not a problem. The crux is the left child node. We can imagine it as a subtree. We will return the root of the subtree as new root, and we also need the right most child as a connecting point to the original root(R) and original right child(R->right).
The tree is like a binary family tree, where left child is older brother and right child is younger brother. Whenever there is a younger brother, there must be a older brother. (You can definitely replace brother with sister.)
这题迭代的解法:
14.13 Flatten Binary Tree to Linked List
Given a binary tree, flatten it to a linked list in-place.
For example, Given
1
/ \
2 5
/ \ \
3 4 6The flattened tree should look like:
1
\
2
\
3
\
4
\
5
\
6https://leetcode.com/problems/flatten-binary-tree-to-linked-list/
struct Solution {
void flatten(TreeNode* root) { rec(root); }
TreeNode* rec(TreeNode* root){
if(!root) return root;
auto l = rec(root->left);
auto r = rec(root->right);
root->left = 0;
if(l){
root->right = l;
while(l->right) l=l->right; // rightmost
l->right = r;
}else{
root->right = r;
}
return root;
}
};两道leetcode原题
1. 判断一个array of integer是不是单调
2. flatten bst成为linkedlist,要求最后的linkedlist必须是sorted而且不能占用额外的空间.
14.14 Symmetric Tree
https://leetcode.com/problems/symmetric-tree/
下面这个是我自己写的代码.先找思路,首先iterative很难做,因为是按照对称路径在比较. 考虑recursive的方法.这个镜像树是只关于Root对称,不是任意节点对称.所以recursive function要接受两个参数.
struct Solution {
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return ismirror(root->left, root->right);
}
bool ismirror(TreeNode* l, TreeNode* r){
if(!l && !r) return true;
if((!l&&r) || (l&&!r) || l->val!=r->val) return false;
return ismirror(l->left, r->right) && ismirror(l->right, r->left);
}
};对root判断的logic其实可以包含在下面的recursive function里面,所以可以把代码稍微改短一行
1
/ \
2 2
/ \ / \
3 4 4 3
|
V
1 1
/ \
2 2
/ \ / \
3 4 4 3struct Solution {
bool isSymmetric(TreeNode* root) {
return ismirror(root, root);
}
bool ismirror(TreeNode* l, TreeNode* r){
if (not l and not r) return true;
if ((not l and r) or (not r and l) or (l->val != r->val)) return false;
return ismirror(l->left, r->right) and ismirror(l->right, r->left);
}
};方法就是: 左左右右….左孩子往左边走,右孩子往右边走….
14.15 Binary Tree Zigzag Level Order Traversal(BFS)
https://leetcode.com/problems/binary-tree-zigzag-level-order-traversal/
- Algo 1: Two stacks
A trap here is donot forget switching the order of pushing left and right child!!!
struct Solution {
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> r;
if (not root) return r;
stack<TreeNode*> Q1, Q2; ////
Q1.push(root);
r.push_back(vector<int>());
bool zz=true; // zigzag switch
while (!Q1.empty() || !Q2.empty()) {
stack<TreeNode*>* p1 = Q1.empty()?&Q2:&Q1;
stack<TreeNode*>* p2 = Q1.empty()?&Q1:&Q2;
while(!p1->empty()){
auto n = p1->top(); p1->pop(); r.back().push_back(n->val);
if(zz){
if(n->left) p2->push(n->left);
if(n->right) p2->push(n->right);
}else{
if(n->right) p2->push(n->right);
if(n->left) p2->push(n->left);
}
}
if(Q1.empty() && Q2.empty()) break;
zz=!zz;
r.push_back(vector<int>());
}
return r;
}
};
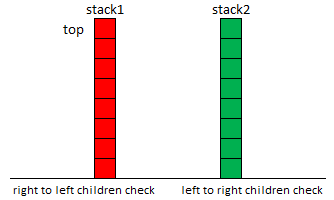
因为容器是stack, push的时候加点和pop的时候加点正好相反.
struct Solution {
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> r;
if (not root) return r;
stack<TreeNode*> R, G;//red and green stack
G.push(root); //!!
while (!R.empty() || !G.empty()) {
if(G.empty()){
r.push_back(vector<int>());
while(!R.empty()){
auto n = R.top(); R.pop(); r.back().push_back(n->val);
if(n->right) G.push(n->right);
if(n->left) G.push(n->left);
}
}
if(R.empty() && !G.empty()){ //!!
r.push_back(vector<int>());
while(!G.empty()){
auto n = G.top(); G.pop(); r.back().push_back(n->val);
if(n->left) R.push(n->left);
if(n->right) R.push(n->right);
}
}
}
return r;
}
};- Algo 2: deque or list
一个数据结构应该就够了.但是不能用queue,必须用dequeue或者list.
struct Solution {
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> r;
if (!root) return r;
deque<TreeNode*> Q;
Q.push_back(root);
int layer=0;
vector<int> v;
while(!Q.empty()){
int count = Q.size();
layer++;//
while(count--){
TreeNode* t;
if(layer&1){
t=Q.front(); Q.pop_front();
if(t->left) Q.push_back(t->left);
if(t->right) Q.push_back(t->right);
}else{
t=Q.back(); Q.pop_back();
if(t->right) Q.push_front(t->right);
if(t->left) Q.push_front(t->left);
}
v.push_back(t->val);
}
r.push_back(v), v.clear();
}
return r;
}
};从前面pop的话,push就必须从后面.(不然变成了stack.) 这里layer的alternate可以用-1 times itself, or a^b=c trick.
14.16 Balanced Binary Tree (Recursion)
https://leetcode.com/problems/balanced-binary-tree/
struct Solution {
bool isBalanced(TreeNode* root) {
if (not root) return true;
return isBalanced(root->left) and isBalanced(root->right) and \
abs(height(root->left)-height(root->right))<=1;
}
int height(TreeNode* root){
if(not root) return 0;
return max(height(root->left), height(root->right))+1;
}
};14.17 297. Serialize and Deserialize Binary Tree
The tricky part is deserialize(*) function.
- DFS
Preorder with delimiter (Recursive)
https://leetcode.com/problems/serialize-and-deserialize-binary-tree/
http://fisherlei.blogspot.com/2013/03/interview-serialize-and-de-serialize.html
序列化的时候首先要考虑反序列化的时候怎么恢复.反序列化最好是从根开始生成树.所以要找一个算法很容易把根找出来.如果把Tree看成graph的话,BFS,DFS都可以满足条件.Tree traversal的preorder是一种DFS. Inorder和postorder既不是BFS也不是DFS.(这样看来preorder还蛮特别的算是树和图知识点的交集.)
在对树进行DFS的同时把节点值放入一个string实现序列化.反序列的时候,输入其实是一个dfs路径,就沿着路走并恢复节点.
Complexity: \(O(N)\)
Preorder with special delimeter can define a uniqe binary tree!!
struct Codec { // 119 ms
list<string> split(string s){ //hand-made string split, return vector,list
list<string> r;
int i=0;
while((i = s.find(',')) != s.npos || !s.empty()){
if(i!=s.npos){
r.push_back(s.substr(0,i));
s = s.substr(i+1);
}else r.push_back(s), s="";
}// after this point, no ',' in string, and string s is empty
return r;
}
string serialize(TreeNode* root) {
if (!root) return "n";
return to_string(root->val) + "," + serialize(root->left) + "," + serialize(root->right);
}
TreeNode* deserialize(string data) {
list<string> r = split(data);
return dfs(r);
}
TreeNode* dfs(list<string>& r){ //反序列化的难点是找root
if (r.empty()) return 0;
if (r.front()=="n"){
r.pop_front();////!!!!
return 0;
}
TreeNode *root = new TreeNode(stoi(r.front()));
r.pop_front();
root->left = dfs(r);
root->right = dfs(r);
return root;
}
};用string function:
struct Codec {
string serialize(TreeNode* root) {
if(!root) return "n";
return to_string(root->val)+","+serialize(root->left)+","+serialize(root->right);
}
TreeNode* deserialize(string data) {
return rec(data);
}
TreeNode* rec(string& s){
if(s[0]=='n'){
s.erase(s.begin());
if(s[0]==',') s.erase(s.begin()); // MIGHT be a comma afer n
return 0;
}
int i=s.find(',');
string t=s.substr(0,i);
s=s.substr(i+1);
TreeNode* nd=new TreeNode(stoi(t));
nd->left=rec(s);
nd->right=rec(s);
return nd;
}
};用istringstream:
struct Codec {
string serialize(TreeNode* root) {
if(!root) return "n";
return to_string(root->val) + "," + serialize(root->left) + "," + serialize(root->right);
}
TreeNode* deserialize(string data) {
istringstream is(data);
return dfs(is);
}
TreeNode* dfs(istringstream& is){
string t;
if(!getline(is, t, ',').eof()){// while is also ok
if(t=="n") return 0;
TreeNode* R=new TreeNode(stoi(t));
R->left=dfs(is);
R->right=dfs(is);
return R;////
}
return 0;
}
};优化:
上面的方法容易实现但不是最优的.二叉树的叶子节点数比内部节点数多一个.所以上图6个cell用了7个null.
优化的方法是把包围叶子节点的连续的null,null用一个token(比如$)表示.单独的null保持原样.这样原树有几个叶节点就节约几个token.
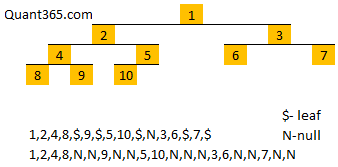
struct Codec { // 33ms, Your runtime beats 83.91% of cpp submissions.
string serialize(TreeNode* root) {
if (root == 0) return "N"; //null marker
if (root->left == 0 && root->right == 0)
return to_string(root->val) + ",$"; // leaf node
return to_string(root->val) + "," + serialize(root->left) + "," + serialize(root->right);
}
TreeNode* deserialize(string data) {
istringstream is(data);
return dfs(is);
}
TreeNode* dfs(istringstream& is) {//return root node from stringstream
string t;
while (getline(is, t, ',')) {
if (t == "$") {
return (TreeNode*)-1;
} else if (t == "N") {
return 0;
} else {
TreeNode* R = new TreeNode(stoi(t));
TreeNode* p = dfs(is);
if (p == (TreeNode*)-1) {
R->left = R->right = 0;
} else {
R->left = p;
R->right = dfs(is);
}
return R;
}
}
return 0;
}
};这个DFS函数有返回值,类似binary tree剥叶子问题返回树的深度.这种有返回值DFS函数的写法都是:
1. 终止条件/base case
2. 先call自己得到返回值,利用返回值构建本层函数的logic
And the delimeter between leaf node and $ can be removed:
string serialize(TreeNode* root) {
if (root == 0) return "N"; //null marker
if (root->left == 0 && root->right == 0)
return to_string(root->val) + "$"; // leaf node
return to_string(root->val)+","+serialize(root->left)+","+serialize(root->right);
}
TreeNode* dfs(istringstream& is) {
string t;
while(getline(is, t, ',')) {
if (t.back() == '$') {
t.pop_back();
return new TreeNode(stoi(t));
} else if (t == "N") { return 0; }
else {
TreeNode* r = new TreeNode(stoi(t));
r->left = dfs(is);
r->right = dfs(is);
return r;
}
}
return 0;
}- BFS
Layer by Layer (Iterative)
http://blog.csdn.net/ljiabin/article/details/49474445
2017(7-9月) 码农类 博士 全职 Facebook - 内推 - 技术电面 |Otherfresh grad应届毕业生
1. LC297 serialize/deserialize BST与原题不一样的是输出是vector,not a string.
2. LC133 Clone Graph与原题不一样的是输入不是一个Node, 而是vector<Node>, 需要clone这个vector里的所有nodes.问面试官所有的nodes是否fully connected他说什么情况都有可能.
http://bit.ly/2vOAjHw
Follow-up
How to test?
http://www.geeksforgeeks.org/serialize-deserialize-binary-tree/N-ary Tree/Trie/(sparse/dense) Graph
http://www.geeksforgeeks.org/serialize-deserialize-n-ary-tree/
In an N-ary tree, there are no designated left and right children. An N-ary tree is represented by storing an array or list of child pointers with every node. The idea is to store an ‘end of children’ marker with every node. The following diagram shows serialization where ‘)’ is used as end of children marker. The diagram is taken from here.
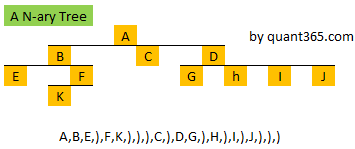
Do it using
parenthesis propertyof DFS
http://www.jiuzhang.com/solutions/binary-tree-serialization/Inorder + Postorder/Preorder
用下面两道题的思路也可以解该题,但是肯定不是最优,因为需要双倍的空间.
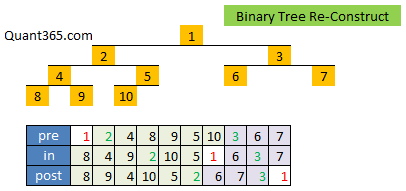
Why in-order doesn’t work?
YouCANNOTfind root with in-order.
14.17.1 105. Construct Binary Tree from Preorder and Inorder Traversal
Given preorder and inorder traversal of a tree, construct the binary tree. Note: You may assume that duplicates do not exist in the tree.
https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
typedef vector<int>::iterator IT;
struct Solution {
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if(preorder.empty()) return 0;
return rec(preorder.begin(), preorder.end(), inorder.begin(), inorder.end());
}
TreeNode* rec(IT pb, IT pe, IT ib, IT ie) {
if(pb==pe) return 0;
TreeNode *r=new TreeNode(*pb);// starting from head
IT t=find(ib, ie, *pb);
int len=t-ib+1;
r->left =rec(pb+1, pb+len, ib, t);
r->right=rec(pb+len, pe, t+1, ie);
return r;
}
};关键是找root. 这里使用了STL算法中的find.
14.17.2 106. Construct Binary Tree from Postorder and Inorder Traversal
Given inorder and postorder traversal of a tree, construct the binary tree. Note: You may assume that duplicates do not exist in the tree.
https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/
struct Solution {
typedef vector<int>::iterator IT;
TreeNode* buildTree(vector<int>& iv, vector<int>& pv) {
if(pv.empty()) return 0;
return rec(iv.begin(),iv.end(),pv.begin(),pv.end());
}
TreeNode* rec(IT ib, IT ie, IT pb, IT pe){
if(ib==ie) return 0; //!!
TreeNode* r= new TreeNode(*(pe-1));
IT t = find(ib, ie, *(pe-1));
r->left = rec(ib,t,pb,pb+(t-ib));
r->right = rec(t+1,ie,pb+(t-ib),pe-1); //!!
return r;
}
};Follow up 2:
- If you are given two traversal sequences, can you construct the binary tree?
It depends on what traversals are given. If one of the traversal methods is Inorder then the tree can be constructed, otherwise not.
Therefore, following combination can uniquely identify a tree.
Inorder and Preorder.
Inorder and Postorder.
Inorder and Level-order.
And following do not:
Postorder and Preorder.
Preorder and Level-order.
Postorder and Level-order.
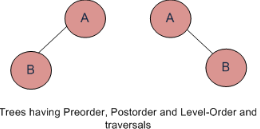
For example, Preorder, Level-order and Postorder traversals are same for the trees given in above diagram.
Preorder Traversal = AB
Postorder Traversal = BA
Level-Order Traversal = AB
So, even if three of them (Pre, Post and Level) are given, the tree can NOT be constructed!!
对BST来说,因为bst的性质,相当于Inorder已经给你了,所以只要知道另外一个就可以重建.
Follow up 3:
证明: why is one traversal not enough for a general tree, (without the information it is a BST)?
Answer: Let’s assume we have n distinct elements. There are \(n!\) possible lists to these n elements, however - the possible number of trees is much larger (\(2*n!\) possible trees for the n elements are all decayed trees, such that node.right=null in every node, thus the tree is actually a list to the right. There are \(n!\) such trees, and another \(n!\) trees where always node.left=null ). Thus, from pigeon hole principle - there is at least one list that generates 2 trees, thus we cannot reconstruct the tree from a single traversal. (QED)
Follow up 4:
- How many different Binary Tree Possible given Preorder Sequence length N?
- How many different BST Possible given N different values elements?
http://stackoverflow.com/questions/16004723/number-of-binary-search-trees-over-n-distinct-elements
Catalan增长的速度接近\(4^n/n^{3/2}\),当n大于5,catalan数大于\(2^n\).
\(Factorial > Catalan > 2^n\)