Chapter 39 Google 2016 12

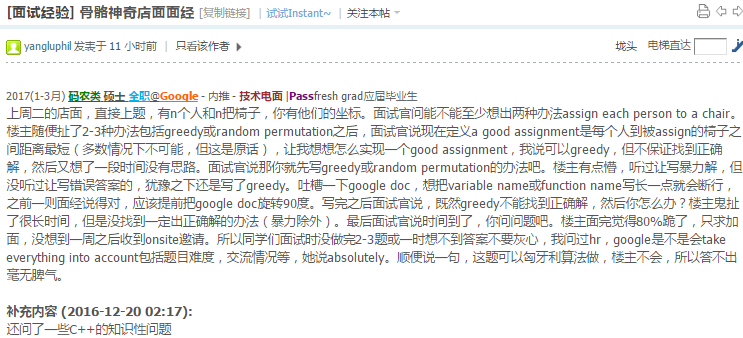
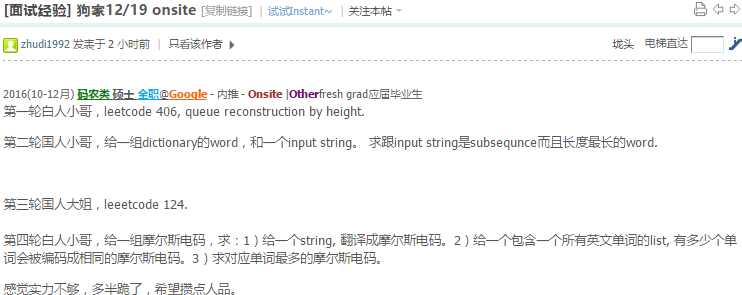
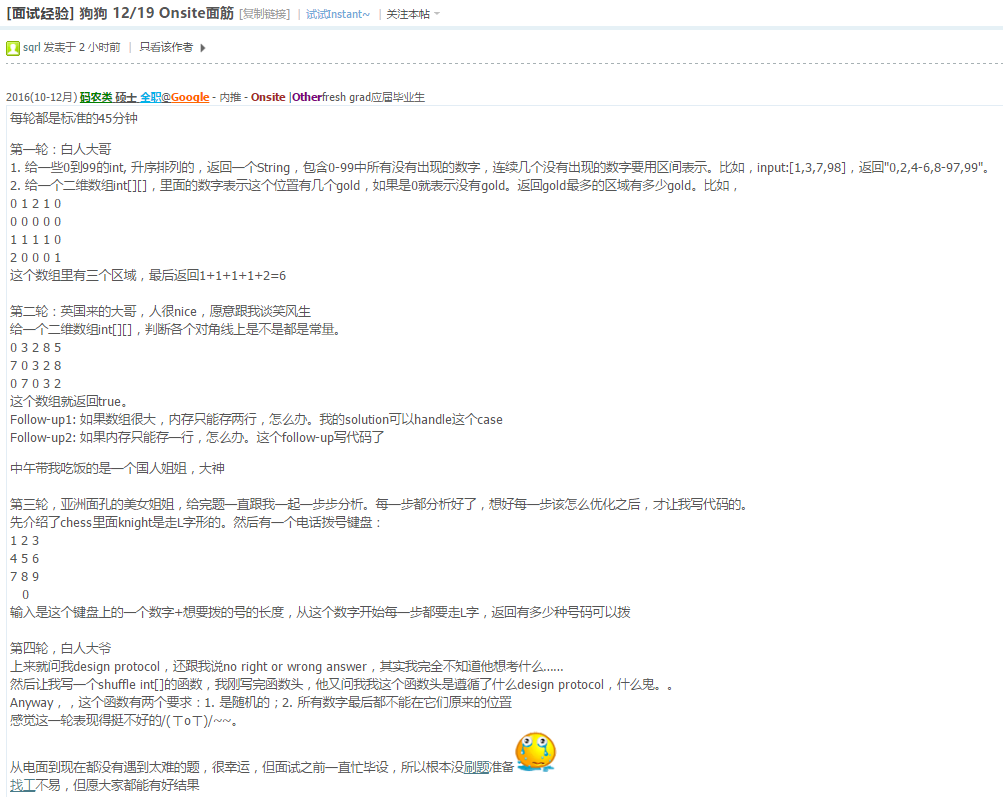
2017(7-9月) 码农类硕士实习 Google - 内推 - 技术电面 |Fail其他
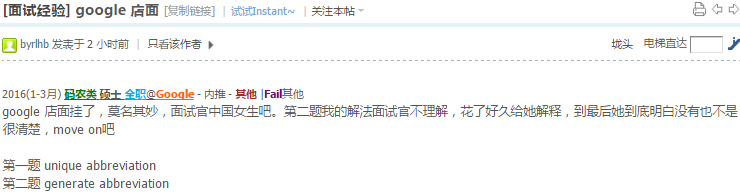
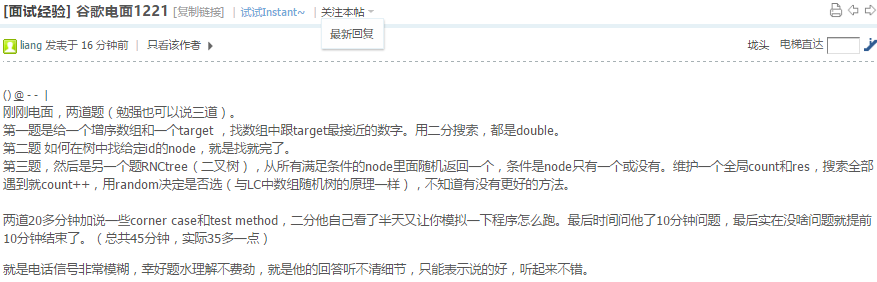
英语不好真是蛋疼,时常要让人打问题…不管了,跪了就跪了,楼主来说说三次面试吧.11.30 两次面试
第一面 warm up 是给出两个区间, 判断是否相交….一行判断…
第二个问题,给了个class 代表的二叉树,有个成员函数要求 binary tree level travesal… 太坑爹了, 他说不能用额外空间不能递归,当时我就傻了,怎么搞,我一直以为他的意思是连成员函数也没法调用,最后没法了,只好问他能不能调用,他说可以……….一头包
第二面这位本土小哥非常热情~~
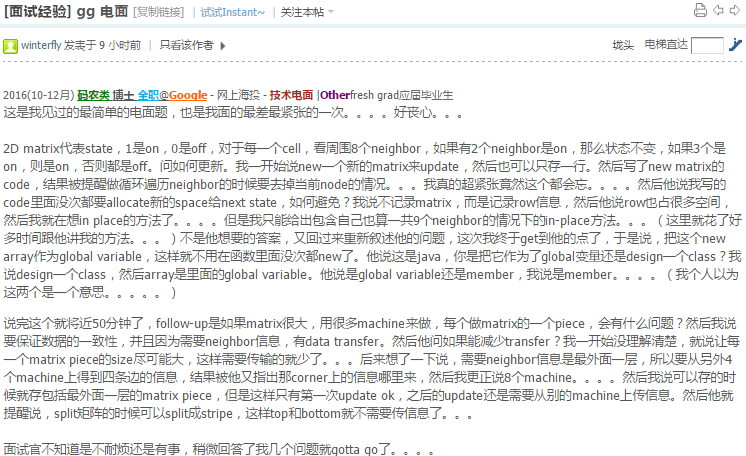
第一个问题,lonely pixel, 给一个nxm的图,只有黑白两种pixel,如果一个黑pixel所在的行和列都只有他,他就是单身的黑pixel,求出所有的单身黑pixel,O(nm),秒之
第二个问题, 进化版, 这回给定参数 N, 要找的黑pixel需要满足,他所在的行列只有N个黑pixel, 并且N行中不同的行中的黑pixel 的位置需要相同, 开头理解错题意了…最后他指了出来,最后没时间,给了个O(n^2m)的,后来想了下应该可以是O(n,m)
然而我最蠢的是最后问他是干什么工作的..尤其是在他开头已经自我介绍过的情况下…. 然后被通知了加面
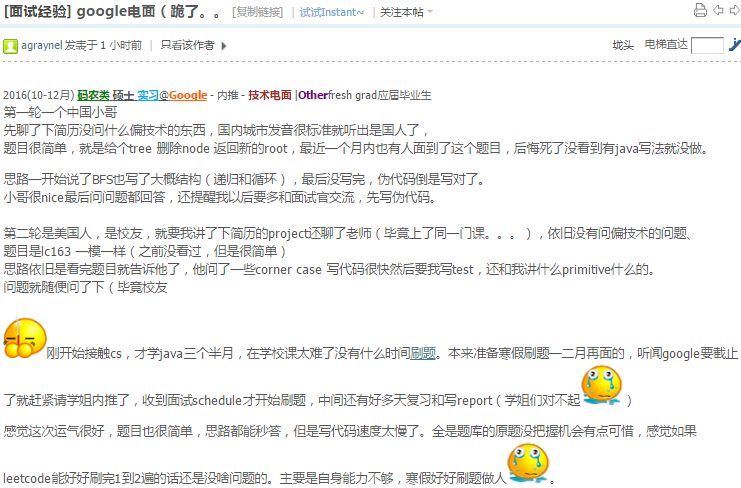
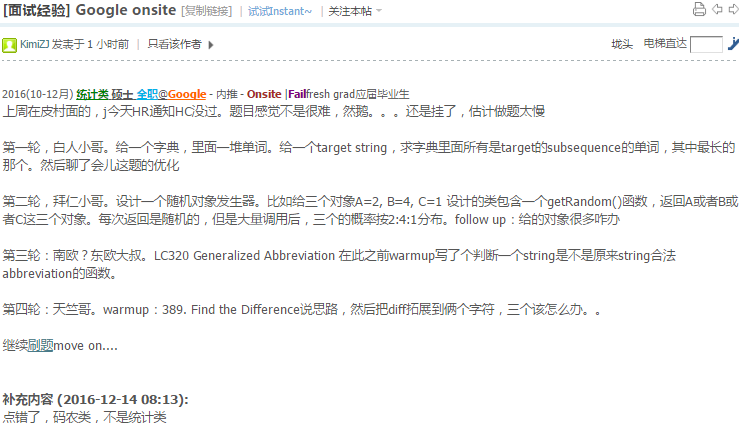
第三面
美国小哥的电话真爆炸,各种噪音,语速又快,听的一头包
第一个问题,非递归前序遍历,秒之
第二个问题,给定二叉树和一个function shouldbeerased(node n). 可以询问节点n是否删除, 然后问删除所有shouldbeerased的节点后,剩余tree的集合,每个tree给个根节点.递归,参数是父节点,当前节点,父节点是否是已存在树的一部分.然后分情况做
挺水的…但是!!!我记错了时间,我还以为我有大把时光可以给小哥好好讲讲我的算法,然而我记错时间了,在我以为还有15分钟时,其实结束了….早知如此,我第一题就不主动提出来给他跑个testcase了,花了我10来分钟.自作孽不可活…..
anyway,move on了,今年好难找实习,希望亚麻能来个oa吧….. http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=216422

39.1 Range Overlap

One line solution: y1<=x2 && x1<=y2

This looks related to interval trichotomy. It is more clear to think in opposite way: how to check if two ranges are not overlapped?

It should be y2<x1 || x2<y1, and by negating it, we get y2>=x1 && x2>=y1, which is the answer.

39.2 Delete Tree

如果某节点被删除,尝试把它自己移除答案子树集合,并把它的左右子树加入答案子树集合,然后递归左右子树,最后返回即可

39.3 Lonely Pixel

39.4 163. Missing Ranges

https://leetcode.com/problems/missing-ranges/

http://blog.csdn.net/xudli/article/details/42290511

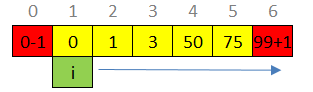
这道题最吊诡的地方是最两端的[lower,upper]要求是inclusive range,但是中间的其他点要求是exclusive(虽然并没有显示的指出来).所以在loop的时候,逻辑容易混乱.为了让loop可以一次过,把lower-1,upper+1加入vector,让它变成一个纯粹的exclusive的点的vector,然后一次loop即可.

陷阱是加减1之后会有int overflow,所以要用一个新的long vector来代替原数组. T,S: \(O(N)\).

struct Solution { // T,S: O(N)
    vector<string> findMissingRanges(vector<int>& ns, int lower, int upper) {
        vector<string> r;
        vector<long> nums(1,lower-1L);
        for(int i: ns) nums.push_back(i);
        nums.push_back(upper+1L);
        for (int i=1;i<nums.size();++i)
            if(nums[i-1]+1>=nums[i]) continue;
            else
                if(nums[i-1]+1==nums[i]-1)
                    r.push_back(to_string(nums[i-1]+1));
                else
                    r.push_back(to_string(nums[i-1]+1)+"->"+to_string(nums[i]-1));
        return r;
    }
};

还有一种方法是单独处理头尾两个节点.如上图,i从1循环到75为止,然后再来看lower和nums[0],upper和nums.back()的关系.这样可以做到Space \(O(1)\).

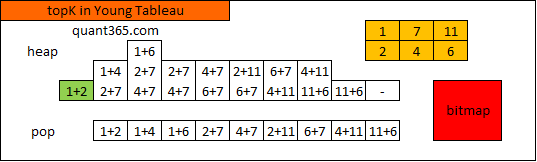
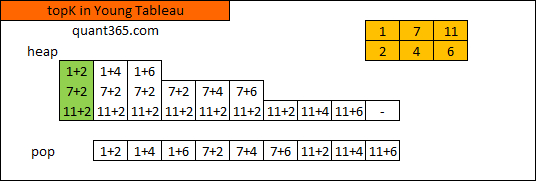
39.5 373. Find K Pairs with Smallest Sums

https://leetcode.com/problems/find-k-pairs-with-smallest-sums/

http://www.cnblogs.com/grandyang/p/5653127.html

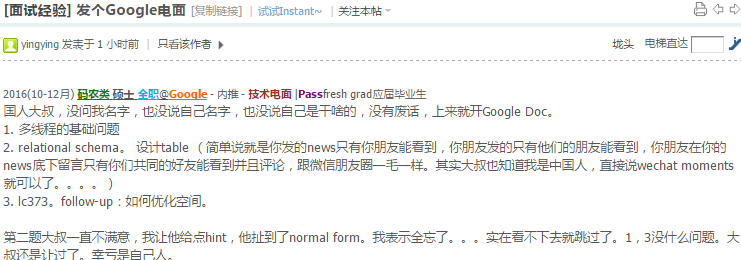
You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k.

Define a pair (u,v) which consists of one element from the first array and one element from the second array.

Find the k pairs (u1,v1),(u2,v2) ...(uk,vk) with the smallest sums.

Example 1:

Given nums1 = [1,7,11], nums2 = [2,4,6],  k = 3
Return: [1,2],[1,4],[1,6]

The first 3 pairs are returned from the sequence:

[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

Young Tableau的应用. 参见: matrix.html#kth-smallest-element-in-a-sorted-matrix

39.5.1 Algo 1

把(a1, b1)丢入堆中,按照元素和排序.
取出堆顶元素,如(ai, bj),把ai,bj相加,输出.把(ai+1, bj), (ai, bj+1)丢入堆
重复2,k次即可.

39.5.2 Algo 2 - Optimization

把(a1, bi), i = 0…n加入堆中
取出最小的那个(ai, bj),把(ai+1, bj)加入堆中
重复2,k次

39.6 Ugly Number I/II, Super Ugly Number

https://leetcode.com/problems/ugly-number/

https://leetcode.com/problems/ugly-number-ii/

参见
https://en.wikipedia.org/wiki/Regular_number#Algorithms
https://oeis.org/A051037

Ugly number的学术名字叫做5-smooth numbers(i.e., numbers whose prime divisors are all <= 5)或者 Hamming Number.

这道题是让你产生第n个ugly number.没有通用公式,而且Space \(O(1)\)是不可能做到.

T:\(O(N)\)应该没得说,但这道题我目前只能想到S:\(O(N)\)的解法. 有点三指针的感觉.

具体做法就是vector<int>r里面放ugly number,先初始化一个1,因为1是规定的.然后用2,3,5不断去乘r里面的数,具体乘哪个,由i,j,k来确定.

好像2,3,5是这个序列的数字发生器.初始值1,就可以generate无穷多个数.

struct Solution { // Your runtime beats 50.49% of cpp submissions. 16ms
    int nthUglyNumber(int n) {
        if(n==1) return 1;
        vector<int> r(n,1);
        int i=0, j=0, k=0, idx=0;
        while(1){
            register int t2=r[i]*2, t3=r[j]*3, t5=r[k]*5;
            int mi = min(min(t2, t3), t5);
            if (mi==t2) i++;
            else if(mi==t3) j++;
            else k++;
            if(mi==r[idx]) continue;
            r[++idx] = mi;
            if(idx+1==n) return mi;
        }
        return 1;//pass compiler check
    }
};

https://leetcode.com/problems/super-ugly-number/

找出第n个超级丑数,思路与找出第n个丑数是一样的.区别仅在与找出第n个丑数时,用三个数字记录中间变量,而在找第n个超级丑数时,用一个数组记录.难点在去重.

Write a program to find the nth super ugly number.

Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of size k. For example, [1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32] is the sequence of the first 12 super ugly numbers given primes = [2, 7, 13, 19] of size 4.

Note:

1 is a super ugly number for any given primes.
The given numbers in primes are in ascending order.
0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000.

https://my.oschina.net/Tsybius2014/blog/547766

T: \(O(NK)\) S: \(O(N+K)\)

首先延续上面的解法,用naive的解法搞定.

struct Solution { // 106ms 83%
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n==1) return 1;
        int K = primes.size(), counter=1;
        vector<int> r(n, 1), idx(K, 0);
        while(counter<n){ // O(N)
            int mi=2147483647; // 8th Mersenne prime
            for(int i=0;i<K;i++) mi = min(mi, primes[i]*r[idx[i]]);//1.find the min
            for(int i=0;i<K;i++) if(mi == primes[i]*r[idx[i]]) idx[i]++;//2.remove dups
            r[counter++]=mi;
        }
        return r.back();
    }
};

第二个去重的循环要一直到底不能break.

比如对下面的输入:

40 [2,3,11,13,17,23,29,31,37,47]

66会有三个dups: 2x33, 3x22, 6x11.

struct Solution { // 106ms 83%
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n==1) return 1;
        int K = primes.size(), counter=1, debug=0;
        vector<int> r(n, 1), idx(K, 0);
        while(counter<n){ // O(N)
            int mi=2147483647; // 8th Mersenne prime
            for(int i=0;i<K;i++) mi = min(mi, primes[i]*r[idx[i]]), debug++;//1.find the min
            for(int i=0;i<K;i++) if(mi == primes[i]*r[idx[i]]) idx[i]++, debug++;//2.remove dups
            r[counter++]=mi;
        } cout << debug << endl;
        return r.back();
    }};

对下面的输入:

10000 [2,3,5,7,11]

debug = 85660

两个不成功的改进:

可以看到上面的方法有很多重复计算primes[i]*r[idx[i]],还用了两个for loop,下面的方法看起来更好.

struct Solution { // 183ms 40%
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n==1) return 1;
        int K = primes.size(), counter=1;
        vector<int> r(n, 1);
        vector<int> idx(K, 0);
        int mi, tmp, p;
        while(counter<n){ // O(N)
            mi=INT_MAX;
            for(int i=0; i<K; i++){ // O(K) find the min and its index
                p= primes[i] * r[idx[i]];
                if(mi > p){ mi = p; tmp=i;}
            }
            idx[tmp]++;
            if(mi>r[counter-1]) r[counter++]=mi;
        }
        return mi;
    }};

不过运行之后,发现更加耗时.节约的乘法和loop并没有带来优化效果.仔细的观察并不是每次while循环counter都加1.去重的低效导致算法退化为\(O(N*K*K)\).

加入调式语句:

struct Solution { // 183ms 40%
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n==1) return 1;
        int K = primes.size(), counter=1;
        vector<int> r(n, 1);
        vector<int> idx(K, 0);
        int mi, tmp, p, debug=0, debug2=0;
        while(counter<n){ // O(N)
            mi=INT_MAX;
            debug++;
            for(int i=0; i<K; i++){ // O(K) find the min and its index
                p= primes[i] * r[idx[i]]; debug2++;
                if(mi > p){ mi = p; tmp=i;}
            }
            idx[tmp]++;
            if(mi>r[counter-1]) r[counter++]=mi;
        }
        cout << debug << "," << debug2 << endl;
        return mi;
    }};

对下面的输入:

10000 [2,3,5,7,11]

debug=35662,debug2=178310.

如果单从语言,特别是非汇编语言(就算是汇编语言一也一样)是没法比较运算符的效率的.现代CPU架构的复杂性,已经很难理论评估计算时间了.如sudo所说,这里面包含了太多细节.粗略估计的话,整数的加减运算参考CPU的频率1个cpu周期,乘法大概是几个CPU周期,除法一般要花费更多时间.浮点运算更复杂一些,开使用了什么FPU.现在如果在乎计算效率的话,不是在乎每个周期做多少运算(当然高效的算法是最重要的),而是优化代码流程,达到满流水线和高cache命中.减少内存访问以及其他的IO.参考:https://www.zhihu.com/question/27555387

网上看到说用index heap把复杂度从\(O(NK)\)降到了\(O(NLogK)\). 其实是不对的. (https://goo.gl/ITLxiE)

复杂度 T: \(O(NKLogK)\) S: \(O(N+K)\)

struct node{
    int val=0, idx=0, p=0;
    node(int val_, int idx_, int p_):val(val_),idx(idx_),p(p_){}
};
struct comp{bool operator()(node* x, node* y){return x->val > y->val;}};
struct Solution { // 276 ms
    int nthSuperUglyNumber(int n, vector<int>& p) {
        if(n==1) return 1;
        priority_queue<node*,vector<node*>,comp> h;
        for(int i: p){h.push(new node{i,1,i});} // O(K)
        vector<int> r(n,1);
        node* pn;
        int count=0; // debug
        for (int i=1; i<n; ++i) { // O(N)
            r[i] = h.top()->val;
            do{ // ??? K
                count++;
                pn = h.top(); h.pop(); // O(LogK)
                pn->val = pn->p*r[pn->idx++];
                h.push(pn); // O(LogK)
            } while (h.top()->val == r[i]);
        }
        cout << count << "\n";
        return r[n-1];
    }};

do-while loop的复杂度一眼看不出来,其实是K. 我增加了一个count来验证想法. N越大,count的数量越趋向于\(NK\).

如上图越往后走,重复的数字越多,重复的次数也越多.

对下面的输入:

10000 [2,3,5,7,11]

couter的数值等于35665. 这就是为什么这个算法慢的原因,并不是priority queue不快,而是算法本身的问题.

当然priority_queue本身也不快,尤其如果用priority_queue<node*,deque<node*>,comp> h;的话,时间会翻倍到500多ms.

http://www.cplusplus.com/reference/queue/priority_queue/pop/
http://www.cplusplus.com/reference/algorithm/pop_heap/
http://www.cplusplus.com/reference/algorithm/push_heap/

Others:

https://www.quora.com/Why-do-we-use-base-60-for-time

时钟周期、振荡周期、机器周期、CPU周期、状态周期、指令周期、总线周期、任务周期
http://www.cnblogs.com/MuyouSome/p/3175806.html