Chapter 8 Matrix
Matrix is an extension of array in 2-dimension. The algorithms are also the extension of array algorithms in 2-dimension.
Common topics are:
- matrix manipulation(rotate, printing, multiplication)
- sparse matrix(CCS/CRS)
- matrix as graph(solve with DFS/BFS/Memorization)
- linear algebra matrix
- sorted matrix/Young tableau(2D binary search)
- rolling matrix
8.1 Basics
8.1.1 Conventions
C - size of columns
R - size of rows
N - use `N` to represent the length of square matrix.
i - index of row
j - index of column8.1.2 Index Conversion
From Matrix Index (\(i,j\)) to 1D Array Index \(idx\) is:
From 1D Array Index \(idx\) to Matrix Index (\(i,j\)):
No matter which type of index conversion, i and j are only related to C, not R.
if(m.empty() || m[0].empty()) return;
int R=m.size(), C=m[0].size();8.1.3 Diagonals
- Major or Main diagonal(i==j)

Off-diagonalsare the cells not in main diagonal.Minor or Anti diagonal (\(i+j=N-1\))

Refer to: https://en.wikipedia.org/wiki/Main_diagonal
A matrix M with RxC squares has R+C-1 major and minor diagonals. At cell M[i, j], the main diagonal index is \((R - 1) - (i-j)\), and the anti-diagonal index is \(i+j\)

Index of Major Diagonals
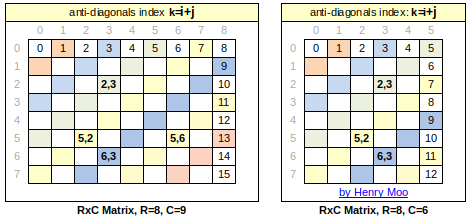
Index of Minor Diagonals
For example: (5,2) => (major)8-1-(5-2)==4, (minor) 5+2==7
8.2 562. Longest Line of Consecutive One in Matrix
Given a 01 matrix M, find the longest line of consecutive one in the matrix. The line could be horizontal, vertical, diagonal or anti-diagonal.
Example:
Input:
[[0,1,1,0],
[0,1,1,0],
[0,0,0,1]]
Output: 3Hint: The number of elements in the given matrix will not exceed 10,000.
https://leetcode.com/problems/longest-line-of-consecutive-one-in-matrix
#define VVI vector<vector<int>> //Your runtime beats 78.84 % of cpp submissions.
int horizon(VVI& M, int R, int C){
int r=0;
for(int i=0;i<R;++i)
for(int j=0, t=0;j<C;++j)
if(M[i][j]) t++, r=max(r,t); else t=0;
return r;
}
int vertical(VVI& M, int R, int C){
int r=0;
for(int j=0;j<C;++j)
for(int i=0, t=0;i<R;++i)
if(M[i][j]) t++, r=max(r,t); else t=0;
return r;
}
int diagonal(VVI& M, int R, int C){ // \\
int r=0;
for(int k=R-1;k>=0;--k)
for(int i=k,j=0,t=0;i<R&&j<C;++i,++j)
if(M[i][j]) t++,r=max(r,t); else t=0;
for(int k=1;k<C;++k)
for(int j=k,i=0,t=0;i<R&&j<C;++i,++j)
if(M[i][j]) t++,r=max(r,t); else t=0;
return r;
}
int antidiag(VVI& M, int R, int C){ // //
int r=0;
for(int k=R-1;k>=0;--k)
for(int i=k,j=C-1,t=0; i<R&&j>=0; ++i,--j)
if(M[i][j]) t++,r=max(r,t); else t=0;
for(int k=C-2;k>=0;--k)
for(int j=k, i=0,t=0; i<R&&j>=0; ++i,--j)
if(M[i][j]) t++,r=max(r,t); else t=0;
return r;
}
struct Solution {
int longestLine(VVI& M) {
int R=M.size(), C;
if(R==0 || (C=M[0].size())==0) return 0;
return max( max(horizon(M,R,C), vertical(M,R,C)),
max(diagonal(M,R,C), antidiag(M,R,C)));
}
};以diagonal traversal为例,关键是找到起始点,然后i++,j++,而且还得控制住新点的范围在matrix之内. 起始点分为两个部分,一个是最左边的一列,一个是最上边的一行.所以整个函数的分为两个大for loop.
int diagonal(VVI& M, int R, int C){ // \\
int r=0;
for(int k=R-1;k>=0;--k)
for(int i=k,j=0,t=0;i<R&&j<C;++i,++j)
if(M[i][j]) t++,r=max(r,t); else t=0;
for(int k=1;k<C;++k)
for(int j=k,i=0,t=0;i<R&&j<C;++i,++j)
if(M[i][j]) t++,r=max(r,t); else t=0;
return r;
}上面diagonal和antidiag分为两个阶段.It is recommended no matter in production or interview!!!
其实可以简化.比如对diagonal函数编码的简化:
K: 0,1,2…,R+C-2
istart: R-1,R-2…0,0,0…0
iend: R-1,R-1,…R-1,R-2,R-3,…2,1,0
所以istart=max(0,R-1-k), iend=min(R-1,R+C-2-k), 相应函数可以用如下代码实现:
int diagonal(VVI& M, int R, int C){ // ... beats 73.44 % of cpp submissions.
int r=0;
for (int k=0; k<R+C-1; ++k)
for(int i=max(0,R-1-k), t=0; i<=min(R-1,R+C-2-k); ++i)
if(M[i][k-R+1+i]) t++, r=max(r,t); else t=0;
return r;
}
int antidiag(VVI& M, int R, int C){
int r=0;
for (int k=0; k< R+C-1; ++k)
for(int i=min(k, R-1), t=0; i>=max(0, k-C+1); --i)
if(M[i][k-i]) t++,r=max(r,t); else t=0;
return r;
}代码简洁了但是速度慢了一点点.
struct Solution {
int longestLine(vector<vector<int>>& M) {
if(M.empty() || M[0].empty()) return 0;
int R=M.size(), C=M[0].size();
int r=0;
for(int i=0;i<R;i++)
for(int j=0,t=0;j<C;j++)
t=(M[i][j]==1)?(t+1):0, r=max(t,r);
for(int j=0;j<C;j++)
for(int i=0,t=0;i<R;i++)
t=(M[i][j]==1)?(t+1):0, r=max(t,r);
for(int k=0; k<R+C-1; k++)
for(int i=max(0,R-1-k),t=0; i<=min(R-1,R+C-2-k); ++i) ////!!!!
t=M[i][k-R+1+i]==1?(t+1):0, r=max(t,r);
for(int k=0; k<R+C-1; k++)
for(int i=min(k, R-1), t=0; i>=max(0, k-C+1); --i) ////!!!!
t=M[i][k-i]==1?(t+1):0, r=max(t,r);
return r;
}
};类似的题目还有: Diagonal Traverse
8.3 498. Diagonal Traverse
Given a matrix of M x N elements (M rows, N columns), return all elements of the matrix in diagonal order as shown in the below image.
Example:
Input:
[[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]]
Output: [1,2,4,7,5,3,6,8,9]Explanation:

https://leetcode.com/problems/diagonal-traverse/
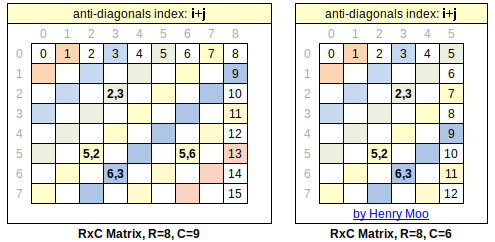
Anti-diagonal Way Matrix Traversal
Anti-diagonal Matrix在同一层的i,j之和相等,就等于anti-diagonal array的index k. We can use this. The crux of the problem is to find start and end of index i.
When moving up, the index i starts from 0 to R-1, actually min(k,R-1).
when moving down, the index i starts from 0 to R-1:
k==[1,C-1], i=0; k==[C,R+C-2], i=1,2…R-1. ==> max(0,k-C+1)
所以很容易写出下面的代码:
struct Solution {
vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
if (matrix.empty() || matrix[0].empty()) return {};
int R = matrix.size(), C = matrix[0].size(), t = 0;
vector<int> r(R*C);
for (int k=0; k< R+C-1; ++k) {
int low = max(0, k-C+1), high = min(k, R-1);
if (i%2 == 0) // North East Up
for(int i=high; i>=low; --i) r[t++] = matrix[i][k-i];
else // South West Down
for(int i=low; i<=high; ++i) r[t++] = matrix[i][k-i];
}
return r;
}
};8.4 Spiral Matrix
 https://leetcode.com/problems/spiral-matrix/
https://leetcode.com/problems/spiral-matrix/
8.4.1 Algo 1: Recursion
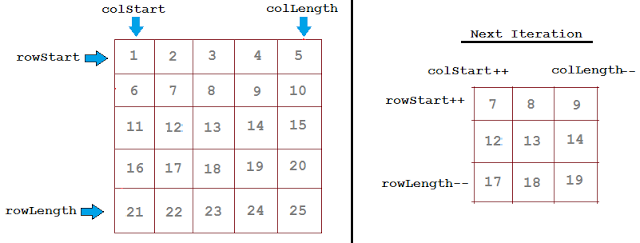
http://javabypatel.blogspot.in/2016/11/print-matrix-in-spiral-order-recursion.html
8.4.2 Algo 2: Iteration
就是把matrix一层层剥开的过程.要注意行列数奇偶对程序的影响.
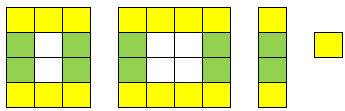
struct Solution {
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> r;
if (matrix.empty() || matrix[0].empty()) return r;
int R = matrix.size(), C = matrix[0].size();
bool odd = (R & 1) || (C & 1);
for (int i = 0; i<(min(R, C) + (int)odd) / 2; ++i) { // i+1是剥掉的层数,i=0是剥第一层
for (int j = i; j<C - i; ++j) r.push_back(matrix[i][j]);
for (int j = i + 1; j<R - 1 - i; ++j) r.push_back(matrix[j][C - 1 - i]);
if (R - 1 - i != i) { for (int j = C - 1 - i; j >= i; --j) r.push_back(matrix[R - 1 - i][j]); }
if (C - 1 - i != i) { for (int j = R - 2 - i; j>i; --j) r.push_back(matrix[j][i]); }
}
return r;
}
};8.5 59. Spiral Matrix II
Given an integer n, generate a square matrix filled with elements from 1 to n2 in spiral order.
For example, Given n = 3, you should return the following matrix:
[
[ 1, 2, 3 ],
[ 8, 9, 4 ],
[ 7, 6, 5 ]
]https://leetcode.com/problems/spiral-matrix-ii/
II比I简单,一样的按层访问法.由于是正方形矩阵,当n为奇数时,最后只会剩下一个数字即matrix[n/2][n/2],最后不要忘记补填上这个数字.
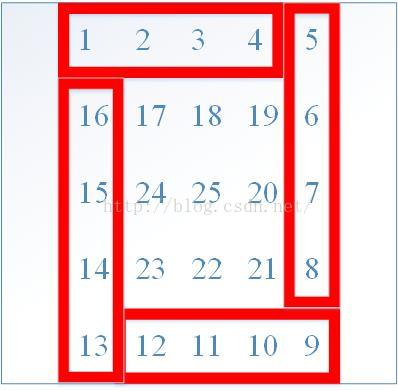
class Solution {
public:
vector<vector<int> > generateMatrix(int n) {
vector<vector<int>> ret(n,vector<int>(n,0));
int nlvl = n/2;
int val = 1;
for(int i=0; i<nlvl; i++) {
int last = n-1-i;
for(int j=i; j<last; j++)
ret[i][j] = val++;
for(int j=i; j<last; j++)
ret[j][last] = val++;
for(int j=last; j>i; j--)
ret[last][j] = val++;
for(int j=last; j>i; j--)
ret[j][i] = val++;
}
if(n%2==1) ret[n/2][n/2] = val;
return ret;
}
};class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> r(n,vector<int>(n));
int v=1;
for(int i=0;i<n/2;i++){
for(int j=i;j<n-1-i;j++) r[i][j]=v++;
for(int j=i;j<n-1-i;j++) r[j][n-1-i]=v++;
for(int j=n-1-i;j>i;j--) r[n-1-i][j]=v++;
for(int j=n-1-i;j>i;j--) r[j][i]=v++;
}
if(n&1) r[n/2][n/2]=v;
return r;
}
};8.6 Young Tableau
Sorted matrix can be considered as extension of sorted array, or a binary search tree with root in bottom left or top right corner. It is sorted not only in each row and column, but also in main diagonal.
M[0][0]is always the minimum, andM[R-1][C-1]always maximum.
Ref:
- http://noalgo.info/397.html
- http://blog.csdn.net/michealmeng555/article/details/2489923
- http://taop.marchtea.com/04.02.html
- http://www.xuebuyuan.com/1536579.html
- http://poj.org/problem?id=1825
- http://shmilyaw-hotmail-com.iteye.com/blog/1721524
- http://www.lai18.com/content/1286275.html
杨氏矩阵(Young Tableau)是一个很奇妙的数据结构,他类似于堆的结构,又类似于BST的结构,对于查找某些元素,它优于堆;对于插入、删除它比BST更方便.
Heap不可以查找元素,YT可以!
8.8 Rotate Image/Matrix
 https://leetcode.com/problems/rotate-image/
https://leetcode.com/problems/rotate-image/
http://www.tangjikai.com/algorithms/leetcode-48-rotate-image
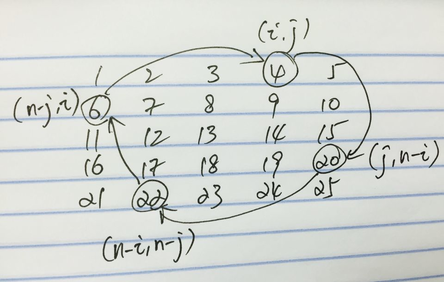
也是用剥洋葱的方法,因为是square matrix所以不用考虑太多edge case.这题的难点在搞清楚点在旋转时候的映射关系.
具体旋转的时候可以有两种方式.比如开始旋转的时候可以从M[0][1 ~ N-1]开始旋转,也可以从M[0][0 ~ N-2]开始.
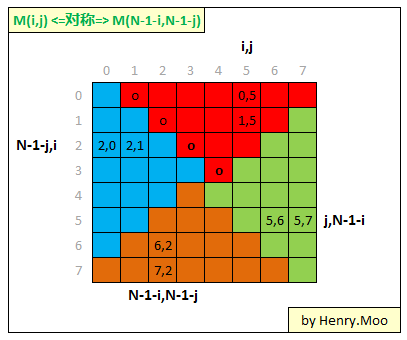
struct Solution {
void rotate(vector<vector<int>>& matrix) {
int N = matrix.size();
for (int i = 0; i<N / 2 + 1; ++i) {
for (int j = 1 + i; j<N - i; ++j) {////!!!!
int tmp = matrix[j][N - 1 - i];
matrix[j][N - 1 - i] = matrix[i][j];
matrix[i][j] = matrix[N - 1 - j][i];
matrix[N - 1 - j][i] = matrix[N - 1 - i][N - 1 - j];
matrix[N - 1 - i][N - 1 - j] = tmp;
}
}
}
};Complexity: \(O(n^2)\) time, \(O(1)\) space
If R is not equal to C, we should be able to rotate image too, but we can not do it inplace.
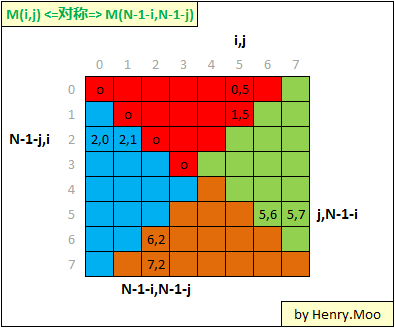
struct Solution {
void rotate(vector<vector<int>>& matrix) {
int N = matrix.size();
for (int i = 0; i<N / 2 + 1; ++i) {
for (int j = i; j<N - i - 1; ++j) {////!!!!
int tmp = matrix[j][N - 1 - i];
matrix[j][N - 1 - i] = matrix[i][j];
matrix[i][j] = matrix[N - 1 - j][i];
matrix[N - 1 - j][i] = matrix[N - 1 - i][N - 1 - j];
matrix[N - 1 - i][N - 1 - j] = tmp;
}
}
}
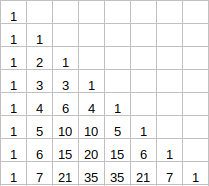
};8.9 Pascal Triangle
Pascal Triangle is actually a Lower Triangular Matrix.
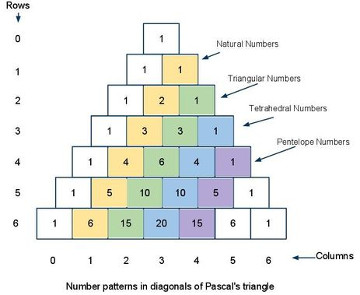
- Pascal’s Triangle
 https://leetcode.com/problems/pascals-triangle/
https://leetcode.com/problems/pascals-triangle/
按定义做: 除了最后一个元素是1外, 每一层的第i个位置,等于上一层第i-1与第i个位置之和.
struct Solution {
vector<vector<int>> generate(int numRows) {
vector<vector<int>> r(numRows, {1});
for(int i=1, j; i<numRows; ++i){
r[i].resize(i+1);
for(j=1; j<i; ++j)
r[i][j]=r[i-1][j-1]+r[i-1][j];
r[i][j]=1;
}
return r;
}
};- Pascal’s Triangle II
 https://leetcode.com/problems/pascals-triangle-ii/
https://leetcode.com/problems/pascals-triangle-ii/
Pascal Triangle’s one row can be calculated by the previous row, so we can use a rolling array like that in DP.
\(T: O(N^2), S: O(N)\)
struct Solution {
vector<int> getRow(int k) {
if(k<0) return {};
vector<int> t(k+1,1), r=t;
for(int i=1; i<k; ++i){
for(int j=1; j<i+1; ++j)
r[j] = t[j-1] + t[j];
t=r;
}
return r;
}
};Actually there is a math forumla for nth row: https://math.stackexchange.com/questions/1154955/is-there-an-equation-that-represents-the-nth-row-in-pascals-triangle
\({n \choose k} = \frac{n!}{k!(n-k)!}\)
Also, pascal triangle is symmetric, we can calculate half and then copy!
8.10 120. Minimum Path Sum of Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
https://leetcode.com/problems/triangle
这个形状类似杨辉三角. M[i][j]的下一行相邻的点是M[i+1][j]和M[i+1][j+1]. 如果是树直接递归.
这个就是用tree的recusive思想来做,会超时,因为有太多重复计算:
class Solution {
int R, C;
public:
int minimumTotal(vector<vector<int>>& t) {
if((R=t.size())==0 || (C=t[0].size())==0) return 0;
int k=min(rec(t,1,0), rec(t,1,1));
return t[0][0] + (k==INT_MAX?0:k);
}
int rec(vector<vector<int>>& t, int i, int j){
if(i>=R || j>=t[i].size()) return INT_MAX;
int k=min(rec(t,i+1,j), rec(t,i+1,j+1));
return t[i][j] + (k==INT_MAX?0:k);
}
};但是这种情况,可以用DP的思想做,bottom up或者top down都行:

http://blog.csdn.net/nk_test/article/details/49456237

struct Solution {
int minimumTotal(vector<vector<int> > &triangle) {
for (int i = triangle.size() - 2; i >= 0; --i)
for (int j = 0; j <= i; ++j){
triangle[i][j] +=min(triangle[i+1][j+1],triangle[i+1][j]);
}
return triangle[0][0];
}
};- Path Sum IV这道题就是用top down的方法: graph
8.11 64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
Example 1:
[[1,3,1],
[1,5,1],
[4,2,1]]Given the above grid map, return 7. Because the path 1→3→1→1→1 minimizes the sum.
https://leetcode.com/problems/minimum-path-sum/
This is a typical DP problem. Suppose the minimum path sum of arriving at point (i, j) is S[i][j], then the state equation is S[i][j] = min(S[i - 1][j], S[i][j - 1]) + grid[i][j].
Well, some boundary conditions need to be handled. The boundary conditions happen on the topmost row (S[i - 1][j] does not exist) and the leftmost column (S[i][j - 1] does not exist). Suppose grid is like [1, 1, 1, 1], then the minimum sum to arrive at each point is simply an accumulation of previous points and the result is [1, 2, 3, 4].
Now we can write down the following (unoptimized) code.
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int> > sum(m, vector<int>(n, grid[0][0]));
for (int i = 1; i < m; i++)
sum[i][0] = sum[i - 1][0] + grid[i][0];
for (int j = 1; j < n; j++)
sum[0][j] = sum[0][j - 1] + grid[0][j];
for (int i = 1; i < m; i++)
for (int j = 1; j < n; j++)
sum[i][j] = min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j];
return sum[m - 1][n - 1];
}
};As can be seen, each time when we update sum[i][j], we only need sum[i - 1][j] (at the current column) and sum[i][j - 1] (at the left column). So we need not maintain the full m*n matrix. Maintaining two columns is enough and now we have the following code.
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> pre(m, grid[0][0]);
vector<int> cur(m, 0);
for (int i = 1; i < m; i++)
pre[i] = pre[i - 1] + grid[i][0];
for (int j = 1; j < n; j++) {
cur[0] = pre[0] + grid[0][j];
for (int i = 1; i < m; i++)
cur[i] = min(cur[i - 1], pre[i]) + grid[i][j];
swap(pre, cur);
}
return pre[m - 1];
}
};Further inspecting the above code, it can be seen that maintaining pre is for recovering pre[i], which is simply cur[i] before its update. So it is enough to use only one vector. Now the space is further optimized and the code also gets shorter.
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> cur(m, grid[0][0]);
for (int i = 1; i < m; i++)
cur[i] = cur[i - 1] + grid[i][0];
for (int j = 1; j < n; j++) {
cur[0] += grid[0][j];
for (int i = 1; i < m; i++)
cur[i] = min(cur[i - 1], cur[i]) + grid[i][j];
}
return cur[m - 1];
}
};Video: https://youtu.be/bEcW6QqgXvM
8.12 Sparse Matrix
Refer to P.75 of Numerical Recipes 3rd Edition.
Sparse Matrix Storage: linkedin-2017-03
8.13 Sparse Matrix Multiplication
 https://leetcode.com/problems/sparse-matrix-multiplication/
https://leetcode.com/problems/sparse-matrix-multiplication/
http://www.cnblogs.com/EdwardLiu/p/5090563.html
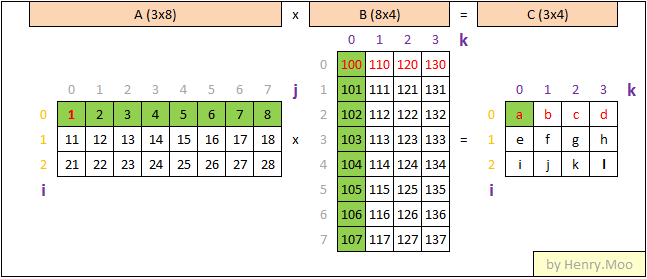
先写处矩阵乘法通式:
C=A*B
=> C[i][k] = A[i][0-j]*B[0-j][k]这个式子本身是对j的循环.
然后要想得到C[i][k]外面肯定是i,k的两重循环,所以是三重循环总共.
vector<vector<int>> multiply(vector<vector<int>>& A, vector<vector<int>>& B) {
int R1 = A.size(), C1 = A[0].size(), /*R2 = B.size(),*/C2 = B[0].size();
vector<vector<int>> r(R1, vector<int>(C2));
for (int i = 0; i<R1; ++i)
for (int j = 0; j<C1; ++j)
if (A[i][j] != 0)//NOTE
for (int k = 0; k<C2; ++k)
r[i][k] += A[i][j] * B[j][k];
return r;
}Note: 这里A[i][j]已知道,如果是0,可以直接continue pass下面的loop.
\(R_2\) is redundant, because \(R_2=C_1\).
Another Solution: http://www.cs.cmu.edu/~scandal/cacm/node9.html
 这个式子是预设A是sparse matrix,其实并不需要B是sparse matrix. 如果告诉A是dense,and B才是sparse matrix,怎么做呢?
这个式子是预设A是sparse matrix,其实并不需要B是sparse matrix. 如果告诉A是dense,and B才是sparse matrix,怎么做呢?
struct Solution {
vector<vector<int>> multiply(vector<vector<int>>& A, vector<vector<int>>& B) {
int ra = A.size(), ca = A[0].size(), cb = B[0].size();
vector<vector<int>> r(ra, vector<int>(cb, 0));
for (int j = 0; j<ca; ++j) {
for (int k = 0; k<cb; ++k) {
if (B[j][k] == 0) continue;////
for (int i = 0; i<ra; ++i) {
r[i][k] += A[i][j] * B[j][k];
}
}
}
return r;
}
};其实如果把第5行和第6行互换也正确. 最这种多重循环,循环层之间没有logic的情况来说,循环层可以互换,而不影响结果. 这里我们根据需要进行交换,加入continue的条件,优化了程序. 这才是这道题的精髓思想.
这道题可以和All pair shortest path’s Floyd Warshall算法求transitive closure联系起来.同样是\(O(N^3)\)的复杂度.参见CLRS P686 - Shortest paths and matrix multiplication.
8.14 CCS (Compressed Column Storage)
8.14.2 Deletion Row and Column
http://www.1point3acres.com/bbs/thread-212960-2-1.html
(Google)第四轮白人大叔,问如何表示稀疏矩阵,一开始可以用两个hash table解决,一个的key 是行数,value是一个key为列数value为值的hash table,另一个是key为列数,value是一个key 为行数value为值的hashtable,follow up,如果想要整行,整列删除,设值该用什么结构?没答上来,应该是用
Orthogonal List(十字链表)补充一下,这道问题还需要写将矩阵整行整列设为某个值的函数,你说得好像也有道理.. 这里需要用到两个hash,hash(row, hash(col, val)), hash(col, hash(row, val)),时间复杂度是一样,不过因为要从两个里面都插入或者删除,代码应该还是十字链表应该要简洁一些
8.15 Search a 2D Matrix I
 https://leetcode.com/problems/search-a-2d-matrix/
https://leetcode.com/problems/search-a-2d-matrix/
struct Solution {
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.empty() || matrix[0].empty()) return false;
int R=matrix.size(), C=matrix[0].size(), l=0, r=R*C-1, mid=0;
while(l<=r){
mid = l+((r-l)>>1);
if (matrix[mid/C][mid%C]==target) return true;
else if (matrix[mid/C][mid%C]<target) l = mid+1;
else r = mid-1;
}
return false;
}
};This is binary search with time complexity of \(O(R*C)\).
8.16 Search a 2D Matrix II
8.16.1 Question 1 - return found not not
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
Integers in each row are sorted in ascending from left to right. Integers in each column are sorted in ascending from top to bottom. For example, consider the following matrix:
[ [1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]]Given target = 5, return true. Given target = 20, return false.
 https://leetcode.com/problems/search-a-2d-matrix-ii/
https://leetcode.com/problems/search-a-2d-matrix-ii/
8.16.1.1 Method 1 - Saddleback Search
You can search from either bottom left or top right cell of the matrix. The following code is starting from bottom left:
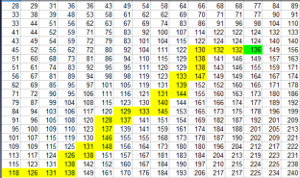
struct Solution { //Young Tableau O(C+R)
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int R = matrix.size(), C = matrix[0].size(), i = R-1, j = 0;
while(i>=0 and j<C)
if (matrix[i][j]<target) ++j;
else if(matrix[i][j]>target) --i;
else return true;
return false;
}
};Note: This is not binary search. Time complexity is \(O(C+R)\).
This is not binary search. Time complexity is \(O(C+R)\).
8.16.1.2 Method 2 - Quad Partition
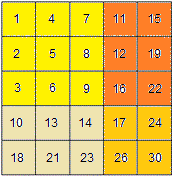
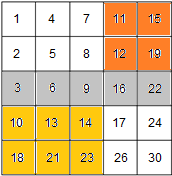
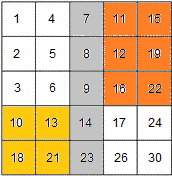
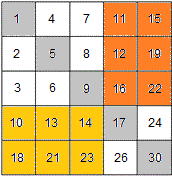
注意对复杂度的分析:
http://articles.leetcode.com/searching-2d-sorted-matrix-part-ii
http://articles.leetcode.com/searching-2d-sorted-matrix-part-iii
Search for an element in a matrix. Rows and columns of the matrix are sorted in ascending order.
eg. matrix
[1 14 25 35]
[2 16 28 38]
[5 20 28 40]
[16 22 38 41] search for 38.
The interviewer was looking for a solution better than O(n+m). He didn’t want a solution which starts searching from the left bottom and go to right or above according to the key value to search. That solution has O(n+m) worst complexity, where n is row count and m is column count.
8.16.2 Question 2 - return the occurrence
Write an efficient algorithm that searches for a value in an m x n matrix, return the occurrence of it.
This matrix has the following properties:
- Integers in each row are sorted from left to right.
- Integers in each column are sorted from up to bottom.
No duplicate integers in each row or column. Example, consider the following matrix:
[ [1, 3, 5, 7],
[2, 4, 7, 8],
[3, 5, 9, 10]]Given target = 3, return 2.
http://www.lintcode.com/en/problem/search-a-2d-matrix-ii/
In this question, it is possible that multiple cells are equal to target.
struct Solution {
int searchMatrix(vector<vector<int> > &matrix, int target) {
if(matrix.empty() or matrix[0].empty()) return 0;
int R=matrix.size(), C=matrix[0].size(), i=R-1, j=0, count=0;
//while(i>=0 and i<R and j>=0 and j<C){
while(i>=0 and j<C){
if (matrix[i][j]==target) --i, ++j, ++count;////!!!!
else if(matrix[i][j]>target) --i;
else ++j;
}
return count;
}
};8.17 378. Kth Smallest Element in a Sorted Matrix
Given a n x n matrix where each of the rows and columns are sorted in ascending order, find the kth smallest element in the matrix.
Note that it is the kth smallest element in the sorted order, not the kth distinct element.
Example:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8, return 13.
matrix = [
[1 ,5 ,7],
[3 ,7 ,8],
[4 ,8 ,9],
]
k=4, return 5.Note: You may assume k is always valid, 1 <= k <= \(n^2\).
 https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/
https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/
https://www.hrwhisper.me/leetcode-kth-smallest-element-sorted-matrix/
8.17.1 Algo 1 - Binary Search, T: O(NlogX)
For any sub-matrix \(X\), the smallest element is the \(X[0][0]\) and the biggest element is \(X[R-1][C-1]\). according to this feature, we can write a 2-D binary search method to find Kth smallest element in a sorted matrix.
similar problems include:
- find kth element in an array
- find kth element in a BST
T: \(O(NLogX)\) where \(X=max - min\)
struct Solution {
int kthSmallest(vector<vector<int>>& matrix, int k) { // 99.07%
int R = matrix.size();
int l = matrix[0][0], r = matrix[R - 1][R - 1];
while (l <= r){ // O(LogX)
int m = l + (r - l)/2;
auto pr = lower_eq(matrix, m, R);
if(pr.second && pr.first==k){return m;} // optimization
if (pr.first < k) l = m + 1; else r = m-1;
}
return l;
}
pair<int,bool> lower_eq(vector<vector<int>>& matrix, int m, int N){// O(2N=R+C)
int i = N - 1, j = 0, count = 0, found=false;
while (i >= 0 && j < N) {
if (matrix[i][j] < m) j++, count += i+1;
else if(matrix[i][j] == m) j++, count += i+1, found=true;
else i--;
}
return {count,found};
}
};因为是ascending order,17行其实还可以加上i–.但是leetcode的test case有一个错误,出现了一个non-descending order的case,所以没法通过.
The key point is when l==r, the mid must exist in the matrix, because there must exist a solution for the problem.
8.17.2 Algo 2 - Heap
其实young tableau和heap非常相似. 这是上面的图的Young Tableau的树的表示. 它相当于两颗heap树从bottom焊接上了.
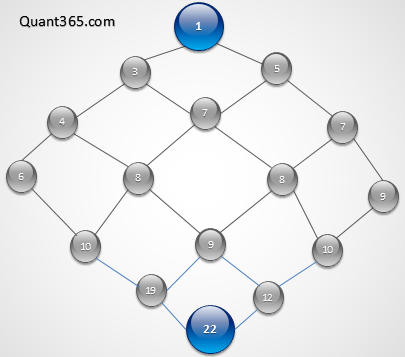
这个是上半截Young tableau的heap表示,注意相同色彩的点其实是一个点.
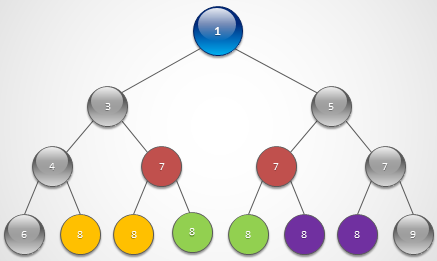
两个数据结构的特点都是父节点大于两个子节点而子节点之间没有必然大小关系! 此外Young Tableau的最底节点是最大节点,所以它不但有最小值还有最大值,包含的信息更加丰富. 而且,YT的上面两条边都比中间对应值要小,下面两条边比中间对应值大,所以它比heap更加有序.
Young Tableau是把两个heap的bottom/leaves对接,如果把两个heap的top/root对接,就成了求median/percentile的数据结构.
可见这几个数据结构是紧密联系的.
http://bookshadow.com/weblog/2016/08/01/leetcode-kth-smallest-element-in-a-sorted-matrix/
这个算法非常像从index heap里面找topK
首先将矩阵的左上角(下标0,0)元素加入堆,然后执行k次循环:
弹出堆顶元素top,记其下标为i, j
将其下方元素matrix[i + 1][j],与右方元素matrix[i][j + 1]加入堆(若它们没有加入过堆)
…
上述解法的优化:
实际上visited数组可以省去,在队列扩展时,当且仅当i == 0时才向右扩展,否则只做向下扩展.
T: \(O(K LogK)\)
struct Node {
int val, i, j;
Node(int i, int j, int val) :i(i), j(j), val(val) {}
bool operator<(const Node & x) const { return val > x.val; }
};
struct Solution {
int kthSmallest(vector<vector<int>>& matrix, int k) {
priority_queue<Node> q;
int n = matrix.size();
q.push(Node(0, 0, matrix[0][0]));
while (--k) {
Node x = q.top(); q.pop();
if (x.i == 0 && x.j + 1 < n)
q.push(Node(x.i, x.j + 1, matrix[x.i][x.j + 1]));
if (x.i + 1 < n)
q.push(Node(x.i + 1, x.j, matrix[x.i + 1][x.j]));
}
return q.top().val;
}
};注意这里priority_queue的用法,里面装的是Node,因为会用到operator<,但是我需要一个min heap,所以里面用自己的val大于输入值的val.
下图展示的是先把第一行加到heap里面,然后pop出的点只需要向下走就行了的算法.严格说来没有上面的代码时间复杂度优,但是写起来会更加简单.
T: \(O(min(N,K) + KLog max(N))\)
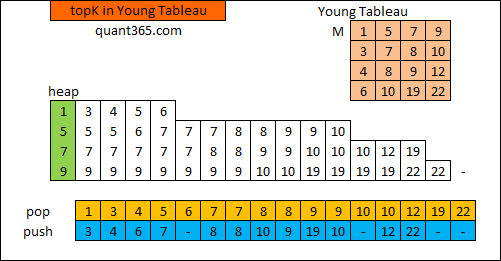
下面的博客采用的这种算法:
https://all4win78.wordpress.com/2016/08/01/leetcode-378-kth-smallest-element-in-a-sorted-matrix/
http://www.geeksforgeeks.org/kth-smallest-element-in-a-row-wise-and-column-wise-sorted-2d-array-set-1/
8.17.2.1 Algo 3: Improved Saddleback Search
https://discuss.leetcode.com/topic/53126/o-n-from-paper-yes-o-rows
8.18 668. Kth Smallest Number in Multiplication Table
Nearly every one have used the Multiplication Table. But could you find out the k-th smallest number quickly from the multiplication table?
Given the height m and the length n of a m * n Multiplication Table, and a positive integer k, you need to return the k-th smallest number in this table.
Example 1:
Input: m = 3, n = 3, k = 5
Output:
Explanation:
The Multiplication Table:
1 2 3
2 4 6
3 6 9
The 5-th smallest number is 3 (1, 2, 2, 3, 3).
Example 2:
Input: m = 2, n = 3, k = 6
Output:
Explanation:
The Multiplication Table:
1 2 3
2 4 6
The 6-th smallest number is 6 (1, 2, 2, 3, 4, 6).
https://leetcode.com/problems/kth-largest-number-in-multiplication-table the same as: http://codeforces.com/contest/448/problem/D
8.19 79. Word Search
Given a 2D board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.
For example,
Given board =
[
[‘A’,‘B’,‘C’,‘E’],
[‘S’,‘F’,‘C’,‘S’],
[‘A’,‘D’,‘E’,‘E’]
]
word = “ABCCED”, -> returns true,
word = “SEE”, -> returns true,
word = “ABCB”, -> returns false.
 https://leetcode.com/problems/word-search/
https://leetcode.com/problems/word-search/
8.19.1 DFS
- CPP
class Solution {
public:
vector<pair<int,int>> dirs={{1,0},{0,1},{-1,0},{0,-1}};
int R=0, C=0;
bool exist(vector<vector<char>>& b, string w) {
if(b.empty() || b[0].empty()) return w.empty();
R=b.size(), C=b[0].size();
vector<vector<bool>> m(R,vector<bool>(C));//visited
for(int i=0;i<R;i++){
for(int j=0;j<C;++j){
if (!m[i][j] && dfs(b,w,i,j,0,m))
return true;
}
}
return false;
}
bool dfs(vector<vector<char>>& b, string& w,
int i, int j, int h, vector<vector<bool>> m)
{
if(b[i][j]!=w[h]) return false;
m[i][j] = true;
for(auto pr: dirs){
int nx=i+pr.first, ny=j+pr.second;
if(nx<0 or nx==R or ny<0 or ny==C) continue;//boundry
if(!m[nx][ny] && dfs(b,w,nx,ny,h+1,m))
return true;
}
return h==w.size()-1; // [[a]], ab, a
}
};- Java
public class Solution {
public boolean exist(char[][] board, String word) {
if(board == null || board.length == 0 ||
board[0] ==null || board[0].length == 0) {
return false;
}
if(word == null || word.length() == 0) {
return true;
}
int m = board.length;
int n = board[0].length;
boolean[][] visited = new boolean[m][n];
char[] words = word.toCharArray();//
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
boolean exist = dfs(board,i,j,words,0,visited);
if(exist) {
return true;
}
}
}
return false;
}
public boolean dfs(char[][] board, int row, int col,
char[] words,int pos, boolean[][] visited)
{
if(pos == words.length){
return true;
}
if(row<0 || row >=board.length || col < 0 || col >= board[0].length) {
return false;
}
if(visited[row][col]) {
return false;
}
if(board[row][col] != words[pos]){
return false;
}
visited[row][col] = true;
boolean exist= dfs(board,row-1,col,words,pos+1,visited)
|| dfs(board,row+1,col,words,pos+1,visited)
|| dfs(board,row,col-1, words,pos+1,visited)
|| dfs(board,row,col+1,words,pos+1,visited);
visited[row][col] = false; //
return exist;
}
}8.20 Word Search II
Given a 2D board and a list of words from the dictionary, find all words in the board.
Each word must be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
For example,
Given words = [“oath”,“pea”,“eat”,“rain”] and board =
[
['o','a','a','n'],
['e','t','a','e'],
['i','h','k','r'],
['i','f','l','v']
]Return [“eat”,“oath”]. Note: You may assume that all inputs are consist of lowercase letters a-z.
 https://leetcode.com/problems/word-search-ii/
https://leetcode.com/problems/word-search-ii/
http://www.cnblogs.com/grandyang/p/4516013.html
http://www.cnblogs.com/easonliu/p/4514110.html
http://blog.csdn.net/ljiabin/article/details/45846527
https://discuss.leetcode.com/topic/14307/27-lines-uses-complex-numbers/3
http://massivealgorithms.blogspot.com/2015/05/leetcode-q212-word-search-ii-lei-jiang.html > Naive(Graph DFS + Bitmap)
(Letter) Trie + Graph DFS + Bitmap + Pruning
Time comeplexity
Let’s think about the naive solution first. The naive solution is we search the board for each board. So for the dict with \(N\) words, and assume the ave. length of each word has length of \(L\). Then without using a Trie, the time complexity would be \(O(N * R * C * 4^L)\).
Now let’s analyze the time complexity of using a Trie. We put each word into the trie. Search in the Trie takes O(m) time, so the time complexity would be O(rows * cols * m * 4^m). Since mostly m << n, using a trie would save lots of time.
Key points:
- bitmap can be saved if you mark the visited cell as some invalid char like ‘#’, and recover it after dfs call.
- Trie can remove dups:
You do not need Set<String> res to remove duplicate.
You could just use List<String> res.
Because the Trie has the ability of remove duplicate.
All you need to do is to change
if(p.word != null) res.add(p.word);
Into
if(p.word != null) {
res.add(p.word);
p.word = null;
}Which removes the found word from the Trie. And you can just return res itself.
https://discuss.leetcode.com/topic/33246/java-15ms-easiest-solution-100-00/8
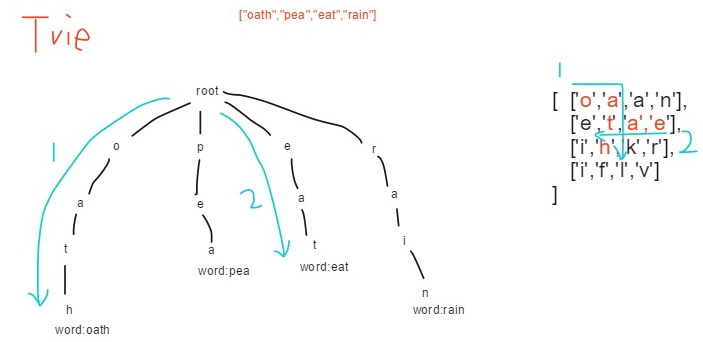
8.21 Extension topics
- Extension to higher space, say 3D array(cube).
vector<vector<vector<int>>> _3darray;8.22 73. Set Matrix Zeroes
 https://leetcode.com/problems/set-matrix-zeroes/
https://leetcode.com/problems/set-matrix-zeroes/
http://www.cnblogs.com/lichen782/p/leetcode_Set_Matrtix_Zero.html
Requires \(O(1)\) space!
Not difficult algorithm, but very error prone for implementation.
这是一个矩阵操作的题目,目标很明确,就是如果矩阵如果有元素为0,就把对应的行和列上面的元素都置为0.这里最大的问题就是我们遇到0的时候不能直接把矩阵的行列在当前矩阵直接置0,否则后面还没访问到的会被当成原来是0,最后会把很多不该置0的行列都置0了.
一个直接的想法是备份一个矩阵,然后在备份矩阵上判断,在原矩阵上置0,这样当然是可以的,不过空间复杂度是\(O(m*n)\),不是很理想.
上面的方法如何优化呢?我们看到其实判断某一项是不是0只要看它对应的行或者列应不应该置0就可以,所以我们可以维护一个行和列的布尔数组,然后扫描一遍矩阵记录那一行或者列是不是应该置0即可,后面赋值是一个常量时间的判断.这种方法的空间复杂度是\(O(m+n)\).
其实还可以再优化,我们考虑使用第一行和第一列来记录上面所说的行和列的置0情况,这里问题是那么第一行和第一列自己怎么办?想要记录它们自己是否要置0,只需要两个变量(一个是第一行,一个是第一列)就可以了.然后就是第一行和第一列,如果要置0,就把它的值赋成0(反正它最终也该是0,无论第一行或者第一列有没有0),否则保留原值.然后根据第一行和第一列的记录对其他元素进行置0.最后再根据前面的两个标记来确定是不是要把第一行和第一列置0就可以了.这样的做法只需要两个额外变量,所以空间复杂度是\(O(1)\).
时间上来说上面三种方法都是一样的,需要进行两次扫描,一次确定行列置0情况,一次对矩阵进行实际的置0操作,所以总的时间复杂度是\(O(m*n)\).
struct Solution {
void setZeroes(vector<vector<int>>& m) {
if(m.empty()) return;
const int target=0, marker=0; //generalization
int R=m.size(), C=m[0].size();
bool row0 =false, col0=false;
for(int i=0;i<C;++i) if(m[0][i]==target){ row0=true; break; }
for(int i=0;i<R;++i) if(m[i][0]==target){ col0=true; break; }
for(int i=1;i<R;++i)
for(int j=1;j<C;++j)
if((m[i][0]!=marker || m[0][j]!=marker) && m[i][j]==target)
m[i][0]=marker, m[0][j]=marker;
for(int i=1; i<R; ++i)
for(int j=1; j<C; ++j)
if(m[i][0]==marker||m[0][j]==marker) m[i][j]=marker;
if(row0) for(int i=0;i<C;++i) m[0][i]=marker;
if(col0) for(int i=0;i<R;++i) m[i][0]=marker;
}
};Corner case:
{{1,0}}, {{0},{1}}, {}Follow up:
- How about set diagonal/antidiagonal cells to marker?
8.23 Union-Find(Number of Islands)
 https://leetcode.com/problems/number-of-islands/
https://leetcode.com/problems/number-of-islands/
#include <numeric>
struct Solution {
vector<int> bo;
vector<int> sz;
void makeset(int len) { // everybody is his/her own boss.
bo.resize(len);
iota(bo.begin(), bo.end(), 0);
sz.resize(len);
fill(sz.begin(), sz.end(), 1);
}
int findset(int x) { // find boss
if (x != bo[x]) bo[x] = findset(bo[x]); //// Be careful it is `if`
return bo[x];
};
void merge(int x, int y) {
int bo1 = findset(x), bo2 = findset(y);// after this line, no x and y any more!!
if (bo1 == bo2) return;
int sma = sz[bo1] > sz[bo2] ? bo2 : bo1;
int big = sz[bo1] > sz[bo2] ? bo1 : bo2;
bo[sma] = big, sz[big] += sz[sma], sz[sma] = 0;
/*if (sz[bo1] > sz[bo2]) bo[bo2] = bo1, sz[bo1] += sz[bo2], sz[bo2] = 0;
else bo[bo1] = bo2, sz[bo2] += sz[bo1], sz[bo1] = 0;
*/
};
int numIslands(vector<vector<bool>>& grid) {
if (grid.empty() || grid[0].empty()) return 0;
const vector<pair<int, int>> DIR = {{ 0, -1 },{ -1,0 },{ 1,0 },{ 0,1 }};
const int R = grid.size(), C = grid[0].size();
makeset(R*C);
auto m2a = [C](int x, int y) {return x*C + y; };////
for (int i = 0; i<R; ++i) {
for (int j = 0; j<C; ++j) {
int aidx = m2a(i, j);//array index
if (!grid[i][j]) {
sz[aidx] = 0;
continue;
}
for (auto d : DIR) {
int ni = i + d.first, nj = j + d.second;
int naidx = m2a(ni, nj);
if (ni >= 0 && ni<R && nj >= 0 && nj<C && grid[ni][nj]/* && aidx<naidx*/)
merge(aidx, naidx);
}
}
}
return count_if(sz.cbegin(), sz.cend(), [](int i) {return i>0; });
}
};Another way to make set:
8.24 305. Number of Islands II
A 2d grid map of m rows and n columns is initially filled with water. We may perform an addLand operation which turns the water at position (row, col) into a land. Given a list of positions to operate, count the number of islands after each addLand operation. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example:
Given m = 3, n = 3, positions = [[0,0], [0,1], [1,2], [2,1]].
We return the result as an array: [1, 1, 2, 3]
https://leetcode.com/problems/number-of-islands-ii
这道题只能用union find了现在. No more DFS.
class Solution {
public:
vector<int> numIslands2(int m, int n, vector<pair<int, int>>& positions) {
vector<int> res;
roots = vector<int>(m * n, -1);
vector<pair<int, int>> dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
int island = 0;
for (auto pos : positions) {
int x = pos.first, y = pos.second, idx_p = x * n + y;
roots[idx_p] = idx_p;
++island;
for (auto dir : dirs) {
int row = x + dir.first, col = y + dir.second, idx_new = row * n + col;
if (row >= 0 && row < m && col >= 0 && col < n && roots[idx_new] != -1) {
int rootNew = findRoot(idx_new), rootPos = findRoot(idx_p);
if (rootPos != rootNew)
roots[rootPos] = rootNew, --island;
}
}
res.push_back(island);
}
return res;
}
private:
vector<int> roots;
int findRoot(int idx) {
if(idx != roots[idx]) roots[idx]=findRoot(roots[idx]);
return roots[idx];
}
};8.24.1 Number of Distinct Islands
 有多少个形状不同的岛
有多少个形状不同的岛
There are two same shape islands(black and brown ones) in the picture above. The purple one doesn’t count.
http://bit.ly/2woGNgP, http://bit.ly/2wpgCXh
这个Follow up是经典 number of distinct islands. 比之前的明显要难些. 需要用到hashing得思想.每一个岛将遍历完的点id(每个cell 可以分配一个id, id = i*m+j) 组合起来, 返回字符串,比如 “1/2/3/5” 这个岛有四个点. 如果另一个岛是 “11/12/13/15” 只要把它offset下, 第一位归1, 它也变成“1/2/3/5”, 所以这2个岛的shape是一样的. 将这些第一位归1的字符串往set里丢.自然就除重了.
中心思想: 将CELL ID组合来表示一个岛(hash to string),然后变形string, 最后往set里丢. done
8.25 422. Valid Word Square
 https://leetcode.com/problems/valid-word-square/
https://leetcode.com/problems/valid-word-square/
http://www.cnblogs.com/grandyang/p/5991673.html
bool validWordSquare(vector<string>& w) {
for(int i=0;i<w.size();i++)
for(int j=0;j<w[i].size();j++)
if(j>=w.size() || i>=w[j].size() || w[i][j] != w[j][i]) return false;
return true;
}Symetric Irregular Matrix - Key point is the boundary condition check. Also examplify the index based loop is required here than auto loop.
8.26 425. Word Squares
Given a set of words (without duplicates), find all word squares you can build from them.
A sequence of words forms a valid word square if the kth row and column read the exact same string, where 0 ≤ k < max(numRows, numColumns).
For example, the word sequence [“ball”,“area”,“lead”,“lady”] forms a word square because each word reads the same both horizontally and vertically.
b a l l
a r e a
l e a d
l a d yNote:
There are at least 1 and at most 1000 words.
All words will have the exact same length.
Word length is at least 1 and at most 5.
Each word contains only lowercase English alphabet a-z.Example:
Input:
["area","lead","wall","lady","ball"]
Output:
[
[ "wall",
"area",
"lead",
"lady"
],
[ "ball",
"area",
"lead",
"lady"
]
]Explanation: The output consists of two word squares. The order of output does not matter (just the order of words in each word square matters).
 https://leetcode.com/problems/word-squares/
https://leetcode.com/problems/word-squares/
这个题目有个隐含条件没有明说,就是word可以重复使用.

一看这是一个对称矩阵.填充的方式比较怪,从左上角到右下角,而且一次填充同时填充行和列(因此矩阵是对称的).填充的“材料”必须从给定的字符串序列中选取.选取的依据是Prefix matching.从这一点上立刻想到用trie.因为是单纯的需要一个prefix matching功能,unordered_map也可以完成这个任务,而且有STL内置函数支持,所以编码会很方便.因为每一步填充的时候有多种选择,好似在Graph中走路有多个路口一样,而且要求返回所有的行进可能,所以自然想到要用DFS. 于是就有了下面第一种方法:
Solution 1 - DFS + unordered_map:
struct Solution { // 25 lines, 252 ms
int n;
unordered_map<string, vector<string>> trie;
vector<string> square;
vector<vector<string>> squares;
vector<vector<string>> wordSquares(vector<string>& words) {
n = words[0].size();
square.resize(n);
for (string& word : words)
for (int i = 0; i<n; i++)
trie[word.substr(0, i)].push_back(word);
dfs(0);
return squares;
}
void dfs(int i) {
if (i == n) {
squares.push_back(square);
return;
}
string prefix;
for (int k = 0; k<i; k++) prefix += square[k][i];
for (string& word : trie[prefix])
square[i] = word, dfs(i + 1);
}
};如果坚持要用Trie来实现,可以用implement-trie-prefix-tree的方法建一个trie,并实现get_words_start_with方法.
Solution 2 - DFS + Trie:
#define ix(x) (x-'a')
struct node {
bool k = false;// k represent the end of a string
node *n[26] = {};// Use index to represent the current char, n mean next
};
struct trie {
trie() { r = new node(); }
void insert(const string& s) {
node* cur = r;
for (char c : s) {
if (cur->n[ix(c)] == 0) cur->n[ix(c)] = new node();
cur = cur->n[ix(c)];
}
cur->k = true;
}
vector<string> get_words_start_with(const string& s) {
vector<string> re;
node* cur = r;
for (char c : s) {
if (cur == 0 || cur->n[ix(c)] == 0) return re;
cur = cur->n[ix(c)];
}
_getwords(cur, re, s);
return re;
}
private:
void _getwords(node* no, vector<string>& re, const string& prefix) {
if (no->k) re.push_back(prefix);
for (int i = 0; i<26; i++)
if (no->n[i]) _getwords(no->n[i], re, prefix + (char)('a' + i));
}
node* r; // root
};
struct Solution { //359 ms
vector<vector<string>> wordSquares(vector<string>& words) {
trie tr;
for_each(words.begin(), words.end(), [&tr](const string& s) {tr.insert(s); });
vector<vector<string>> r;
vector<string> p;
for (string& s : words) dfs(r, p, s, &tr, 1);
return r;
}
string get_prefix(const vector<string>& vs, int i) {
string r;
for (const string& s : vs) r += s[i];
return r;
}
void dfs(vector<vector<string>>& r, vector<string>& p, string& s, trie* ptr, int start) {
p.push_back(s);
if (start >= s.size())
r.push_back(p);
else {
vector<string> t = ptr->get_words_start_with(get_prefix(p, start));
for (string& ns : t) dfs(r, p, ns, ptr, start + 1);
}
p.pop_back();
}
};上面的trie方法速度比较慢,空间占用也大,下面的方法做了一些改进:
- 在每一个节点记录对应的单词. 因为这个trie在本题的目的就是prefix matching查询, 所以这样的话可以提高效率, match完prefix之后立即返回值,不需要继续搜索到树的叶节点.注意这里还用了
const char*而非string,也是为了优化的缘故. - 用vector存放整个trie树,可以更好的利用CPU cache.原来的方法是用指针来连接父子节点,现在是用vector index.
Solution 2 - DFS + Trie(Optimized):
struct Solution { // 75ms, 90%
struct TrieNode {
vector<const char*> words; //avoid using string for optimization
int nodes[26] = {};
};
vector<vector<string>> wordSquares(vector<string>& words) {
//1. Build trie
vector<TrieNode> trie(1); // 0 as root node
for (const auto& s : words) {
int i = 0;
for (char ch : s) {
if (trie[i].nodes[ch - 'a'] == 0) {
trie[i].nodes[ch - 'a'] = trie.size();
trie.push_back(TrieNode());
}
i = trie[i].nodes[ch - 'a'];
trie[i].words.push_back(s.c_str());
}
}
//2. DFS
vector<vector<string>> r;
vector<string> p;
for (string& s : words) dfs(r, p, trie, s.c_str(), 1);
return r;
}
void dfs(vector<vector<string>>& r, vector<string>& p, vector<TrieNode>& trie, const char* s, int k) {
p.push_back(s);
if (k == strlen(s)) {
r.push_back(p);
} else {
int i = 0;
for (string& ns : p)
if ((i = trie[i].nodes[ns[k] - 'a']) == 0) break;
if (i>0) for (const char* ns : trie[i].words) dfs(r, p, trie, ns, k + 1);
}
p.pop_back();
}
};注意在prefix matching的时候,当trie vector index i变为0的时候,说明下面没有节点了,match失败.
Follow up:
- match之后需要删除word吗? 如果word可以重复使用的话,{“baba”,“amat”,“apam”}三个string就可以构成一个word square.
baba
apam
baba
amat否则就不可以.
从trie删除word, Solution 2非常方便. Solution 1和3都不方便,因为存了word在很多不同的地方,需要逐一找到并删除.
- Word长度不相同怎么办?
注意根据422. Valid Word Square, 这个是valid word square:
abcd
bnrt
crm
dt这个不是:
papa
amazon
papa
azan
o
n8.27 361. Bomb Enemy
 https://leetcode.com/problems/bomb-enemy/
https://leetcode.com/problems/bomb-enemy/
brute force的话T: \(O(R*C*(R+C))\)
开始想可否每边用一个array共4个array来解决,但是如果一行有多个wall的话就不行.
后来分析了下可以用4次扫描并累加的方式.需要用\(O(R*C)\)空间复杂度.
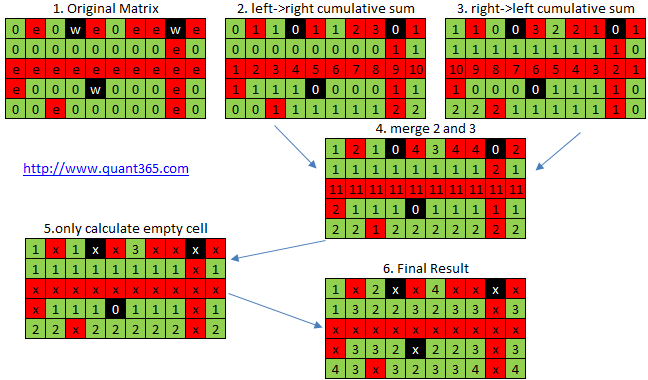
int maxKilledEnemies(vector<vector<char>>& g) { //T/S: O(R*C)
if (g.empty() || g[0].empty()) return 0;//
int R = g.size(), C= g[0].size(); //
vector<vector<int>> c(R,vector<int>(C,0));//counter matrix
int r=0, tmp=0, i=0, j=0;
auto f=[&](int i, int j){
if('0'==g[i][j]){c[i][j]+=tmp, r=max(r,c[i][j]);}else if('W'==g[i][j]){tmp=0;}else{tmp++;}
};
for(i=0;i<R;i++) for(j=tmp=0;j<C;j++) f(i,j);
for(i=0;i<R;i++) for(j=C-1,tmp=0;j>=0;j--) f(i,j);
for(j=0;j<C;j++) for(i=tmp=0;i<R;i++) f(i,j);
for(j=0;j<C;j++) for(i=R-1,tmp=0;i>=0;i--) f(i,j);
return r;
}Walk through the matrix. At the start of each non-wall-streak (row-wise or column-wise), count the number of hits in that streak and remember it. O(mn) time, O(n) space.
int maxKilledEnemies(vector<vector<char>>& grid) {
int m = grid.size(), n = m ? grid[0].size() : 0;
int result = 0, rowhits, colhits[n];
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if (!j || grid[i][j-1] == 'W') {
rowhits = 0;
for (int k=j; k<n && grid[i][k] != 'W'; k++)
rowhits += grid[i][k] == 'E';
}
if (!i || grid[i-1][j] == 'W') {
colhits[j] = 0;
for (int k=i; k<m && grid[k][j] != 'W'; k++)
colhits[j] += grid[k][j] == 'E';
}
if (grid[i][j] == '0')
result = max(result, rowhits + colhits[j]);
}
}
return result;
}8.28 419. Battleships in a Board
Given an 2D board, count how many battleships are in it. The battleships are represented with ‘X’s, empty slots are represented with’.’s. You may assume the following rules:
You receive a valid board, made of only battleships or empty slots.
Battleships can only be placed horizontally or vertically. In other words, they can only be made of the shape 1xN (1 row, N columns) or Nx1 (N rows, 1 column), where N can be of any size.
At least one horizontal or vertical cell separates between two battleships - there are no adjacent battleships.
Example:
X..X
...X
...XIn the above board there are 2 battleships.
Invalid Example:
...X
XXXX
...XThis is an invalid board that you will not receive - as battleships will always have a cell separating between them.
Follow up: Could you do it in one-pass, using only O(1) extra memory and without modifying the value of the board?
https://leetcode.com/problems/battleships-in-a-board/
count how many battleships are in it.
http://bookshadow.com/weblog/2016/10/13/leetcode-battleships-in-a-board/
http://www.cnblogs.com/grandyang/p/5979207.html
class Solution {
public:
int countBattleships(vector<vector<char>>& board) {
if (board.empty() || board[0].empty()) return 0;
int res = 0, m = board.size(), n = board[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (board[i][j] == '.' || // 戰艦頭
(i > 0 && board[i - 1][j] == 'X') ||
(j > 0 && board[i][j - 1] == 'X')) continue;
++res;
}
}
return res;
}
};8.29 531. Lonely Pixel I
Given a picture consisting of black and white pixels, find the number of black lonely pixels.
The picture is represented by a 2D char array consisting of ‘B’ and ‘W’, which means black and white pixels respectively.
A black lonely pixel is character ‘B’ that located at a specific position where the same row and same column don’t have any other black pixels.
Example:
Input:
[['W', 'W', 'B'],
['W', 'B', 'W'],
['B', 'W', 'W']]
Output: 3
Explanation: All the three 'B's are black lonely pixels.8.29.1 Algo 1
T: \(O(MN)\) S: \(O(M+N)\)
struct Solution { // 50%
int findLonelyPixel(vector<vector<char>>& pic) {
int m = pic.size(), n = pic[0].size();
vector<int> rows(m), cols(n);
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
rows[i] += pic[i][j] == 'B', cols[j] += pic[i][j] == 'B';
int lonely = 0;
for (int i = 0; i < m; i++)
for (int j = 0; j < n && rows[i]; j++)
lonely += pic[i][j] == 'B' && rows[i] == 1 && cols[j] == 1;
return lonely;
}
};8.29.2 Algo 2
T: \(\Theta(MN)\) S: \(O(M)\)
struct Solution { // 58%
int findLonelyPixel(vector<vector<char>>& picture) {
int R=picture.size(), C=picture[0].size();
vector<bool> rv(R);
int i=0, r=0;
generate(rv.begin(), rv.end(), [&](){ // O(MN)
int k=0, j=C;
while(j-- && k<2) picture[i][j]=='B' && k++;
i++; return k==1;});
for(int c=0;c<C;++c){ // O(MN)
bool k=false;
for(int w=0;w<R;++w)
if(picture[w][c]!='B') continue;
else if(!rv[w]) break;
else if(!k && rv[w]) k=true;
else if(k){k=false; break;}
k && ++r;
}
return r;
}
};8.30 533. Lonely Pixel II
Given a picture consisting of black and white pixels, and a positive integer N, find the number of black pixels located at some specific row R and column C that align with all the following rules:
1. Row R and column C both contain exactly N black pixels.
2. For all rows that have a black pixel at column C, they should be exactly the same as row RThe picture is represented by a 2D char array consisting of ‘B’ and ‘W’, which means black and white pixels respectively.
Example:
Input:
[['W', 'B', 'W', 'B', 'B', 'W'],
['W', 'B', 'W', 'B', 'B', 'W'],
['W', 'B', 'W', 'B', 'B', 'W'],
['W', 'W', 'B', 'W', 'B', 'W']] N = 3
Output: 6
Explanation: All the bold ‘B’ are the black pixels we need (all ’B’s at column 1 and 3).
0 1 2 3 4 5 column index
0 [['W', 'B', 'W', 'B', 'B', 'W'],
1 ['W', 'B', 'W', 'B', 'B', 'W'],
2 ['W', 'B', 'W', 'B', 'B', 'W'],
3 ['W', 'W', 'B', 'W', 'B', 'W']]
row indexTake ‘B’ at row R = 0 and column C = 1 as an example:
Rule 1, row R = 0 and column C = 1 both have exactly N = 3 black pixels.
Rule 2, the rows have black pixel at column C = 1 are row 0, row 1 and row 2. They are exactly the same as row R = 0.
https://leetcode.com/problems/lonely-pixel-ii/
注意第二个条件是说所有的满足条件的行要相同.由于多了这个条件,我们引入了一个map解题.
struct Solution {
int findBlackPixel(vector<vector<char>>& picture, int N) {
int R=picture.size(), C=picture[0].size(), r=0;
vector<int> rv(R), cv(C);
for(int i=0;i<R;++i)
for(int j=0;j<C;++j)
if(picture[i][j]=='B') rv[i]++, cv[j]++;
unordered_map<string, int> m;//string to counter
for(int i=0;i<R;++i){
string t;
for(int j=0;j<C;++j) t+=picture[i][j];
m[t]++;
}
for(int i=0;i<R;++i){
string t;
for(int k=0;k<C;++k) t+=picture[i][k];
for(int j=0;j<C;++j)
if(picture[i][j]=='B' && rv[i]==N && cv[j]==N && m[t]==N) r++;
}
return r;
}
};8.31 624. Maximum Distance in Arrays
Given m arrays, and each array is sorted in ascending order. Now you can pick up two integers from two different arrays (each array picks one) and calculate the distance. We define the distance between two integers a and b to be their absolute difference |a-b|. Your task is to find the maximum distance.
Example 1:
Input:
[[1,2,3],
[4,5],
[1,2,3]]
Output: 4Explanation:
One way to reach the maximum distance 4 is to pick 1 in the first or third array and pick 5 in the second array.
8.32 661. Image Smoother
Given a 2D integer matrix M representing the gray scale of an image, you need to design a smoother to make the gray scale of each cell becomes the average gray scale (rounding down) of all the 8 surrounding cells and itself. If a cell has less than 8 surrounding cells, then use as many as you can.
Example 1:
Input:
[[1,1,1],
[1,0,1],
[1,1,1]]
Output:
[[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]Explanation:
For the point (0,0), (0,2), (2,0), (2,2): floor(3/4) = floor(0.75) = 0
For the point (0,1), (1,0), (1,2), (2,1): floor(5/6) = floor(0.83333333) = 0
For the point (1,1): floor(8/9) = floor(0.88888889) = 0
例如原始矩阵是这样的:
a b c d
e f g h
i j k l
m n o p然后先跑一轮,将矩阵变成
a+e b+f c+g d+h
a+e+i b+f+j c+g+k d+h+l
e+i+m f+j+n g+k+o h+l+p
i+m j+n k+o l+p如此,每个cell的结果就是只跟本行cell值相关,与上下行cell无关了.
https://leetcode.com/problems/image-smoother
http://bit.ly/2x2heSW
T: \((R*C)\), ES: \(O(1)\) 这道题的Constant Space解法如下:
struct Solution { // Your runtime beats 98.78 % of cpp submissions.
vector<vector<int>> imageSmoother(vector<vector<int>>& M) {
if(M.empty() || M[0].empty()) return {};
int R=M.size(), C=M[0].size();
for(int j=0;j<C;++j)
for(int i=0,p=0,t=0;i<R;++i)
t=M[i][j], M[i][j]+=p+((i+1<R)?M[i+1][j]:0), p=t;
for(int i=0;i<R;++i)
for(int j=0,p=0,t=0;j<C;++j)
t=M[i][j], M[i][j]+=p+((j+1<C)?M[i][j+1]:0), p=t;
for(int i=0;i<R;++i)
for(int j=0;j<C;++j)
if ((i==0&&(j==0||j==C-1))||(i==R-1&&(j==0||j==C-1))) M[i][j]/=min(2,R)*min(2,C);
else if(i==0||i==R-1) M[i][j]/=min(R,2)*3;
else if(j==0||j==C-1) M[i][j]/=min(C,2)*3;
else M[i][j] /= 9;
return M;
}
};8.33 542. 01 Matrix
Given a matrix consists of 0 and 1, find the distance of the nearest 0 for each cell. The distance between two adjacent cells is 1.
Example 1:
Input:
0 0 0
0 1 0
0 0 0
Output:
0 0 0
0 1 0
0 0 0
Example 2:
Input:
0 0 0
0 1 0
1 1 1
Output:
0 0 0
0 1 0
1 2 1https://leetcode.com/problems/01-matrix
http://www.cnblogs.com/grandyang/p/6602288.html
我们可以首先遍历一次矩阵,将值为0的点都存入queue,将值为1的点改为INT_MAX.之前像什么遍历迷宫啊,起点只有一个,而这道题所有为0的点都是起点,这想法,叼!然后开始BFS遍历,从queue中取出一个数字,遍历其周围四个点,如果越界或者周围点的值小于等于当前值,则直接跳过.因为周围点的距离更小的话,就没有更新的必要,否则将周围点的值更新为当前值加1,然后把周围点的坐标加入queue,参见代码如下:
struct Solution {
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> dirs{{0,-1},{-1,0},{0,1},{1,0}};
queue<pair<int, int>> q;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (matrix[i][j] == 0) q.push({i, j}); else matrix[i][j] = INT_MAX;
while (!q.empty()) {
auto t = q.front(); q.pop();
for (auto dir : dirs) {
int x = t.first + dir[0], y = t.second + dir[1];
if (x < 0 || x >= m || y < 0 || y >= n ||
matrix[x][y] <= matrix[t.first][t.second]) continue;
matrix[x][y] = matrix[t.first][t.second] + 1;
q.push({x, y});
}
}
return matrix;
}
};8.34 Longest Increasing Path in a Matrix
Given an integer matrix, find the length of the longest increasing path.
From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).
Example 1: ~~~~~~ nums = [ [*9,9,4], [*6,6,8], [2,1,1]] ~~~~~~ Return 4
The longest increasing path is [1, 2, 6, 9].
Example 2: ~~~~~~ nums = [ [3,4,*5], [3,2,*6], [2,2,1]] ~~~~~~ Return 4
The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.
 https://leetcode.com/problems/longest-increasing-path-in-a-matrix/
https://leetcode.com/problems/longest-increasing-path-in-a-matrix/
T:\(O(R*C)\), S:\(O(R*C)\)
Tag: DFS, Memorization, Google
struct Solution {// 69 ms, Your runtime beats 56.04% of cpp submissions.
int R, C;
int longestIncreasingPath(vector<vector<int>>& matrix) {
if(matrix.empty() or matrix[0].empty()) return 0;
R=matrix.size(), C=matrix[0].size();
vector<vector<int>> c(R,vector<int>(C));
int r=INT_MIN;
for(int i=0;i<R;++i){
for(int j=0;j<C;++j){
dfs(c,matrix,i,j);
r = max(r, c[i][j]);
}
}
return r;
}
vector<pair<int,int>> dirs={{-1,0},{1,0},{0,1},{0,-1}};
void dfs(vector<vector<int>>& c, vector<vector<int>>& matrix, int i, int j){
if (c[i][j]) return;
for(auto p: dirs){
int ni=i+p.first, nj=j+p.second;
if (ni>=0 and ni<R and nj>=0 and nj<C){
if(matrix[i][j]<matrix[ni][nj]){
if (!c[ni][nj])
dfs(c,matrix,ni,nj);
c[i][j]=max(1+c[ni][nj], c[i][j]);
}
}
}
if(!c[i][j]) c[i][j]=1;
}
};Time complexity of the above solution is \(O(R*C)\). It may seem more at first look. If we take a closer look, we can notice that all values of c[i][j] are computed only once.
Refer:
http://bookshadow.com/weblog/2016/01/20/leetcode-longest-increasing-path-matrix/
http://www.lintcode.com/en/problem/longest-increasing-subsequence/
http://www.voidcn.com/blog/qq_20480611/article/p-6140833.html
http://www.geeksforgeeks.org/find-the-longest-path-in-a-matrix-with-given-constraints
8.35 675. Cut Off Trees for Golf Event
You are asked to cut off trees in a forest for a golf event. The forest is represented as a non-negative 2D map, in this map:
- 0 represents the obstacle can’t be reached.
- 1 represents the ground can be walked through.
- The place with number bigger than 1 represents a tree can be walked through, and this positive number represents the tree’s height.
You are asked to cut off all the trees in this forest in the order of tree’s height - always cut off the tree with lowest height first. And after cutting, the original place has the tree will become a grass (value 1).
You will start from the point (0, 0) and you should output the minimum steps you need to walk to cut off all the trees. If you can’t cut off all the trees, output -1 in that situation.
You are guaranteed that no two trees have the same height and there is at least one tree needs to be cut off.
Example 1:
Input:
[
[1,2,3],
[0,0,4],
[7,6,5]
]
Output: 6
Example 2:
Input:
[
[1,2,3],
[0,0,0],
[7,6,5]
]
Output: -1
Example 3:
Input:
[
[2,3,4],
[0,0,5],
[8,7,6]
]
Output: 6Explanation: You started from the point (0,0) and you can cut off the tree in (0,0) directly without walking.
Hint: size of the given matrix will not exceed 50x50.
https://leetcode.com/problems/cut-off-trees-for-golf-event
http://zxi.mytechroad.com/blog/searching/leetcode-675-cut-off-trees-for-golf-event/
竞赛当日No1的解法:
int neigh[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int d[51][51][51][51];
class Solution {
public:
int cutOffTree(vector<vector<int> >& forest) {
vector<pair<int,pair<int,int> > > a;
int i,j,k,m,n,ans,x,y,z,l;
vector<pair<int,int> > q;
m=forest.size();
n=forest[0].size();
memset(d,-1,sizeof(d));
for (i=0;i<m;i++)
for (j=0;j<n;j++)
{
if (forest[i][j]>=2)
a.push_back(make_pair(forest[i][j],make_pair(i,j)));
if (forest[i][j]==0) continue;
q.clear();
q.push_back(make_pair(i,j));
d[i][j][i][j]=0;
for (k=0;k<q.size();k++)
{
z=d[i][j][q[k].first][q[k].second];
for (l=0;l<4;l++)
{
x=q[k].first+neigh[l][0];
y=q[k].second+neigh[l][1];
if ((x>=0)&&(x<m)&&(y>=0)&&(y<n)&&(forest[x][y]!=0)&&(d[i][j][x][y]==-1)){
d[i][j][x][y]=z+1;
q.push_back(make_pair(x,y));
}
}
}
}
a.push_back(make_pair(0,make_pair(0,0)));
sort(a.begin(),a.end());
ans=0;
for (i=0;i+1<a.size();i++){
if (d[a[i].second.first][a[i].second.second][a[i+1].second.first][a[i+1].second.second]==-1) return -1;
ans+=d[a[i].second.first][a[i].second.second][a[i+1].second.first][a[i+1].second.second];
}
return ans;
}
};No2的解法:
#include <bits/stdc++.h>
#define SZ(X) ((int)(X).size())
#define ALL(X) (X).begin(), (X).end()
#define REP(I, N) for (int I = 0; I < (N); ++I)
#define REPP(I, A, B) for (int I = (A); I < (B); ++I)
#define RI(X) scanf("%d", &(X))
#define RII(X, Y) scanf("%d%d", &(X), &(Y))
#define RIII(X, Y, Z) scanf("%d%d%d", &(X), &(Y), &(Z))
#define DRI(X) int (X); scanf("%d", &X)
#define DRII(X, Y) int X, Y; scanf("%d%d", &X, &Y)
#define DRIII(X, Y, Z) int X, Y, Z; scanf("%d%d%d", &X, &Y, &Z)
#define RS(X) scanf("%s", (X))
#define CASET int ___T, case_n = 1; scanf("%d ", &___T); while (___T-- > 0)
#define MP make_pair
#define PB push_back
#define MS0(X) memset((X), 0, sizeof((X)))
#define MS1(X) memset((X), -1, sizeof((X)))
#define LEN(X) strlen(X)
#define PII pair<int,int>
#define VI vector<int>
#define VL vector<long long>
#define VPII vector<pair<int,int> >
#define PLL pair<long long,long long>
#define VPLL vector<pair<long long,long long> >
#define F first
#define S second
typedef long long LL;
using namespace std;
const int MOD = 1e9+7;
const int SIZE = 1e6+10;
const LL INF = 1e18; //INF should be enough large.
typedef long long MYTYPE;
struct data{
MYTYPE v;
int id;
data(MYTYPE _v,int _id):v(_v),id(_id){}
bool operator<(const data& b)const{return v>b.v;}
};
struct Dijkstra{
vector<pair<int,MYTYPE> >e[SIZE];
MYTYPE mi[SIZE];
bool used[SIZE];
int n,tt;
void init(int _n){
n=_n;
REP(i,n+1)e[i].clear();
}
void add_edge(int x,int y,MYTYPE v){
e[x].PB(MP(y,v));
}
MYTYPE dis(int st,int ed){
priority_queue<data> qq;
REP(i,n+1)mi[i]=INF,used[i]=0;
mi[st]=0;
qq.push(data(0,st));
while(!qq.empty()){
data now=qq.top();qq.pop();
if(used[now.id])continue;
if(now.id==ed)return mi[ed];
used[now.id]=1;
REP(i,SZ(e[now.id])){
int y=e[now.id][i].F;
if(mi[y]>now.v+e[now.id][i].S){
mi[y]=now.v+e[now.id][i].S;
qq.push(data(mi[y],y));
}
}
}
return -1;
}
}dij;
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
class Solution {
public:
int cutOffTree(vector<vector<int>>& dd) {
int n=SZ(dd);
int m=SZ(dd[0]);
dij.init(n*m);
vector<pair<int,PII> >ppp;
ppp.PB(MP(0,MP(0,0)));
REP(i,n)REP(j,m){
if(dd[i][j]>1)ppp.PB(MP(dd[i][j],MP(i,j)));
if(dd[i][j]==0)continue;
REP(dir,4){
int nx=i+dx[dir];
int ny=j+dy[dir];
if(nx<0||ny<0||nx>=n||ny>=m)continue;
if(dd[nx][ny]==0)continue;
dij.add_edge(i*m+j,nx*m+ny,1);
}
}
sort(ALL(ppp));
int res=0;
REPP(i,1,SZ(ppp)){
LL v=dij.dis(ppp[i].S.F*m+ppp[i].S.S,ppp[i-1].S.F*m+ppp[i-1].S.S);
if(v==-1)return -1;
res+=v;
}
return res;
}
};8.36 547. Friend Circles
There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.
Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.
Example 1:
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.
Example 2:
Input:
[[1,1,0],
[1,1,1],
[0,1,1]]
Output: 1
Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends,
so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.
Note:
N is in range [1,200].
M[i][i] = 1 for all students.
If M[i][j] = 1, then M[j][i] = 1. https://leetcode.com/problems/friend-circles/
https://leetcode.com/problems/friend-circles/
class Solution {
int fbo(int i){
if(bo[i]!=i) bo[i]=fbo(bo[i]);
return bo[i];
}
void union_(int i, int j){
int b1=fbo(i), b2=fbo(j);
if(b1==b2) return;
int big=max(b1,b2), sma=min(b1,b2);
bo[sma]=big, sz[big]+=sz[sma], sz[sma]=0;
}
vector<int> bo;
vector<int> sz;
public:
int findCircleNum(vector<vector<int>>& M) {
if(M.empty() || M[0].empty()) return 0;
int R=M.size(), C=M[0].size();
bo.resize(R), sz.resize(R);
iota(bo.begin(), bo.end(), 0);
fill(sz.begin(), sz.end(), 1);
for(int i=0;i<R;++i){
for(int j=i;j<R;++j){
if(M[i][j]) union_(i,j);
}
}
return count_if(sz.begin(), sz.end(), [](int i){return i>0;});
}
};8.37 773. Sliding Puzzle
On a 2x3 board, there are 5 tiles represented by the integers 1 through 5, and an empty square represented by 0.
A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.
The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].
Given a puzzle board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.
Examples:
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]
Input: board = [[3,2,4],[1,5,0]]
Output: 14Note:
board will be a 2 x 3 array as described above.
board[i][j] will be a permutation of [0, 1, 2, 3, 4, 5].https://leetcode.com/problems/sliding-puzzle/
- BFS
class Solution {
public:
int slidingPuzzle(vector<vector<int>> &board) {
using State = vector<vector<int>>;
queue<State> q;
q.push(board);
State ending{{1, 2, 3}, {4, 5, 0}};
map<State, int> f={{board,0}}; // state to step
int dx[4] = {0, 1, 0, -1}, dy[4] = {1, 0, -1, 0};
while (!q.empty()) {
auto s = q.front(); q.pop();
if (s == ending) {
return f[s];
}
int x, y;
for (int i = 0; i < 2; ++i) {
for (int j = 0; j < 3; ++j) {
if (s[i][j] == 0) {
x = i, y = j;
}
}
}
for (int i = 0; i < 4; ++i) {
int xx = x + dx[i], yy = y + dy[i];
if (0 <= xx && xx < 2 && 0 <= yy && yy < 3) {
auto v = s;
swap(v[xx][yy], v[x][y]);
if (!f.count(v)) {
q.push(v);
f[v] = f[s] + 1;
}
}
}
}
return -1;
}
};Cannot use unordered_map here.
8.38 778. Swim in Rising Water
On an N x N grid, each square grid[i][j] represents the elevation at that point (i,j).
Now rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the total elevation of both squares is at most t. You can swim infinite distance in zero time. Of course, you must stay within the boundaries of the grid during your swim.
You start at the top left square (0, 0). What is the least time until you can reach the bottom right square (N-1, N-1)?
Example 1:
Input: [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3. When the depth of water is 3, we can swim anywhere inside the grid.
Example 2:
Input: [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation:
0 1 2 3 4
24 23 22 21 5
12 13 14 15 16
11 17 18 19 20
10 9 8 7 6The final route is marked in bold. We need to wait until time 16 so that (0, 0) and (4, 4) are connected.
Note:
2 <= N <= 50.
grid[i][j] is a permutation of [0, ..., N*N - 1].
You can't swim from (0,0) until water level is at least grid[0][0].https://leetcode.com/contest/weekly-contest-70/problems/swim-in-rising-water/
- Disjoint Set
class Solution {
public int swimInWater(int[][] a) {
int n = a.length, m = a[0].length;
DJSet ds = new DJSet(n * m);
int[] dr = { 1, 0, -1, 0 };
int[] dc = { 0, 1, 0, -1 };
for (int i = 0;; i++) { // i keeps increasing
for (int j = 0; j < n; j++) { // loop matrix
for (int k = 0; k < m; k++) {
if (a[j][k] == i) {//
for (int u = 0; u < 4; u++) {
int nj = j + dr[u], nk = k + dc[u];
if (nj >= 0 && nj < n && nk >= 0 && nk < m && a[nj][nk] <= i) {
ds.union(j * m + k, nj * m + nk);
}
}
}
}
}
if (ds.equiv(0, n * m - 1))
return i;
}
}
class DJSet { // disjoint set
public int[] upper;
public DJSet(int n) {
upper = new int[n];
Arrays.fill(upper, -1);
}
public int root(int x) {
return upper[x] < 0 ? x : (upper[x] = root(upper[x]));
}
public boolean equiv(int x, int y) {
return root(x) == root(y);
}
public void union(int x, int y) {
x = root(x);
y = root(y);
if (x != y) {
if (upper[y] < upper[x]) {
int d = x;
x = y;
y = d;
}
upper[x] = y;
}
}
}
}- BFS
const int go[4][2]={{0,-1},{0,1},{-1,0},{1,0}};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int f[55][55], N = grid.size();
queue<pair<int, int> > q;
pair<int, int> x, nx;
int u, v, uu, vv;
bool inq[55][55];
memset(inq, false, sizeof inq);
memset(f, 0x7f7f7f, sizeof f);
f[0][0] = grid[0][0];
x = make_pair(0, 0), q.push(x), inq[0][0] = true;
while (q.size())
{
x = q.front(), q.pop();
u = x.first, v = x.second;
for (int i = 0; i < 4; i++)
{
uu = u + go[i][0], vv = v + go[i][1];
if (uu >= 0 && uu < N && vv >= 0 && vv < N)
if (max(f[u][v], grid[uu][vv]) < f[uu][vv])
{
f[uu][vv] = max(f[u][v], grid[uu][vv]);
if (!inq[uu][vv])
nx = make_pair(uu, vv), q.push(nx), inq[uu][vv] = true;
}
}
inq[u][v] = false;
}
return f[N - 1][N - 1];
}
};- DFS
class Solution {
public:
int n, m;
vector<vector<int>> grid;
vector<vector<int>> vis;
void dfs(int i, int j, int v) {
if (grid[i][j] > v) return;
if (vis[i][j]) return;
vis[i][j] = true;
if (i + 1 < n) dfs(i + 1, j, v);
if (j + 1 < m) dfs(i, j + 1, v);
if (i > 0) dfs(i - 1, j, v);
if (j > 0) dfs(i, j - 1, v);
}
int swimInWater(vector<vector<int>>& grid) {
this->grid = grid;
n = grid.size();
m = grid[0].size();
for (int v = 0; v < n * m; v++) {
vis = vector<vector<int>>(n, vector<int>(m, 0));
dfs(0, 0, v);
if(vis[n - 1][m - 1]) return v;
}
return n * m;
}
};8.39 723. Candy Crush
This question is about implementing a basic elimination algorithm for Candy Crush.
Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player’s move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:
If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.You need to perform the above rules until the board becomes stable, then return the current board.
Example 1:
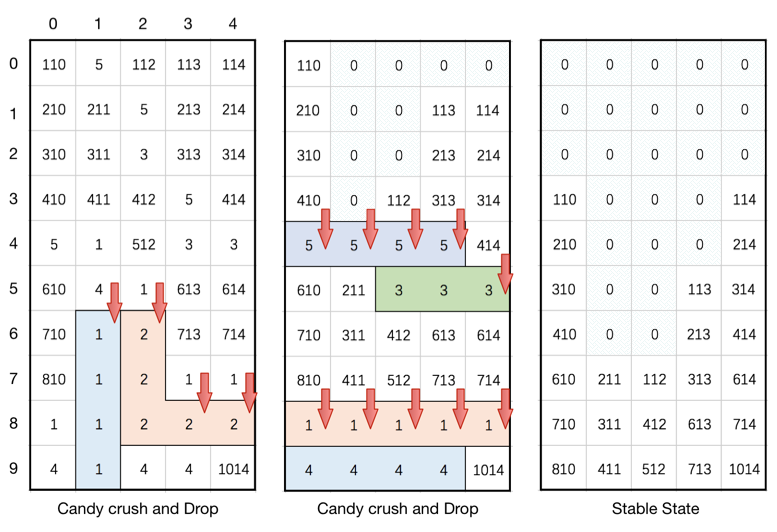
Input: board = [[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]] Output: [[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]
Explanation:
https://leetcode.com/problems/candy-crush/description/
http://www.cnblogs.com/grandyang/p/7858414.html
这道题就是糖果消消乐,博主刚开始做的时候,没有看清楚题意,以为就像游戏中的那样,每次只能点击一个地方,然后消除后糖果落下,这样会导致一个问题,就是原本其他可以消除的地方在糖果落下后可能就没有了,所以博主在想点击的顺序肯定会影响最终的stable的状态,可是题目怎么没有要求返回所剩糖果最少的状态?后来发现,其实这道题一次消除table中所有可消除的糖果,然后才下落,形成新的table,这样消除后得到的结果就是统一的了,这样也大大的降低了难度.下面就来看如何找到要消除的糖果,可能有人会想像之前的岛屿的题目一样找连通区域,可是这道题的有限制条件,只有横向或竖向相同的糖果数达到三个才能消除,并不是所有的连通区域都能消除,所以找连通区域不是一个好办法.最好的办法其实是每个糖果单独检查其是否能被消除,然后把所有能被删除的糖果都标记出来统一删除,然后在下落糖果,然后再次查找,直到无法找出能够消除的糖果时达到稳定状态.好,那么我们用一个数组来保存可以被消除的糖果的位置坐标,判断某个位置上的糖果能否被消除的方法就是检查其横向和纵向的最大相同糖果的个数,只要有一个方向达到三个了,当前糖果就可以被消除.所以我们对当前糖果的上下左右四个方向进行查看,用四个变量x0, x1, y0, y1,其中x0表示上方相同的糖果的最大位置,x1表示下方相同糖果的最大位置,y0表示左边相同糖果的最大位置,y1表示右边相同糖果的最大位置,均初始化为当前糖果的位置,然后使用while循环向每个方向遍历,注意我们并不需要遍历到头,而是只要遍历三个糖果就行了,因为一旦查到了三个相同的,就说明当前的糖果已经可以消除了,没必要再往下查了.查的过程还要注意处理越界情况,好,我们得到了上下左右的最大的位置,分别让相同方向的做差,如果水平和竖直方向任意一个大于3了,就说明可以消除,将坐标加入数组del中.注意这里一定要大于3,是因为当发现不相等退出while循环时,坐标值已经改变了,所以已经多加了或者减了一个,所以差值要大于3.遍历完成后,如果数组del为空,说明已经stable了,直接break掉,否则将要消除的糖果位置都标记为0,然后进行下落处理.下落处理实际上是把数组中的0都移动到开头,那么就从数组的末尾开始遍历,用一个变量t先指向末尾,然后然后当遇到非0的数,就将其和t位置上的数置换,然后t自减1,这样t一路减下来都是非0的数,而0都被置换到数组开头了,参见代码如下:
class Solution {
public:
vector<vector<int>> candyCrush(vector<vector<int>>& board) {
int m = board.size(), n = board[0].size();
while (true) {
vector<pair<int, int>> del;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (board[i][j] == 0) continue;
int x0 = i, x1 = i, y0 = j, y1 = j;
while (x0 >= 0 && x0 > i - 3 && board[x0][j] == board[i][j]) --x0;
while (x1 < m && x1 < i + 3 && board[x1][j] == board[i][j]) ++x1;
while (y0 >= 0 && y0 > j - 3 && board[i][y0] == board[i][j]) --y0;
while (y1 < n && y1 < j + 3 && board[i][y1] == board[i][j]) ++y1;
if (x1 - x0 > 3 || y1 - y0 > 3) del.push_back({i, j});
}
}
if (del.empty()) break;
for (auto a : del) board[a.first][a.second] = 0;
for (int j = 0; j < n; ++j) {
int t = m - 1;
for (int i = m - 1; i >= 0; --i) {
if (board[i][j]) swap(board[t--][j], board[i][j]);
}
}
}
return board;
}
};8.40 130. Surrounded Regions
Given a 2D board containing ‘X’ and ‘O’ (the letter O), capture all regions surrounded by ‘X’.
A region is captured by flipping all ’O’s into ’X’s in that surrounded region.
For example,
X X X X
X O O X
X X O X
X O X XAfter running your function, the board should be:
X X X X
X X X X
X X X X
X O X Xhttps://leetcode.com/problems/surrounded-regions/
这道题有点像围棋,将包住的O都变成X,但不同的是边缘的O不算被包围,跟之前那道Number of Islands 岛屿的数量很类似,都可以用DFS来解.刚开始我的思路是DFS遍历中间的O,如果没有到达边缘,都变成X,如果到达了边缘,将之前变成X的再变回来.但是这样做非常的不方便,在网上看到大家普遍的做法是扫面矩阵的四条边,如果有O,则用DFS遍历,将所有连着的O都变成另一个字符,比如,这样剩下的O都是被包围的,然后将这些O变成X,把变回O就行了.代码如下:
class Solution {
public:
void solve(vector<vector<char>>& board) {
if (board.empty() || board[0].empty()) return;
int m = board.size(), n = board[0].size();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
if (board[i][j] == 'O') dfs(board, i , j);
}
}
}
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (board[i][j] == 'O') board[i][j] = 'X';
if (board[i][j] == '$') board[i][j] = 'O';
}
}
}
void dfs(vector<vector<char>> &board, int x, int y) {
int m = board.size(), n = board[0].size();
vector<vector<int>> dir{{0,-1},{-1,0},{0,1},{1,0}};
board[x][y] = '$';
for (int i = 0; i < dir.size(); ++i) {
int dx = x + dir[i][0], dy = y + dir[i][1];
if (dx >= 0 && dx < m && dy > 0 && dy < n && board[dx][dy] == 'O') {
dfs(board, dx, dy);
}
}
}
};8.41 909. Snakes and Ladders
On an N x N board, the numbers from 1 to N*N are written boustrophedonically starting from the bottom left of the board, and alternating direction each row. For example, for a 6 x 6 board, the numbers are written as follows:
You start on square 1 of the board (which is always in the last row and first column). Each move, starting from square x, consists of the following:
You choose a destination square S with number x+1, x+2, x+3, x+4, x+5, or x+6, provided this number is <= N*N.
(This choice simulates the result of a standard 6-sided die roll: ie., there are always at most 6 destinations.)
If S has a snake or ladder, you move to the destination of that snake or ladder. Otherwise, you move to S.
A board square on row r and column c has a “snake or ladder” if board[r][c] != -1. The destination of that snake or ladder is board[r][c].
Note that you only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving. (For example, if the board is [[4,-1],[-1,3]], and on the first move your destination square is 2, then you finish your first move at 3, because you do not continue moving to 4.)
Return the least number of moves required to reach square N*N. If it is not possible, return -1.
Example 1:
Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]Output: 4
Explanation:
At the beginning, you start at square 1 \[at row 5, column 0\].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.
Note:
2 <= board.length = board[0].length <= 20
board[i][j] is between 1 and N*N or is equal to -1.
The board square with number 1 has no snake or ladder.
The board square with number N*N has no snake or ladder.https://leetcode.com/problems/snakes-and-ladders/description/