Chapter 5 Bit

Efficient bit manipulation is often found at the lower levels of many applications, let it be data compression, game programming, graphics manipulations, embedded control, or even efficient data representations, including databases bitmaps and indexes.

NOT: ~; Left/Right shift: <</>>; AND: &; OR: |; XOR: ^

• Set x to 0: x^=x

• Negation plus 1 is negative: ~200 + 1 = -200

• 0^x = x

• Precedence: Bitwise NOT ~ is the same as Logical NOT !.(3); << and >> Bitwise left shift and right shift. (7); 3 Bit Operators(&,^,|) have very low precedence,even lower than addition(+) and subtraction(-). (10,11,12). Refer to: http://en.cppreference.com/w/cpp/language/operator_precedence

• Bitwise NOT ~ will reverse the bit sign too. Refer to: https://stackoverflow.com/questions/7790233/how-to-clear-the-most-significant-bit

• 构造2的n次方 : \(2^n\) == 1 << n

• max uint32_t is 0xFFFFFFFF; max int32_t is 0x7FFFFFFF, min int32_t is -INT_MAX-1.

• highbit(x)

• lowbit(x) = x&-x (used by BIT. Proof of isolating the last digit is from: http://bit.ly/2xxW2og) or x&~(x-1) or x&(~x+1)

• clear_lowbit(x) = x & (x-1)

• C++ use arithmetic shift(signed shift): https://en.wikipedia.org/wiki/Arithmetic_shift .

• get_one_bit(x,i) = (x & 1<<i) >> i

• set_one_bit(x,i) = x | 1<<i

• clear_one_bit(x,i) = x & ~(1<<i). clear with a mask (like 1111110111111)

• masks: ~(1 << i),(1<<i)-1 (i 1s at least significant bits),((1<<i)-1) << (31-i)( i 1s at MSB)

• if x is \(\mathbb{Z}^+\),~x == -(x+1),so ~8 == -9

• Gray Code: n^(n>>1)

• 构造N个1: (1<<N) - 1, eg. to construct 20 1s: __builtin_popcount((1<<20)-1) == 20

• Shifting a negative signed value is undefined

• For array/string, the index starts from the left side, which is front(). But for integer, the index starts from the right side.

Bit Layout of INT_MAX, INT_MIN and -1

• ISO 9899:1999 6.5.7 Bit-wise shift operators §3

  The integer promotions are performed on each of the operands. The type of the result is that of the promoted left operand. If the value of the right operand is negative or is greater than or equal to the width of the promoted left operand, the behavior is undefined.

5.0.1 C++ Bitwise Operator

Precedence:

• Bitwise NOT ~ is the same as Logical NOT !.(3)

• << and >> Bitwise left shift and right shift. (7)

• 3 Bit Operators(&,^,|) have very low precedence,even lower than addition(+) and subtraction(-). (10,11,12)

Refer to: http://en.cppreference.com/w/cpp/language/operator_precedence

• Bitwise NOT ~ will reverse the bit sign too.

[cling]$ ~0
(int) -1

5.0.2 Fast Facts

https://stackoverflow.com/questions/7790233/how-to-clear-the-most-significant-bit

• 构造2的n次方 : \(2^n\) == 1 << (n-1)

• max uint32_t is 0xFFFFFFFF; max int32_t is 0x7FFFFFFF, min int32_t is -INT_MAX-1.

• highbit(x)

• lowbit(x) = x & -x [used by BIT]

[cling]$ int x= 0b0010101
(int) 21
[cling]$ x & -x
(int) 1
[cling]$ int y=0b01010110
(int) 86
[cling]$ y & -y
(int) 2
[cling]$ y=0b0101011000
(int) 344
[cling]$ y & -y
(int) 8

Proof of isolating the last digit is from: https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/

• clear_lowbit(x) = x & (x-1)

[cling]$ int x = 0b1001;
[cling]$ x & (x-1)
(int) 8

• C++ use arithmetic shift(signed shift): https://en.wikipedia.org/wiki/Arithmetic_shift .

• get_one_bit(x,i) = (x & 1<<i) >> i

• set_one_bit(x,i) = x | 1<<i

• clear_one_bit(x,i) = x & ~(1<<i)

clear with a mask (like 1111110111111)

[cling]$ x = 0b1001
(int) 9
[cling]$ x & ~(1 << 3)
(int) 1

• masks: ~(1 << i),(1<<i)-1 (i 1s at least significant bits),((1<<i)-1) << (31-i)( i 1s at MSB)

[cling]$ ((1<<3) -1) << (31-3)
(int) 1879048192
[cling]$ int f3(int x){int r=0;while(x && ++r) x=x&(x-1); return r;}
[cling]$ f3(1879048192)
(int) 3

• if x is \(\mathbb{Z}^+\),~x == -(x+1),so ~8 == -9

• Gray Code: n^(n>>1)

• 构造N个1: (1<<N) - 1, eg. to construct 20 1s:

[cling]$ (1<<20) - 1
(int) 1048575
[cling]$ __builtin_popcount(1048575)
(int) 20

• Shifting a negative signed value is undefined

[cling]$ -1 << 1
input_line_58:2:5: warning: shifting a negative signed value is undefined [-Wshift-negative-value]
 -1 << 1
 ~~ ^
(int) -2
[cling]$ -1 >> 1
(int) -1

5.1 Gray Code

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code,print the sequence of gray code. A gray code sequence must begin with 0.

For example,given n = 2,return [0,1,3,2]. Its gray code sequence is:

00 - 0
01 - 1
11 - 3
10 - 2

Note: For a given n,a gray code sequence is not uniquely defined.

For example,[0,2,3,1] is also a valid gray code sequence according to the above definition.

Actually there are many binary Gray code. In this question, the Gray code is called reflected binary Gray code. This code is what is usually meant in the literature by the unqualified term Gray code.

https://leetcode.com/problems/gray-code/

https://en.wikipedia.org/wiki/Gray_code

5.1.1 Algo 1: Mirror and Append

Find the pattern how the Gray code is constructed.
For 1 digit, it is [0 1].
For 2 digits, it goes like this:

[0 1]
[0 1 1 0]
[00 01 1 0]
[00 01 11 10]

So the pattern is clear:

1. current Gray code is A
2. reflect the current Gray code and get \(A\hat{A}\)
3. add 0 in the front of first A, and 1 in front of second \(\hat{A}\)

其实最后一步front变成end也行!

>>> a=[0,1]
>>> b=a[::-1]
>>> [i*2 for i in a] + [i*2+1 for i in b]
[0, 2, 3, 1]

vector<int> grayCode(int n) {
  if (n<1) return {0};
  vector<int> r = {0,1};
  for(int i=1; i<n; ++i){
    vector<int> r2 = r;
    reverse(r2.begin(), r2.end()); // reflect
    r.insert(r.end(), r2.begin(), r2.end()); // concatenate
    for_each(r.begin()+r.size()/2, r.end(), [&](int& t){t+=1<<i;}); // left append bit 1
    //copy(r.begin(), r.end(), ostream_iterator<int>(cout));cout << endl;
  }
  return r;
}

5.1.2 Algo 2: Math

Math Formular for Gray Code: \(f(n) = n \wedge (n/2)\)

Note: There are \(2^n\) gray codes for \(n\). (counting principle,subsets number of an n-element set.)

vector<int> grayCode(int n) {
  vector<int> r(1 << n,0);// preallocate 2^n space
  for (int i = 1; i<1 << n; ++i)
    r[i] = i ^ (i>>1);// Gray Code formula: n ^ (n/2)
  return r;
}

• Expand

If x is even, grayCode(x) has an even number hamming weight and if x is odd, hamming weight is odd too.

5.2 Reverse Bits

https://segmentfault.com/a/1190000003483740

http://bookshadow.com/weblog/2015/03/08/leetcode-reverse-bits/

5.2.1 Method 1

uint32_t reverseBits(uint32_t n) {
  unsigned r = 0;
  for (int i = 0; i<32; i++){
    //r = (r << 1) | (n & 1),n >>= 1;
    r <<= 1,r |= n & 1,n >>= 1;
  }
  return r;
}

5.2.2 Method 2

https://hbfs.wordpress.com/2008/08/12/bit-blenders-move-bits-around-quite-a-bit/

char tb[16] = { 0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15 };
uint32_t reverseBits(uint32_t n) {
  int curr = 0;
  uint32_t ret = 0,msk = 0xF;
  for (int i = 0; i< 8; i++) {
    ret = ret << 4;
    curr = msk&n;
    ret |= tb[curr];
    n = n >> 4;
  }
  return ret;
}

5.3 Number of 1 Bits

https://leetcode.com/problems/number-of-1-bits/

http://bookshadow.com/weblog/2015/03/10/leetcode-number-1-bits/

To use n &= (n-1) to set the right most 1 to 0, until n becomes 0.

int hammingWeight(uint32_t n) {
  int r = 0;
  while (n && ++r)
    n &= n-1;
  return r;
}

Please be noted if the function parameter is not unsigned number,we should consider the sign bit.

To use n |= n+1 to set the right most 0 to 1, until n become -1(0xffffffff).

    int hammingWeight(uint32_t n) {
        int r=0;
        int m = ~n;
        while(m!=-1 && ++r)
            m |= m+1;
        return r;
    }

Method 3 - Hacker’s Way

ppt

int hammingWeight(uint32_t x) {
  x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
  x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
  x = (x & 0x0F0F0F0F) + ((x >> 4) & 0x0F0F0F0F);
  x = (x & 0x00FF00FF) + ((x >> 8) & 0x00FF00FF);
  x = (x & 0x0000FFFF) + ((x >> 16) & 0x0000FFFF);
  return x;
}

After optimization, it becomes:

    int hammingWeight(uint32_t x) {
        x = x - ((x >> 1) & 0x55555555);
        x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
        x = (x + (x >> 4)) & 0x0F0F0F0F;
        x = x + (x >> 8);
        x = x + (x >> 16);
        return x & 0x0000003F;
    }

For even more optimization (table lookup), please read Hacker Delight chapter 5.

5.4 Counting Bits

Given a non negative integer number num. For every numbers i in the range 0 <=i <= num calculate the number of 1’s in their binary representation and return them as an array.

Example: For num = 5 you should return [0,1,1,2,1,2].

Follow up:

It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass? Space complexity should be O(n). Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.

https://leetcode.com/problems/counting-bits/

https://www.hrwhisper.me/leetcode-counting-bits/

struct Solution {
    vector<int> countBits(int num) {
        vector<int> r(num+1,0);////!!!!
        for (int i=1; i<=num; i++)
            r[i] = r[i>>1] + (i&1);
        return r;
    }
};

5.5 Repeated DNA Sequences

All DNA is composed of a series of nucleotides abbreviated as A, C, G, and T, for example: “ACGAATTCCG”. When studying DNA, it is sometimes useful to identify repeated sequences within the DNA.

Write a function to find all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule.

For example,

Given s = “AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT”,

Return: [“AAAAACCCCC”, “CCCCCAAAAA”].

https://leetcode.com/problems/repeated-dna-sequences/

这题的最优解来自类似Rabin-Karp的字符串running hash解法.

https://leetcode.com/discuss/24478/i-did-it-in-10-lines-of-c

http://oldpanda.net/2015/03/27/An-Excellent-Solution-to-Repeated-DNA-Sequences/

struct Solution {
    vector<string> findRepeatedDnaSequences(string s) {
        unordered_map<int,int> m;
        vector<string> r;
        int t = 0,i = 0,ss = s.size();
        while (i < 9)
            t = t << 3 | s[i++] & 0b111;
        while (i < ss)
            if (m[t = (t << 3) & 0x3FFFFFFF | s[i++] & 7]++==1)
                r.push_back(s.substr(i - 10,10));
        return r;
    }
};

这个构建hash值的方法太tricky,不可能在面试的时候想出来,你不可能记得所有字母的ASCII码.

关键是如何构建hash! 自己搞了一个比较笨的构造算法,用10进制. 但INT_MAX只有10位不够用,LONG_MAX有29位完全够了. 虽然笨,也beat了75%的cpp submission.

struct Solution { //122 ms
    vector<string> findRepeatedDnaSequences(string s) {
        vector<string> r;
        if(s.size()<=10) return r;
        unordered_map<long, int> counter;
        char ascii[256]={};
        ascii[(int)'A'] = 0, ascii[(int)'C'] = 1, ascii[(int)'G'] = 2, ascii[(int)'T'] = 3;
        const long BASE=1000000000; // 10 digit
        long rh=0;
        for(int i=0; i<10; ++i) rh = rh*10 + ascii[(int)s[i]]; //初始hash
        counter[rh]++;
        for(int i=1; i<s.size()-9; ++i){
            rh = rh%BASE*10 + ascii[(int)s[i+9]]; // 更新hash
            if(++counter[rh]==2) r.push_back(s.substr(i,10));;
        }
        return r;
    }
};

可不可以用其他进制比如5进制呢? 可以!

struct Solution { // 226 ms
    vector<string> findRepeatedDnaSequences(string s) {
        if(s.size()<10) return {};
        unordered_map<char,int> m{{'A',1},{'C',2},{'G',3},{'T',4}};
        map<int, int> ms;
        int h = 0;
        for(int i=0;i<10;++i)
            h = h*5 + m[s[i]];
        ms[h]++;
        // 5进制
        vector<string> r;
        int C = ((int)pow(5,10-1));
        for(int i=10;i<s.size();i++){
            h = h%C*5+m[s[i]];
            if (ms[h]++==1){
                r.push_back(s.substr(i-10+1,10));
            }
        }
        return r;
    }
};

1. 10位数,10进制下,base是10的9次方.5进制下,base是5的9次方. 注意不是10次方!!!
2. 用counter而不是set可以避免结果里面有重复字符串!

这里看到另外一种,效率会稍微好一点,因为位运算比%和*要快. 用两个比特位可以表示ACGT.10个char就是20位ACGT表示.

https://discuss.leetcode.com/topic/31640/20-ms-solution-c-with-explanation/2

struct Solution {//116 ms
    vector<string> findRepeatedDnaSequences(string s) {
        vector<string> r;
        if(s.size()<=10) return r;
        unordered_map<int, int> counter;
        char ascii[256]={};
        ascii[(int)'A'] = 0, ascii[(int)'C'] = 1, ascii[(int)'G'] = 2, ascii[(int)'T'] = 3;
        int rh=0;
        for(int i=0; i<10; ++i) rh = (rh<<2) | ascii[(int)s[i]]; //初始hash
        counter[rh]++;
        for(int i=1; i<s.size()-9; ++i){
            rh = ((rh<<2)&0b11111111111111111111) | ascii[(int)s[i+9]]; // 更新hash
            if(++counter[rh]==2) r.push_back(s.substr(i,10));;
        }
        return r;
    }
};

(rh<<2)&0b11111111111111111111的目的是把20位以上的高位消掉,因为rh<<2只会把32位之外的消掉.

二刷 4进制很顺手:

struct Solution { // 63ms, 64%
    vector<string> findRepeatedDnaSequences(string s) {
        vector<string> r;
        if(s.size()<=10) return r;
        unordered_map<char,int> m={{'A',0},{'C',1},{'G',2},{'T',3}};
        int rh=0;
        for(int i=0;i<10;++i) rh = (rh<<2) | m[s[i]];
        unordered_map<int,int> counter={{rh,1}};
        for(int i=1;i<s.size()-9;++i)
            if(++counter[rh = ((rh%(1<<18))<<2 | m[s[i+9]])]==2)
                r.push_back(s.substr(i,10));
        return r;
    }
};

Follow up:

1. 返回出现次数最多的那个序列
2. 返回所有重复过的序列in lexicographical order with O(N)

5.6 231. Power of Two

Given an integer, write a function to determine if it is a power of two.

https://leetcode.com/problems/power-of-two/

bool isPowerOfTwo(int n) {
    return n>0 && (n&(n-1))==0;
}

5.7 Single Number I

Given an array of integers, every element appears twice except for one. Find that single one.

Note: Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

https://leetcode.com/problems/single-number/

int singleNumber(vector<int>& nums) {
    int r=0;
    for_each(nums.begin(), nums.end(), [&r](int t){r^=t;});
    return r;
}

5.8 Single Number II

Given an array of integers, every element appears three times except for one. Find that single one.

Note: Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

https://leetcode.com/problems/single-number-ii/

由于x^xx = x,无法直接利用I的方法来解.但可以应用类似的思路,即利用位运算来消除重复3次的数.以一个数组[14 14 14 9]为例,将每个数字以二进制表达:

1110
1110
1110
1001
_____
4331    对每一位进行求和
1001    对每一位的和做%3运算,来消去所有重复3次的数

http://bangbingsyb.blogspot.com/2014/11/leetcode-single-number-i-ii.html

struct Solution {
    int singleNumber(vector<int>& nums, int k=3) {
        int r=0;
        for(int i=0;i<32;++i){
            int t=0;
            for(int e: nums)
                if(e & (1<<i)) ++t;
            if(t%k==1) // 1 or 0
                r |= (1<<i); // set bit
        }
        return r;
    }
};

这里是令r等于0,当那一位是1的时候set bit. 其实也可以令r全部比特位是1,r=-1,然后遇到t%k==0的时候clear bit.

struct Solution {
    int singleNumber(vector<int>& nums, int k=3) {
        int r=-1;
        for(int i=0;i<32;++i)
            if(count_if(nums.begin(), nums.end(), [](int e){return e&(1<<i);})%k==0)
                r &= ~(1<<i); // clear bit
        return r;
    }
};

当然这个题还有个hacker级别的解法: http://traceformula.blogspot.com/2015/08/single-number-ii-how-to-come-up-with.html

5.9 Single Number III

Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.

For example:

Given nums = [1, 2, 1, 3, 2, 5], return [3, 5].

Note: The order of the result is not important. So in the above example, [5, 3] is also correct. Your algorithm should run in linear runtime complexity. Could you implement it using only constant space complexity?

https://leetcode.com/problems/single-number-iii/

http://traceformula.blogspot.com/2015/09/single-number-iii-leetcode.html

struct Solution {
    vector<int> singleNumber(vector<int>& nums) {
        int t=0, r1=0, r2=0;
        for(int i: nums) t^=i;
        t&=-t;
        for(int i: nums)
            if(t&i) r1^=i; else r2^=i;
        return {r1, r2};
    }
};

5.10 Power of Four

https://leetcode.com/problems/power-of-four/

Don’t forget \(4^0==1\) and bit-wise operators has lower precedence than comparison operators \(>,<,==\).

bool isPowerOfFour(int num) {
  return (num&(num-1))==0 and (num&0x55555555)>0;
}

5.11 Subsets/PowerSet (DAG DFS)

https://en.wikipedia.org/wiki/Power_set

Subsets DFS is the most complicated DFS as the graph has every two points connecting with each other. As for the adjacency matrix, it is almost the most dense one, where all cell are 1 except diagonal cells. It is much more complicated than matrix, binary tree.

For binary tree, inside one \(dfs(\cdot)\), there are two recursive \(dfs(\cdot)\) calls because binary tree node has two children. The children number equals to the inner \(dfs(\cdot)\) calls number.

For subsets of \([a,b,c,d]\), inside one \(dfs(\cdot)\), if the current call site is at “a”, there are 3 \(dfs(\cdot)\) calls because “a” has three children; for “b”, the number becomes 2 as “b” has two children (“c” and “d”);

http://bangbingsyb.blogspot.com/2014/11/leetcode-subsets-i-ii.html

Note:

http://www.1point3acres.com/bbs/thread-117602-1-1.html

Time complexity is \(O(n*2^n)\), where n is the cardinality of the set. Space complexity is O(n).

5.11.1 DFS

C++:

struct Solution { // Runtime: 4 ms
    vector<vector<int>> subsets(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> r;
        vector<int> p;
        dfs(nums, r, p , 0);
        return r;
    }
    void dfs(vector<int>& nums, vector<vector<int>>& r, vector<int>& p, int head){
        r.push_back(p);
        for (; head<nums.size(); ++head){
            p.push_back(nums[head]);
            dfs(nums, r, p, head+1);////!!!!
            p.pop_back();
        }
    }
};

Some language specific optimization:

struct Solution {
    int L = 0, K = 0;
    vector<int> p;
    vector<vector<int>> r;
    vector<vector<int>> subsets(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        L = nums.size();
        r.resize(1<<L); // there are 2^L elements in the subsets
        dfs(nums, 0);
        return r;
    }
    void dfs(vector<int>& nums, int head){
        r[K++] = p;
        for (; head<L; ++head){
            p.push_back(nums[head]);
            dfs(nums, head+1);////!!!!
            p.pop_back();
        }
    }
};

Python:

class Solution(object):
    def subsets(self, nums):
        nums.sort()
        r, p =[], []
        self.dfs(nums, r, p, 0)
        return r
    def dfs(self, nums, r, p, head):
        r.append(list(p))####
        for i in range(head, len(nums)):
            p.append(nums[i])
            self.dfs(nums, r, p, i+1)
            p.pop()

5.11.2 Recursion

struct Solution {
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> r(1,vector<int>());
        if(nums.empty()){return r;}
        if(nums.size()==1){r.push_back(nums); return r;}
        //Elements in a subset must be in non-descending order
        sort(nums.begin(),nums.end());
        int bak = nums.back();
        nums.pop_back();
        vector<vector<int>> t = subsets(nums);// Recursion
        vector<vector<int>> t2(1, vector<int>(1, bak));
        for (int i=0;i<t.size();++i){
            if (!t[i].empty()){
                vector<int> v(t[i]);
                v.push_back(bak);
                t2.push_back(v);
            }
        }
        t.insert(t.end(),t2.begin(),t2.end());
        return t;
    }
};

Version 2:

struct Solution {
    vector<vector<int>> subsets(vector<int> &S) {
        vector<vector<int>> allSets;
        vector<int> sol;
        allSets.push_back(sol);
        sort(S.begin(), S.end());
        for(int i=0; i<S.size(); i++) {
            int n = allSets.size();
            for(int j=0; j<n; j++) {
                sol = allSets[j];
                sol.push_back(S[i]);
                allSets.push_back(sol);
            }
        }
        return allSets;
    }
};

5.11.3 Bit manipulation

struct Solution { // Runtime: 8 ms
    vector<vector<int>> subsets(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int L = nums.size(), N = 1<<L;
        vector<vector<int>> r;
        auto f=[&nums](int i){
            vector<int> r;
            for(int j=0; i!=0; i>>=1, ++j)
                if(i&1) r.push_back(nums[j]);
            return r;
        };
        for(int i=0; i<N; ++i)
            r.push_back(f(i));
        return r;
    }
};

5.12 Isolate the leftmost 1 bit

Use bit smearing, which is to say take the left most bit and make sure all the bits to its left become ones

//Explanation of bit smearing
/*1000 0000 0000 0000 0000 0000 0000 0000 (Initial)
 *1000 0000 0000 0000 1000 0000 0000 0000 (x |= x >> 16)
 *1000 0000 1000 0000 1000 0000 1000 0000 (x |= x >> 8)
 *1000 1000 1000 1000 1000 1000 1000 1000 (x |= x >> 4)
 *1010 1010 1010 1010 1010 1010 1010 1010 (x |= x >> 2)
 *1111 1111 1111 1111 1111 1111 1111 1111 (x |= x >> 1)*/
x |= x >> 16;
x |= x >> 8;
x |= x >> 4;
x |= x >> 2;
x |= x >> 1;
//Now get only the original leftmost
x ^= x >> 1;

5.13 405. Convert a Number to Hexadecimal

Given an integer, write an algorithm to convert it to hexadecimal. For negative integer, two’s complement method is used.

Note:
All letters in hexadecimal (a-f) must be in lowercase.
The hexadecimal string must not contain extra leading 0s. If the number is zero, it is represented by a single zero character ‘0’; otherwise, the first character in the hexadecimal string will not be the zero character.
The given number is guaranteed to fit within the range of a 32-bit signed integer.
You must not use any method provided by the library which converts/formats the number to hex directly.

Example 1:
Input: 26; Output: “1a”

Example 2:
Input: -1; Output: “ffffffff”

https://leetcode.com/problems/convert-a-number-to-hexadecimal/

http://www.cnblogs.com/grandyang/p/5926674.html

string toHex(int num) {
    string r, s="0123456789abcdef";
    int i = 8;
    while (num && i--)
        r = s[(num & 0xf)] + r, num >>= 4;
    return r.empty() ? "0" : r;
}

由于整形提升,'0'+t的结果变成了integer,所以必须加char转换回来.

http://simpleyyt.github.io/2016/11/13/cpp-type-conversion

Typecasting in C and C++

There is a similar problem related to number system conversion math-probability.

5.14 Floating Point Number

Real numbers(\(\mathbb{R}\)) have a totally different format,and they need an altogether different processor architecture to perform arithmetic operations with them.

5.15 Floating Point Number

内存表示:

Mantissa也叫significand.

Bias equals to 127 for single precision, 1024 for double precision. This yields exponent ranges from −126 to +127 for single precision and −1022 to +1023 for double precision.

\[N = (-1)^s \cdot Mantissa \cdot 2^{E-bias}\]

All fractional numbers, which can be exactly represented in binary system, can be written as \(M * 2^N\) where M and N are both integers. 就是说所有二进制系统能精确表示的小数,都是2的N次方的整数倍.比如0.5, 0.25, 0.125.

In C++, to be able to compare to floating point number, you must be able to exactly represent it in binary format first! - Fuheng

比如在程序中比较一个浮点数是否等于0.125,可以直接用等于号.

[cling]$ double d=0.125;
[cling]$ bool b=d==0.125;
[cling]$ b
(bool) true
[cling]$ double d2=0.124;
[cling]$ b=d==0.124;
[cling]$ b
(bool) false

Pure Storage OA面经: http://www.1point3acres.com/bbs/thread-118986-1-1.html

3,判断下列哪些小数有确定有限的(exact)二进制表示: A 0.1, B 0.2, C 0.3, D 0.4, E 0.5

浮点数分三类:

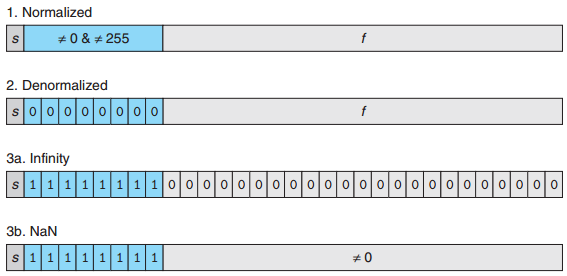
注意NAN可以有多种内存表示.

Computer Systems: A Programmer’s Perspective, P102.

• Why does IEEE 754 reserve so many NaN values?

The IEEE-754 standard defines a NaN as a number with all ones in the exponent, and a non-zero significand. The highest-order bit in the significand specifies whether the NaN is a signaling NAN or quiet NAN. The remaining bits of the significand form what is referred to as the payload of the NaN.

Whenever one of the operands of an operation is a NaN, the result is a NaN, and the payload of the result equals the payload of one of the NaN operands. Payload preservation is important for efficiency in scientific computing, and at least one company has proposed using NaN payloads for proprietary uses.

In more basic terms, a NaN doesn’t carry any useful numerical information, and the entire 32 bits must be reserved anyway, so the unused bits in the significand would be otherwise wasted if there were not a payload defined in the standard.

From: https://goo.gl/aT4GDi

• What is the purpose of NaN boxing?

See: https://goo.gl/K9pOA7

FLT_MAX: 3.40282e+38
DBL_MAX: 1.79769e+308

在C99里面可以直接用.

2017(7-9月) 码农类 硕士 全职 Google - Other - Onsite |Other在职跳槽 新鲜出炉的狗家面经 5道算法, 1道system design. 3道leetcode 原题. 289 game of life, 380/381 getRandom, 302 smallest rectangle.. 1道LRU 变种、1道我没有想出来的float list 优于nlogn time 的 sort 算法. 系统设计 google ads. 高QPS. 虽没有出结果, 目测已跪在那倒sort list 的题目上. 发帖祝福大家都拿到心仪offer. (p.s. 公司最近lay off 我们整组人, 待业青年,有哪位好心人路过,求内推).

http://www.1point3acres.com/bbs/thread-289095-1-1.html
http://www.boost.org/doc/libs/1_66_0/libs/sort/doc/html/index.html
https://en.wikipedia.org/wiki/American_flag_sort

How to count set bits in a floating point number in C?

https://www.geeksforgeeks.org/count-set-bits-floating-point-number/

http://graphics.stanford.edu/~seander/bithacks.html

5.16 BIT(Binary Index Tree)

• Count of Smaller Numbers After Self

https://leetcode.com/problems/count-of-smaller-numbers-after-self/

• The Skyline Problem

https://leetcode.com/problems/the-skyline-problem/

5.17 Bitmap/Bitarray

Bitmap is good for problem of pick-or-not. I can remember questions like powerset, N-queens off the top of my head.

5.18 N-Queens

https://leetcode.com/problems/n-queens/

复杂度: https://en.wikipedia.org/wiki/Eight_queens_puzzle#Counting_solutions

Method 1:

N皇后问题是非常经典的问题了,记得当时搞竞赛第一道递归的题目就是N皇后.因为这个问题是典型的NP问题,所以在时间复杂度上就不用纠结了,肯定是指数量级的.下面我们来介绍这个题的基本思路. 主要思想就是一句话:用一个循环递归处理子问题.这个问题中,在每一层递归函数中,我们用一个循环把一个皇后填入对应行的某一列中,如果当前棋盘合法,我们就递归处理先一行,找到正确的棋盘我们就存储到结果集里面. 这种题目都是使用这个套路,就是用一个循环去枚举当前所有情况,然后把元素加入,递归,再把元素移除,这道题目中不用移除的原因是我们用一个一维数组去存皇后在对应行的哪一列,因为一行只能有一个皇后,如果二维数组,那么就需要把那一行那一列在递归结束后设回没有皇后,所以道理是一样的.

这道题最后一个细节就是怎么实现检查当前棋盘合法性的问题,因为除了刚加进来的那个皇后,前面都是合法的,我们只需要检查当前行和前面行是否冲突即可.检查是否同列很简单,检查对角线就是行的差和列的差的绝对值不要相等就可以.

这道题实现的方法是一个非常典型的套路,有许多题都会用到,基本上大部分NP问题的求解都是用这个方式,比如Sudoku Solver,Combination Sum,Combinations,Permutations,Word Break II,Palindrome Partitioning等,所以大家只要把这个套路掌握熟练,那些题就都不在话下哈.

http://blog.csdn.net/linhuanmars/article/details/20667175

https://segmentfault.com/a/1190000003762668

Method 2:

Refer to matrix too.

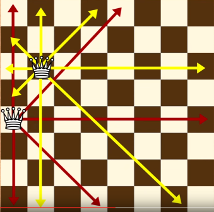
http://jsomers.com/nqueen_demo/nqueens.html

https://www.youtube.com/watch?v=jPcBU0Z2Hj8

https://discuss.leetcode.com/topic/13617/accepted-4ms-c-solution-use-backtracking-and-bitmask-easy-understand?show=108056

We can use three arrays to indicate if the column or the diagonals had a queen before. If not, we can put a queen in this position and continue.

using VS = vector<string>;
using VVS = vector<VS>;
struct Solution {//Your runtime beats 78.57% of cpp submissions.
  VVS solveNQueens(int n) {
    VS p(n, string(n, '.')); VVS r;
    dfs(p, 0, n, 0LL, 0LL, 0LL, r);
    return r;
  }
  void dfs(VS &p,int row,int n,long long cb,long long m1,long long m2,VVS &r){
    if(n==row){ r.push_back(p); return; }
    for(int i=0;i<n;++i){// i is col here
      if( (cb&(1LL<<i)) || (m1&(1LL<<(i+row))) || (m2&(1LL<<(n-1+i-row))))
        continue;// get bit
      p[row][i]='Q';
      dfs(p,row+1,n,cb|(1LL<<i),m1|(1LL<<(i+row)),m2|(1LL<<(n+i-1-row)),r);// set bit
      p[row][i]='.';
    }
  }
};

Extension:

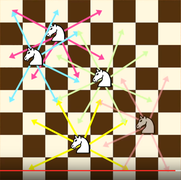
Knight’s Tour Problem: bloomberg-2017.html#knights-tour

https://github.com/xiw/splay/blob/master/test/nqueens.c

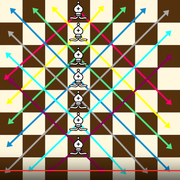
5.19 N-Queens II

https://leetcode.com/problems/n-queens-ii/

using VS = vector<string>;
using VVS = vector<VS>;
struct Solution {
  int totalNQueens(int n) {
    int r=0;
    dfs(0, n, 0LL, 0LL, 0LL, r);
    return r;
  }
  void dfs(int row,int n,long long cb,long long m1,long long m2,int& r){
    if(n==row){ r++; return; }
    for(int i=0;i<n;++i){// i is col here
      if( (cb&(1LL<<i)) || (m1&(1LL<<(i+row))) || (m2&(1LL<<(n-1+i-row))))
        continue;// get bit
      dfs(row+1,n,cb|(1LL<<i),m1|(1LL<<(i+row)),m2|(1LL<<(n+i-1-row)),r);// set bit
    }
  }
};

另一种方法:

struct Solution {
  int totalNQueens(int n) { return dfs(0, n, 0LL, 0LL, 0LL); }
  int dfs(int row,int n,long long cb,long long m1,long long m2){
    if(n==row){ return 1; } // leaf node of the tree
    int r=0;
    for(int i=0;i<n;++i){// i is col here
      if( (cb&(1LL<<i)) || (m1&(1LL<<(i+row))) || (m2&(1LL<<(n-1+i-row))))
        continue;// get bit
      r += dfs(row+1,n,cb|(1LL<<i),m1|(1LL<<(i+row)),m2|(1LL<<(n+i-1-row)));// set bit
    }
    return r;
  }
};

5.20 Bloomfilter

Bloom filter is a probabilistic data structure: it tells us that the element either definitely is not in the set or may be in the set.

5.21 Binary Trie

Refer array for other trie details.

5.22 Maximum XOR of Two Numbers in an Array

https://leetcode.com/problems/maximum-xor-of-two-numbers-in-an-array/

Given a non-empty array of numbers, \(a_0, a_1, a_2, ..., a_{n-1}\), where \(0 \le a_i &lt; 2^{31}\).

Find the maximum result of ai XOR aj, where \(0 \le i, j &lt; n\).

Could you do this in \(O(n)\) runtime?

Example:

Input: [3, 10, 5, 25, 2, 8]

Output: 28

Explanation: The maximum result is \(5 \wedge 25 = 28\).

Method 1: Divide and Conquer

http://bookshadow.com/weblog/2016/10/15/leetcode-maximum-xor-of-two-numbers-in-an-array/

// Your runtime beats 83.68% of cpp submissions.
struct Solution {
  int findMaximumXOR(vector<int>& nums) {
    if (nums.size()<2) return 0;
    return f(nums, 1 << 30); // all ints are positive
  }
  int f(const vector<int>& v, int mask) {
    vector<int> v0, v1;
    for (int i : v) if (i&mask) v1.push_back(i); else v0.push_back(i);
    if (v0.empty())
      return f(v1, mask >> 1);
    else if (v1.empty())
      return f(v0, mask >> 1);
    else
      return mask + f2(v0, v1, mask >> 1);
  }
  int f2(const vector<int>& v0, const vector<int>& v1, int mask) {
    if (mask == 0) return 0;
    vector<int> v00, v01, v10, v11;
    for (int i : v0) if (i&mask) v01.push_back(i); else v00.push_back(i);
    for (int i : v1) if (i&mask) v11.push_back(i); else v10.push_back(i);

    int r = 0, r0 = 0, r1 = 0;
    if (!v00.empty() && !v11.empty()) r0 = mask + f2(v00, v11, mask >> 1);
    if (!v01.empty() && !v10.empty()) r1 = mask + f2(v01, v10, mask >> 1);
    r = max(r0, r1);
    if (r == 0) // for this bit, you cannot find any XOR result == 1
      r = f2(v0, v1, mask >> 1);
    return r;
  }
};

Method 2: Bit Trie

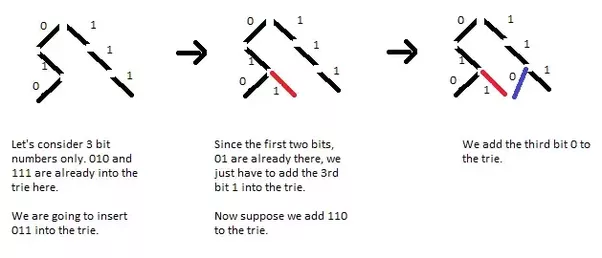
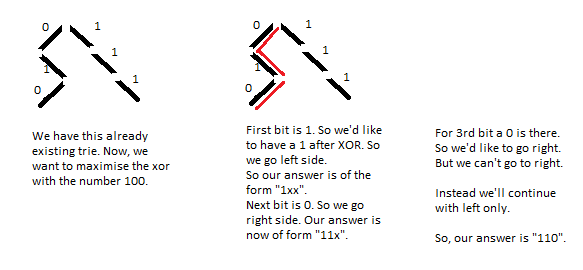
https://threads-iiith.quora.com/Tutorial-on-Trie-and-example-problems

Note:

[cling]$ 1<<31
(int) -2147483648
[cling]$ 1L<<31
(long) 2147483648
[cling]$ -(1L<<31) == (1<<31)
(bool) true

// 69 ms. Your runtime beats 95.82% of cpp submissions.
struct trie_node { trie_node* next[2] = {}; };
trie_node* create_btrie() { return new trie_node(); }
void add(trie_node* cur, int i, long long mask) { // O(K)
  while (mask) {
    int idx = (i&mask) ? 1 : 0;
    if (!cur->next[idx])
      cur->next[idx] = new trie_node();
    cur = cur->next[idx];
    mask >>= 1;
  }
}
int query_maxxor(trie_node* cur, int i, long long mask) {
  long long r = 0;
  while (mask) { // O(K)
    int idx0 = (i&mask) ? 0 : 1;
    if (cur->next[idx0]) {
      r += mask;
      cur = cur->next[idx0];
    } else
        cur = cur->next[(i&mask) ? 1 : 0];
    mask >>= 1;
  }
  return r;
}
struct Solution {//O(NK) K=Log(mx)
  int findMaximumXOR(vector<int>& nums) {
    if (nums.size()<2) return 0;
    int mx = *max_element(nums.begin(), nums.end());//O(N)
    long long int mask = 1;
    while (mx) { mx >>= 1, mask<<=1; } //O(K)
    mask>>=1;
    trie_node* root = create_btrie();
    for (int i : nums) // O(N)
      add(root, i, mask);
    int r = 0;
    for (int i : nums) // O(N)
      r = max(r, query_maxxor(root, i, mask));
    return r;
  }
};

This is the simplest trie, no data stored in the tree node.

5.23 Integer Compression

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=206769

第四轮(国人小哥):一个int,比如2,转换为bit,前面都是0,只有后面最后两位有个1和0(0000…….00010)表示是2,所以前面那些0占的空间就很浪费.小哥要设计一个protocol(写两个function,一个serialize,一个deserialize),给一个int,然后把这个int转换成另外一种形式,这种形式是一个List,Byte总共8位,第一位是0/1,用作flag表示后面还有没有后续的Byte,剩余7位是这个数字de值.比如输入是2,输出就是一个list,里面只包含1个Byte,这个Byte从头到尾是0|0000010.如果输入是个很大的数(比如他转换为32位是0000..000001000001000000000),那输出就是list,里面包含多个Byte,头几个Byte可能是1|0000000, 1|0000100,最后一个是0|0000010. 好心的面试官给了不少关于位运算的提示,要不就做不完了.

vector<char> _serialize(int i){
  int k=4;
  while(k){
    if((i >> k*7)!=0) break;
    k--;
  }
  if(k==0) return {0};
  vector<char> r(k+1, 1<<7);
  r[0] = 0;
  for(int j=0;j<=k;++j)
    r[j] |= ((i & (127<<j*7)) >> j*7);
  reverse(r.begin(), r.end());
  return r;
}
vector<char> serialize(vector<int> is){
  vector<char> r;
  for(int i: is){
    vector<char> t=_serialize(i);
    r.insert(r.end(), t.begin(), t.end());
  }
  return r;
}
vector<int> deserialize(vector<char> v){
  vector<int> r;
  int i=0;
  for(char c: v){
    i <<= 7, i |= (c & 127);
    if(!(c & 128)){
      r.push_back(i), i=0;
    }
  }
  return r;
}

5.24 Next or Previous Power of 2

http://www.geeksforgeeks.org/next-power-of-2/

unsigned int nextPowerOf2(unsigned int n){
    if (n && !(n & (n - 1))) return n;
    unsigned int p = 1;
    while (p < n) p <<= 1;
    return p;
}

用类似bit smearing的方法:

unsigned int nextPowerOf2(unsigned int n){
  n--;
  int m=1;
  while(m != (1<<4)) n|=n>>m, m<<=1;
  return n+1;
}

其实用这个方法最简单:bit.html#isolate-the-leftmost-1-bit

其实就是把最高位再向左移动一位即可!!!

这个帖子写的方法都菜http://www.geeksforgeeks.org/highest-power-2-less-equal-given-number/.最有效的方法是这个:

uint_32t highestPowerof2(uint32_t x) {
    if (x && !(x & (x - 1))) return x;
    x |= x >> 16;
    x |= x >> 8;
    x |= x >> 4;
    x |= x >> 2;
    x |= x >> 1;
    x ^= x >> 1;
    return x;
}

• n|1 next odd number: 10 -> 11
  
• n>>1<<1 previous even number: 11 -> 10

5.25 461. Hamming Distance

The Hamming distance between two integers is the number of positions at which the corresponding bits are different.

Given two integers x and y, calculate the Hamming distance.

Note:
0 <= x, y < \(2^31\).

Example:

Input: x = 1, y = 4

Output: 2

Explanation:

1   (0 0 0 1)
4   (0 1 0 0)
       ?   ?

The above arrows point to positions where the corresponding bits are different.

https://leetcode.com/problems/hamming-distance

int hammingDistance(int x, int y) {
    return __builtin_popcount(x^y);
}

5.26 477. Total Hamming Distance

The Hamming distance between two integers is the number of positions at which the corresponding bits are different.

Now your job is to find the total Hamming distance between all pairs of the given numbers.

Example:

Input: 4, 14, 2

Output: 6

Explanation: In binary representation, the 4 is 0100, 14 is 1110, and 2 is 0010 (just showing the four bits relevant in this case). So the answer will be: HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.

Note:

Elements of the given array are in the range of 0 to 10^9
Length of the array will not exceed 10^4.

这里如果使用双重循环一个个比较两个数字的差异,可以算出来,但是在时间上会有用例超时.
T: \(O(N^2)\) S: \(O(1)\)

int totalHammingDistance(vector<int>& nums) {
    int r=0;
    for(int i=0;i<nums.size();++i)
        for(int j=i+1;j<nums.size();++j)
            r+=__builtin_popcount(nums[i] ^ nums[j]);
    return r;
}

这里换一种思路,我们看每个数都有32位,对每一位,我们统计数组中的数再这一位上为1的有几个数,那么在这一位上,所有两对数不同的情况是为1的数量乘以为0的数量,是个排列组合的问题.对每一位我们都这样操作,就可以很快得出结果了.
T: \(O(32*N)\) S: \(O(1)\)

int totalHammingDistance(vector<int>& nums) {
    int r=0, L=nums.size();
    for(int i=0;i<sizeof(int)*8;++i){
        int j=0;
        for(int e: nums) j+=(e&(1<<i))>>i;
        r+=j*(L-j);
    }
    return r;
}

5.27 318. Maximum Product of Word Lengths

Given a string array words, find the maximum value of length(word[i]) * length(word[j]) where the two words do not share common letters. You may assume that each word will contain only lower case letters. If no such two words exist, return 0.

Example 1:

Given [“abcw”, “baz”, “foo”, “bar”, “xtfn”, “abcdef”]
Return 16
The two words can be “abcw”, “xtfn”.

Example 2:

Given [“a”, “ab”, “abc”, “d”, “cd”, “bcd”, “abcd”]
Return 4
The two words can be “ab”, “cd”.

Example 3:

Given [“a”, “aa”, “aaa”, “aaaa”]
Return 0
No such pair of words.

https://leetcode.com/problems/maximum-product-of-word-lengths

这道题给我们了一个单词数组,让我们求两个没有相同字母的单词的长度之积的最大值.我开始想的方法是每两个单词先比较,如果没有相同字母,则计算其长度之积,然后每次更新结果就能找到最大值.但是我开始想的两个单词比较的方法是利用哈希表先将一个单词的所有出现的字母存入哈希表,然后检查另一个单词的各个字母是否在哈希表出现过,若都没出现过,则说明两个单词没有相同字母,则计算两个单词长度之积并更新结果.但是这种判断方法无法通过OJ的大数据集,上网搜大神们的解法,都是用了mask,因为题目中说都是小写字母,那么只有26位,一个整型数int有32位,我们可以用后26位来对应26个字母,若为1,说明该对应位置的字母出现过,那么每个单词的都可由一个int数字表示,两个单词没有共同字母的条件是这两个int数想与为0,用这个判断方法可以通过OJ,参见代码如下:

T: \(O(M*N^2)\) S: \(O(1)\) where M is average size of string, N is size of vector.

int maxProduct(vector<string>& words) {
    vector<int> v;
    int r=0;
    for(string& s: words){
        int i=0;
        for_each(s.begin(), s.end(), [&i](char c){i|=(1<<(c-'a'));});
        for(int j=0;j<v.size();++j)
            if((i&v[j]) == 0)
                r=max(r, int(words[j].size() * s.size()));
        v.push_back(i);
    }
    return r;
}

利用int做bucket,做一个特殊的hash.

5.28 201. Bitwise AND of Numbers Range

Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive.

For example, given the range [5, 7], you should return 4.

https://leetcode.com/problems/bitwise-and-of-numbers-range/ 先从题目中给的例子来分析,[5, 7]里共有三个数字,分别写出它们的二进制为:

101　　110　　111

相与后的结果为100,仔细观察我们可以得出,最后的数是该数字范围内所有的数的左边共同的部分,如果上面那个例子不太明显,我们再来看一个范围[26, 30],它们的二进制如下:

11010　　11011　　11100　　11101　　11110

发现了规律后,我们只要写代码找到左边公共的部分即可

http://www.cnblogs.com/grandyang/p/4431646.html

int rangeBitwiseAnd(int m, int n) {
    int i=0;
    while(m!=n) m>>=1, n>>=1, i++;
    return m<<i;
}

5.29 389. Find the Difference

Given two strings s and t which consist of only lowercase letters.

String t is generated by random shuffling string s and then add one more letter at a random position.

Find the letter that was added in t.

Example:

Input:
s = "abcd"
t = "abcde"

Output:
e

Explanation:
'e' is the letter that was added.

char findTheDifference(string s, string t) {
    char r=0;
    for_each(s.begin(), s.end(), [&r](char c){r^=c;});
    for_each(t.begin(), t.end(), [&r](char c){r^=c;});
    return r;
}

5.30 401. Binary Watch

A binary watch has 4 LEDs on the top which represent the hours (0-11), and the 6 LEDs on the bottom represent the minutes (0-59).

Each LED represents a zero or one, with the least significant bit on the right.

For example, the above binary watch reads “3:25”.

Given a non-negative integer n which represents the number of LEDs that are currently on, return all possible times the watch could represent.

Example:

Input: n = 1 Return: [“1:00”, “2:00”, “4:00”, “8:00”, “0:01”, “0:02”, “0:04”, “0:08”, “0:16”, “0:32”]

Note: The order of output does not matter. The hour must not contain a leading zero, for example “01:00” is not valid, it should be “1:00”. The minute must be consist of two digits and may contain a leading zero, for example “10:2” is not valid, it should be “10:02”.

https://leetcode.com/problems/binary-watch/

vector<string> readBinaryWatch(int num) {
    vector<string> r;
    for(int i=0;i<1024;++i)
        if(__builtin_popcount(i)==num) {
            int h=(i&0x3C0) >> 6, m=i&0x3F;
            if(h>=12 || m>=60) continue;
            r.push_back(to_string(h) + ":" + (m>9?to_string(m):("0"+to_string(m))));
        }
    return r;
}

5.31 476. Number Complement

Given a positive integer, output its complement number. The complement strategy is to flip the bits of its binary representation.

Note:
The given integer is guaranteed to fit within the range of a 32-bit signed integer. You could assume no leading zero bit in the integer’s binary representation.

Example 1:

Input: 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.

Example 2:

Input: 1
Output: 0
Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.

https://leetcode.com/problems/number-complement/

struct Solution {
    int findComplement(int num) {
        int t=num, r=1;
        while(t) t>>=1, r<<=1;
        return (r-1)^num;
    }
};

5.32 320. Generalized Abbreviation

Write a function to generate the generalized abbreviations of a word.

Example:
Given word = “word”,return the following list (order does not matter):

[“word”,“1ord”,“w1rd”,“wo1d”,“wor1”,“2rd”,“w2d”,“wo2”,“1o1d”,“1or1”,“w1r1”,“1o2”,“2r1”,“3d”,“w3”,“4”]

https://leetcode.com/problems/generalized-abbreviation/

http://smartyi8979.com/2016/03/22/Generalized-Abbreviation/

http://blog.csdn.net/hjf0416/article/details/50461816

This is an extension of power set problem.

5.32.1 Algo 1: Bit Manipulation

// Runtime: 180 ms. Your runtime beats 11.52% of cppsubmissions.
vector<string> generateAbbreviations(string word) {
  int L = word.size();
  auto getstr = [&word,&L](int n) {
    string s(L,'1'), r; // '1' is just a special character
    for (int i = 0; i<L; ++i) if (n&(1<<i)) s[i] = word[i];
    int c = 0;
    for (char ch : s)
      if (ch == '1') c++;
      else if (c>0) r += to_string(c) + ch,c = 0;
      else r += ch;
    if (c) r += to_string(c);
    return r;
  };
  vector<string> r(1<<L);
  for (int i = 0; i<(1<<L); ++i)
    r[i] = getstr(i);
  return r;
}

Also I can use inplace conversion,the speed is as twice as the previous one,but code is more complex.

// Runtime: 64 ms. Your runtime beats 98.03% of cppsubmissions.
vector<string> generateAbbreviations(string word) {
  int L = word.size();
  auto getstr = [&word,&L](int n) {
    string r(L,'1');
    for (int i = 0; i<L; ++i)
      if (n&(1 << i)) r[i] = word[i];
    string t;
    int i = 0,j = 0,c = 0; // Two pointers: inplace conversion 11d11 -> 2d2
    for (; j<L; ++j) // 111111111111 -> 12
      if (r[j] == '1')
        c++;
      else
        if (c == 0)
          r[i++] = r[j];
        else if (c>0 && c<10)
          r[i++] = '0' + c,r[i++] = r[j],c = 0;
        else if (c >= 10) {
          t = to_string(c);
          for (char ch : t) r[i++] = ch;
          r[i++] = r[j],c = 0;
        }
        if (c>0 && c<10)
          r[i++] = '0' + c;
        else if (c >= 10) {
          t = to_string(c);
          for (char ch : t) r[i++] = ch;
        }
        r.resize(i);
        return r;
  };
  int k = pow(2,L);
  vector<string> r(k,"");
  r[0]=to_string(L),r[k-1] = word;// 4ms optimization
  for (int i=1; i<k-1; ++i)
    r[i] = getstr(i);
  return r;
}

5.32.2 DFS

struct Solution { // Runtime: 56 ms. Your runtime beats 99.72% of cppsubmissions.
  int L = 0;
  int k = 0;
  string tmp;
  string lstr;

  vector<string> generateAbbreviations(string word) {
    L = word.size();
    vector<string> r(1 << L,"");
    r[k++] = word;
    dfs(r,word,L,0);
    return r;
  }
private:
  void dfs(vector<string>& r,string cur,int num,int idx) {
    int csz = cur.size();
    for (int i = idx; i < L; ++i) {
      for (int len = 1; len <= num && i + len - 1 < csz; ++len) {
        tmp = cur,lstr = to_string(len);
        tmp.replace(i,len,lstr);
        r[k++] = tmp;
        dfs(r,tmp,num,lstr.size() - ~i);
      }
    }
  }
};

5.33 411. Minimum Unique Word Abbreviation

A string such as “word” contains the following abbreviations:

[“word”, “1ord”, “w1rd”, “wo1d”, “wor1”, “2rd”, “w2d”, “wo2”, “1o1d”, “1or1”, “w1r1”, “1o2”, “2r1”, “3d”, “w3”, “4”]

Given a target string and a set of strings in a dictionary, find an abbreviation of this target string with the smallest possible length such that it does not conflict with abbreviations of the strings in the dictionary. Each number or letter in the abbreviation is considered length = 1. For example, the abbreviation “a32bc” has length = 4.

Note:
- In the case of multiple answers as shown in the second example below, you may return any one of them.
- Assume length of target string = m, and dictionary size = n. You may assume that m <= 21, n <= 1000, and log2(n) + m <= 20.

Examples:
“apple”, [“blade”] -> “a4” (because “5” or “4e” conflicts with “blade”)
“apple”, [“plain”, “amber”, “blade”] -> “1p3” (other valid answers include “ap3”, “a3e”, “2p2”, “3le”, “3l1”)

https://leetcode.com/problems/minimum-unique-word-abbreviation

可以用0,1来表示取舍. 难点是对长度的定义发生了变化,所以要自己写个求长度的函数:

class Solution {
    string get_abbrev(string& s, int i){ // i is meta data
        string t=s, r;
        for(int k=0;k<s.size();++k)
            if(i&(1<<k)) t[k]='-';
        int k=0;
        for(char c: t)
            if(c=='-') k++; else if(k==0) r+=c; else r+=to_string(k)+c,k=0;
        if(k) r+=to_string(k);
        return r;
    }
    int getsize(string& s){
        int l=0, b=0;
        for(char c: s)
            if(!isdigit(c)) ++l, b=0; else if(!b) l++, b=1;
        return l;
    }
public:
    string minAbbreviation(string target, vector<string>& dictionary) {
        if(dictionary.empty()) return to_string(target.size());
        int L=target.size(), l=INT_MAX;
        string r;
        for(int i=0; i<(1<<L); ++i){
            string t=get_abbrev(target, i);
            bool found_conflict=false;
            for(string& s: dictionary)
                if(t==get_abbrev(s, i)){ found_conflict=true; break; }
            int k;
            if(!found_conflict && (k=getsize(t))<l) r=t, l=k;
        }
        return r;
    }
};

这个代码逻辑正确但是会TLE.必须要优化.如果已经知道当前最小长度为l,如果在构建字典里面的值的abbrev的时候算到长度已经等于这个值了,继续算下去只会越来越多,这时候就可以提前返回了.需要修改的代码如下:

string get_abbrev(string& s, int i, int m=INT_MAX){ // i is meta data
    string t(s.size(),'-'), r;
    int sz=0;
    for(int k=0;k<s.size();++k)
        if(i&(1<<k)){ t[k]=s[k]; sz++; if(sz>=m) return "";}
    int k=0;
    for(char c: t)
        if(c=='-') k++; else if(k==0) r+=c; else r+=to_string(k)+c,k=0;
    if(k) r+=to_string(k);
    return r;
}
string minAbbreviation(string target, vector<string>& dictionary) {
    if(dictionary.empty()) return to_string(target.size());
    int L=target.size(), l=INT_MAX;
    string r, t;
    for(int i=0; i<(1<<L); ++i){
        if((t=get_abbrev(target, i, l)).empty()) continue;
        bool found_conflict=false;
        for(string& s: dictionary){
            string b=get_abbrev(s, i, l);
            if(!b.empty() && t==b){ found_conflict=true; break; }
        }
        int k;
        if(!found_conflict && (k=getsize(t))<l) r=t, l=k;
    }
    return r;
}

这样可以提交通过了.其实还有很多可以优化的地方,这里暂时略过.

5.34 779. K-th Symbol in Grammar

On the first row, we write a 0. Now in every subsequent row, we look at the previous row and replace each occurrence of 0 with 01, and each occurrence of 1 with 10.

Given row N and index K, return the K-th indexed symbol in row N. (The values of K are 1-indexed.) (1 indexed).

Examples:
Input: N = 1, K = 1
Output: 0

Input: N = 2, K = 1
Output: 0

Input: N = 2, K = 2
Output: 1

Input: N = 4, K = 5
Output: 1

Explanation:
row 1: 0
row 2: 01
row 3: 0110
row 4: 01101001

Note:

N will be an integer in the range [1, 30].
K will be an integer in the range [1, 2^(N-1)].

https://leetcode.com/problems/k-th-symbol-in-grammar/description/

class Solution {
public:
    int kthGrammar(int N, int K) {
        return bitset<32>(K - 1).count() & 1;
    }
};

class Solution {
  public int kthGrammar(int N, int K) {
      return Integer.bitCount(K-1)%2;
  }
}

5.35 Morse Code

https://www.codechef.com/problems/CIT04

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=3554

5.36 Bit Manipulation Practice

https://leetcode.com/tag/bit-manipulation/