Chapter 30 Combinatorics

DFS + DP

Combinatorics的题两种. 一是让你数数,一般动态规划DP求解; 一是让你返回所有可行解,必须DFS.

https://discuss.leetcode.com/topic/52542/c-template-for-all-combination-problem-set

• Counting Principle

Probability Theory里面的counting principle仅仅适用于比较规则的情况(counting principle要求每一个可能的结果的下一步的可能结果数目也相同),当然做起来非常快.比如洗下面的情况,1,2,3之后都有2种可能,所以可以用乘法2x3=6得到结果.

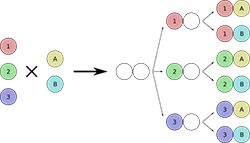
计算机用来做这个事情有它的长处,就是更加的generic,可以处理很多复杂的情况.用树来表示,子节点数就是下一步的可能选择的数目.We can use DFS to traverse the tree until we reach leaf nodes. When we reach leaf node, we do cherry pick by increasing counter by 1. We can do pruning when traversing in order to speed up the process.

The number of valid leaf nodes is the result of our counting. DFS比较heavy的原因是它会找到每条path,有时候题目并不需要这个path的信息.

• Duplicates Removing

set去重太heavy,最好的办法是sort之后用大小关系剪枝(Pruning)去重.

30.1 447. Number of Boomerangs

Given n points in the plane that are all pairwise distinct, a “boomerang” is a tuple of points (i, j, k) such that the distance between i and j equals the distance between i and k (the order of the tuple matters).

Find the number of boomerangs. You may assume that n will be at most 500 and coordinates of points are all in the range [-10000, 10000] (inclusive).

Example:
Input: [[0,0],[1,0],[2,0]] Output: 2
Explanation: The two boomerangs are [[1,0],[0,0],[2,0]] and [[1,0],[2,0],[0,0]]

https://leetcode.com/problems/number-of-boomerangs
http://bit.ly/2x1PGxi

This is a permutation problem. 这道题定义了一种类似回旋镖形状的三元组结构,要求第一个点和第二个点之间的距离跟第一个点和第三个点之间的距离相等.现在给了我们n个点,让我们找出回旋镖的个数.那么我们想,如果我们有一个点a,还有两个点b和c,如果ab和ac之间的距离相等,那么就有两种排列方法abc和acb;如果有三个点b,c,d都分别和a之间的距离相等,那么有六种排列方法,abc, acb, acd, adc, abd, adb,那么是怎么算出来的呢,很简单,如果有n个点和a距离相等,那么排列方式为\(n(n-1)\),这属于最简单的排列permutation问题了,我大天朝中学生都会做的.那么我们问题就变成了遍历所有点,让每个点都做一次点a,然后遍历其他所有点,统计和a距离相等的点有多少个,然后分别带入n(n-1)计算结果并累加到res中,只有当n大于等于2时,res值才会真正增加.

struct Solution {
    int numberOfBoomerangs(vector<pair<int, int>>& points) {
        int r=0, L=points.size();
        for(int i=0;i<L;++i){
            map<int, int> m;
            for(int j=0;j<L;++j){
                if(i==j) continue;
                int x=points[i].first - points[j].first, y=points[i].second - points[j].second;
                m[x*x+y*y]++;
            }
            for(auto& pr: m)
                if(pr.second>=2) r+=pr.second*(pr.second-1);
        }
        return r;
    }
};

30.2 77. Combination (DFS)

https://leetcode.com/problems/combinations/

Time Complexity: \(O(K*C^{N}_{K})\)

N choose K

这道题的意思是从{1,2,3..n} 中找k-combination. CLRS P1185.

struct Solution {
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> r;
        vector<int> p, v(n);
        iota(v.begin(),v.end(),1);
        dfs(v,r,p,k,0);
        return r;
    }
    void dfs(const vector<int>& v,vector<vector<int>>& r,vector<int>& p,int k,int head){
        if (p.size()==k){r.push_back(p);return;} // 找到一个k-comb需要O(K)时间
        for(;head<v.size();head++){ // 注意这个循环和下面一题不同
            p.push_back(v[head]);
            dfs(v,r,p,k,head+1);
            p.pop_back();
        }
    }
};

坑是复杂度. 总共有N-choose-K个combinations,找到一个需要经历\(O(K)\).所以复杂度是他们的乘积.

K等于就是stack frame的深度.

30.3 17. Letter Combinations of a Phone Number

Given a digit string, return all possible letter combinations that the number could represent.

https://leetcode.com/problems/letter-combinations-of-a-phone-number

class Solution {
public:
    vector<string> letterCombinations(string d) {
        vector<string> r;
        string p;
        string m[] = {"", "", "abc", "def", "ghi", "jkl",
                      "mno", "pqrs", "tuv", "wxyz"};
        dfs(r, p, d, m, 0);
        return r;
    }
    // edge case: d="" --> [], d="111" --> [] !!!
    void dfs(vector<string>& r, string& p, string& d, string m[], int k){
        if(d.size()==k){ // Cannot use p!!!
            if(!p.empty()) r.push_back(p);
            return;
        }
        for(char c: m[d[k]-'0']){
            p+=c;
            dfs(r,p,d,m,k+1);
            p.pop_back();// backtrack in the graph, unwind the stack
        }
    }
};

难点是edge case导致的13行那个if condition.

30.4 Combination Sum I, II, III, IV

30.5 39. Combination Sum I

https://leetcode.com/problems/combination-sum/

Candidate number没有重复的情况,注意每个number可以重复使用,简单,直接DFS+Pruning.

struct Solution { // 49ms, 20%
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        vector<vector<int>> r;
        vector<int> p;
        sort(candidates.begin(),candidates.end()); //1
        dfs(r, p, target, candidates);
        return r;
    }
    void dfs(vector<vector<int>>& r, vector<int>& p, int t, vector<int>& candidates){
        if(t==0){ r.push_back(p); return;}// 终止条件
        else if(t<0) return;
        for(int i: candidates){
            if(!p.empty() && i>p.back()) continue; //can be backward or forward
            p.push_back(i);
            dfs(r,p,t-i,candidates);
            p.pop_back();
        }
    }
};

Q: sort的目的是什么? 不sort如何得到正确的结果?
A: 1. reduce search path. 2. remove dups
http://www.mitbbs.com/article_t/JobHunting/33249669.html

13行的大于号改成小于也是可行的.影响的只是combination里面的数字的顺序.

时间复杂度:

因为都是搜索题,所以搜索的时间复杂度是: O(解的个数 * 每个解生成的复杂度)

Combination sum这个题目因为有target存在所以并不知道解的个数,但是解的个数最多是子集的个数\(2^M\), 产生每个解的最坏复杂度是K(因为都是正数,我觉得K最坏的情况等于target),所以我们可以粗略的估计时间复杂度是\(O(K \cdot 2^M)\). M可以看下面的分析,我觉得最坏M等于target.

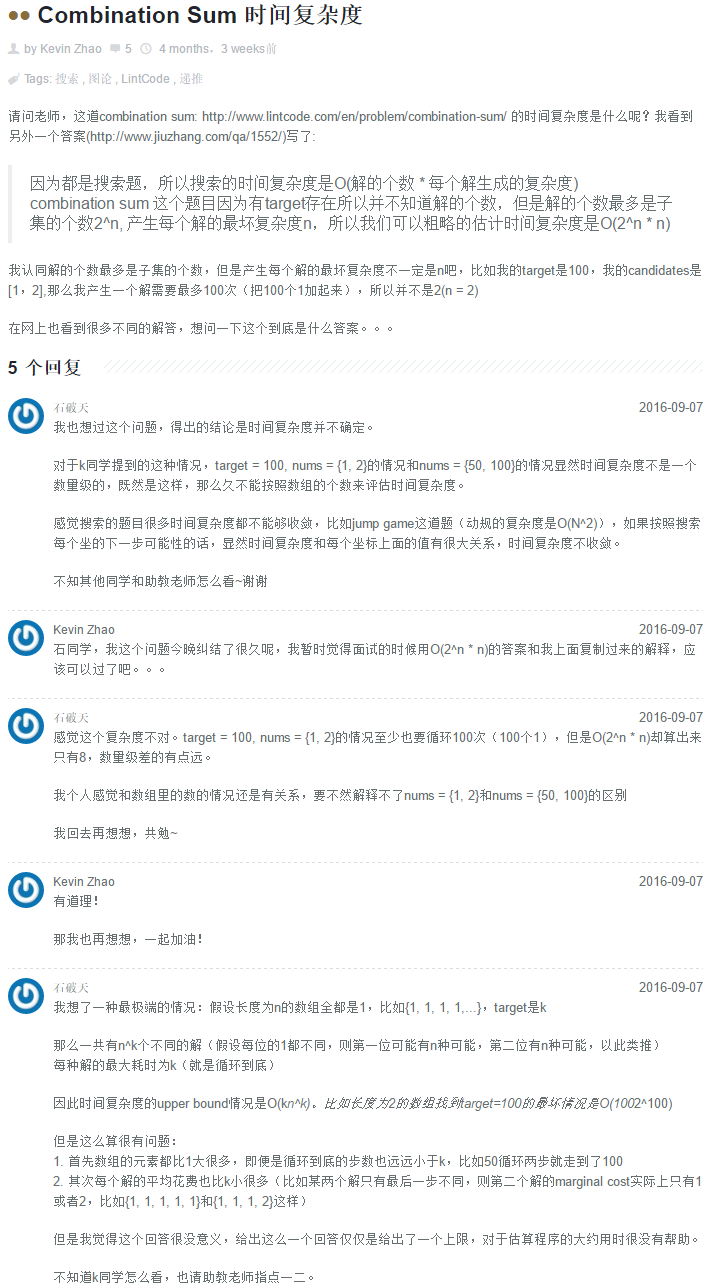
http://www.1point3acres.com/bbs/thread-123053-1-1.html
http://www.jiuzhang.com/qa/2088/
http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=206304

https://discuss.leetcode.com/topic/25900/if-asked-to-discuss-the-time-complexity-of-your-solution-what-would-you-say/8?show=62388

此题time complexity无比蛋疼
(1.) 首先来看Combination sum I和II的区别:
Combination sum 的input无dups, 但是input的元素可以重复利用
Combination sum II 的input有重复, 但是input的元素只能用一次

(2.) 其次, 弄明白 Combination sum II的time complexity是怎么一回事儿
https://github.com/Deadbeef-ECE/Interview/blob/master/Leetcode/BackTracking/040_Combination_Sum_II.java

\(O(k * 2^{M})\) time:
此题可以转换成 combination sum II, 如何做呢, 举个栗子:
int[] arr = {2, 3, 4, 5, 6}, target = 10;我们知道此题中,每个元素可以重复用,其实, 如果把 arr 变成 {2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6, 6}, 然后每个元素只能用一次, 就变成了combination sum II的要求了.

我们再看新数组, 元素多了很多. 多了多少? 那就是数组中所有小于等于target的元素E增加了ceil(target/E)个, 然后就可以用combination sum II的方法分析复杂度了. 这里M是新arr的大小

\(O(N)\) space:
One N is the recursion stack, another N is used when copying list.
Both of them depend on the longest solution which is equal to target/(min in candidates) in this problem(可以再看下上面的例子, n就是新arr中2的个数, 为ceil(10/2))

30.6 40. Combination Sum II

Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

Each number in C may only be used once in the combination.

Note:

All numbers (including target) will be positive integers. The solution set must not contain duplicate combinations.

For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8, A solution set is:

[
 [1, 7],
 [1, 2, 5],
 [2, 6],
 [1, 1, 6]
]

https://leetcode.com/problems/combination-sum-ii/

Candidate number有重复的情况,而且每个number只能用一次(和set那道题就有点像了),DFS + Remove Duplicates. 关键是同层不重复.

struct Solution {
  vector<vector<int>> combinationSum2(vector<int>& cs, int t) {
    vector<vector<int>> r;
    vector<int> p;
    vector<bool> vd(cs.size(), false);
    sort(cs.begin(), cs.end());
    dfs(r, p, cs, t, 0, vd);
    return r;
  }
  void dfs(vector<vector<int>>& r, vector<int>& p, 
    vector<int>& cs, int t, int head, vector<bool>& vd)
  {
    if (t == 0) { r.push_back(p); return; }
    if (t<0) return;
    for (int i = head; i<cs.size(); i++) {
      if (i>head && cs[i - 1] == cs[i] && !vd[i - 1]) continue;////
      //if(i>=1 && cs[i-1]==cs[i] && !vd[i-1]) continue;////
      //if(!p.empty() && p.back()>cs[i]) continue; // 因为一直往后走,可以省去
      vd[i] = true, p.push_back(cs[i]);
      dfs(r, p, cs, t - cs[i], i + 1, vd);
      vd[i] = false, p.pop_back();
    }
  }
};

这个才是最优的:

struct Solution { //19ms, 35%
    vector<vector<int>> combinationSum2(vector<int>& cs, int t) {
        vector<vector<int>> r;
        vector<int> p;
        sort(cs.begin(), cs.end());
        dfs(r,p,cs,t,0);
        return r;
    }
    void dfs(vector<vector<int>>& r,vector<int>& p,vector<int>& cs,int t,int head){
        if(t==0){r.push_back(p); return;}
        if(t<0) return;
        for(int i=head;i<cs.size();i++){
            if(i>head && cs[i-1]==cs[i]) continue;////
            p.push_back(cs[i]);
            dfs(r,p,cs,t-cs[i],i+1);
            p.pop_back();
        }
    }
};

因为循环一直往前,有head,所以往前走的就是没有访问过的,不需要visited bool vector

30.7 216. Combination Sum III

https://leetcode.com/problems/combination-sum-iii/

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

不需要去重,也没有重复数字,所以这题最简单.

这道题是个简化版的subset sum: https://en.wikipedia.org/wiki/Subset_sum_problem, which is a NP-complete problem. (CLRS 1128)

struct Solution {
    vector<vector<int>> combinationSum3(int k, int n) {
        vector<vector<int>> r;
        vector<int> p;
        dfs(r,p,k,n,1);
        return r;
    }
    void dfs(vector<vector<int>>& r, vector<int>& p, int k, int n, int head){
        if(k==0 && n==0){r.push_back(p); return;}
        if(k<0 || n<0) return;
        for(int i=head;i<=9;++i){
            p.push_back(i);
            dfs(r,p,k-1,n-i,i+1);// not head+1, it is i+1!!!
            p.pop_back();
        }
    }
};

30.8 377. Permutation Sum

Leetcode上的名字叫Combination Sum IV(Permutation Sum). 其实是个misnomer,应该叫做permutation sum IV.

https://leetcode.com/problems/combination-sum-iv/

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.

Example:

nums = [1, 2, 3]
target = 4

The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)

Note that different sequences are counted as different combinations.

Therefore the output is 7.

Follow up:

What if negative numbers are allowed in the given array?
How does it change the problem?
What limitation we need to add to the question to allow negative numbers?

https://www.hrwhisper.me/leetcode-combination-sum-iv/

题意:给定一个元素互不相同且均为正数的数组,让你用该数组中的数组合成target(可以重复使用),问有多少种.

思路1:DP

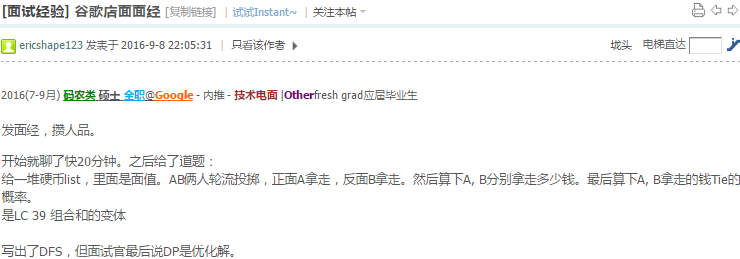
如果要算所有的路径,就必须用DFS.用[1,2,3], 4为例.绿色为叶子节点,我们看到有7个leaf nodes.

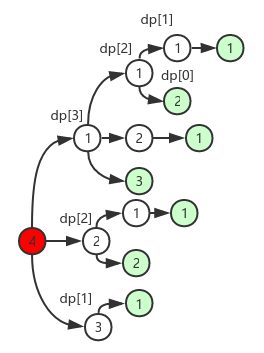
这道题给combination sum I非常接近,不过那道题是要找所有的路径.这里只求数目.

思路2:DP可以有两种写法(数学上是等价的)

\(dp[i] = \Sigma{dp[i-num]}\) (明显更容易想到)

dp[i+num] += dp[i]

这里dp[i]的定义是: 当candidates number给定的时候,并且target为i的时候,满足条件的permutation的个数.

和322 Coin Change那题差不多,不同的是Coin change求所有结果集合中最短的combination的长度.

假设给定的nums为\(num_1\), \(num_2\)…\(num_N\),用results[i]表示组成i的组合个数. 如果i >= \(num_j\), 那么

results[i] = results[i-num1]+results[i-num2]+...results[i-numj]

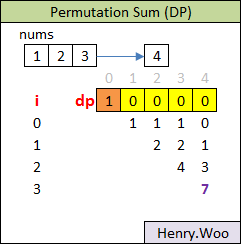
递推式写出来这道题其实只做出了一半,关键点是如何做loop.

在动态规划中,有状态转移方程,比如A状态转移到B状态,所以A状态可以转移到B状态的时候,A状态必须已经求出完毕了. 这道题目的状态转移方程式 dp[i] += dp[i - n] 那么我们求解i状态的时候,i - n状态必须求解完成,所以求解状态的顺序需要按照i从小到大枚举.如果for (int n : nums)循环放在外面,此时求解i状态,那么i-n状态是求解不完全的. 所以需要把i的循环放在最外层,这是一个动态规划求解状态的顺序.
https://www.jiuzhang.com/qa/1507/

• Algo 1 - Bottom Up

根据target来是正确的方法. 从0开始计算至target,就能获得target的排列(permutation)个数. 其实更像爬梯子的那道题Climbing Stairs.

struct Solution { // 3ms
  int combinationSum4(vector<int>& nums, int target) {
    vector<int> dp(target + 1, 0);
    dp[0] = 1;
    for (int i = 0; i < target; i++) ////
      for (int num : nums)
        if (i + num <= target) dp[i + num] += dp[i];
    return dp[target];
  }
};

参考: http://www.cnblogs.com/grandyang/p/5705750.html

• Algo 2 - Top Down

struct Solution { // 0ms
  int combinationSum4(vector<int>& nums, int target) {
    vector<int> dp(target + 1, 0);
    dp[0] = 1;
    for (int i = 1; i <= target; i++) ////
      for (int num : nums)
        if (i - num >= 0)
          dp[i] += dp[i - num];
    return dp[target];
  }
};

TopDown居然比BottomUp快了很多,because top-down just calculate necessary dp.

如果target远大于nums数组的个数的话([4,1,2],32,这个结果是39882198),上面的算法可以做适当的优化(复杂度不变),先给nums数组排个序,然后从1遍历到target,对于i小于数组中的数字x时,我们直接break掉,因为后面的数更大,其余地方不变. 参见代码如下:

struct Solution {
  int combinationSum4(vector<int>& nums, int target) {
    vector<int> dp(target + 1);
    dp[0] = 1;
    sort(nums.begin(), nums.end());
    for (int i = 1; i <= target; ++i) ////
      for (auto num : nums){
        if (i < num) break;
        dp[i] += dp[i - num];
      }
    return dp.back();
  }
};

如果有负数,可能产生循环,不限制使用元素次数和结果大小的话,可能造成加上减去相等的数无限循环.

http://xyma.me/2016/12/13/Combination-Sum-IV/
负数的出现导致的最大问题是无穷解.即由于负数的加入,导致可能某些数字的组合出现和为0,从而导致无限的0加入并不影响最终结果.

对于限制,如果正负Integer同时出现并且不限制数目的话,那么无法避免这中无限的情况.因为只要同时存在正负整数(a & b = -c),总可以找到a,c的公倍数导致 m x a + n x b = 0.

可能的限制是1. combination的长度, 2, 数字不可重复使用.比如下面这个例子就是第二种情况.

30.9 Combination Sum IV (Dup-Removing)

这才是真正的Combination Sum IV. Permutation去重不就是combination吗?

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=210190

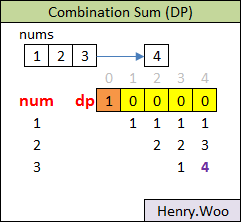
这道题在DP的同时注意去重.
上面那题是固定nums对target由小到大求解.这道题是一个个的加num求解.基本原理就是状态方程转移的时候,前面的状态需要求解完成.
首先对nums进行loop,以[1,2,3],4为例,假设candidate number只有1,那么dp[1~4]都是1,因为可以重复使用1; 然后如果2也是一个candidate,就把2放到combination result的最后,然后check dp[1],dp[1]不会受到影响,再check dp[2], dp[2]就会被影响,它需要自增dp[2-2]就是1,这样dp[2]=2;再check dp[3],dp[3]也要受影响,它要自增dp[3-2]=dp[1]=1;再check dp[4],当然也要受影响,它要自增dp[4-2]=dp[2]=2,所以dp[4]=3. 以此类推,得出下面的代码(其实只需要把上面两个for loop的顺序交换一下即可):

struct Solution {
  int combinationSum4(vector<int>& nums, int target) {
    vector<int> dp(target + 1, 0);
    dp[0] = 1;
    for (int num : nums)
      for (int i = 0; i < target; i++)
        if (i + num <= target) dp[i + num] += dp[i];
    return dp[target];
  }
};

30.10 518. Coin Change 2 (combination sum IV)

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.

Note: You can assume that

0 <= amount <= 5000 1 <= coin <= 5000 the number of coins is less than 500 the answer is guaranteed to fit into signed 32-bit integer

Example 1:

Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

Input: amount = 10, coins = [10] 
Output: 1

https://leetcode.com/problems/coin-change-2

struct Solution {
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1);
        dp[0]=1;
        for(int c: coins)
            for(int i=0; i<amount; ++i)
                if(i+c<=amount) dp[i+c] += dp[i];
        return dp.back();
    }
};

这题不能用Top down好像,只能用Bottom up.

30.11 322. Coin Change

https://leetcode.com/problems/coin-change/

https://www.hrwhisper.me/leetcode-coin-change/

You are given coins of different denominations and a total t of money t. Write a function to compute the fewest number of coins that you need to make up that t. If that t of money cannot be made up by any combination of the coins, return -1.

Example 1:
coins = [1, 2, 5], t = 11
return 3 (11 = 5 + 5 + 1)

Example 2:
coins = [2], t = 3
return -1.

零钱兑换,让你用最少的零钱数换取目标的数量.如有零钱1,2,5,换成11最少的为5+5+1 ,3个硬币
思路:
dp,设dp[i]为兑换目标i最少的硬币数.
则有:

dp[i + coins[j] ] = min(dp[i + coins[j] ] , dp[i] + 1)

或者

dp[i] = min(dp[i – coins[j]] + 1,dp[i])

说白了就是用当前的硬币能组合成啥,取最小.

struct Solution { // 29ms 65%
  int coinChange(vector<int>& coins, int t) {
    vector<int> dp(t + 1, INT_MAX);
    dp[0] = 0;
    for (int i = 0; i <= t; i++) { // 1
      for (int j = 0; j<coins.size(); j++) { // 2
        if (coins[j] != INT_MAX && i + coins[j] <= t &&
          dp[i] != INT_MAX && dp[i + coins[j]] > dp[i] + 1)
          dp[i + coins[j]] = dp[i] + 1;
      }
    }
    return dp[t] == INT_MAX ? -1 : dp[t];
  }
};

如果把第5,和第6行交换,permutation变combination,速度会更快

struct Solution { // 23ms, 90%
  int coinChange(vector<int>& coins, int t) {
    vector<int> dp(t + 1, INT_MAX);
    dp[0] = 0;
    for (int coin: coins) {
      for (int i = 0; i <= t; i++) {
        if (coin != INT_MAX && i + coin <= t &&
          dp[i] != INT_MAX && dp[i + coin] > dp[i] + 1)
          dp[i + coin] = dp[i] + 1;
      }
    }
    return dp[t] == INT_MAX ? -1 : dp[t];
  }
};

如果用-1来做特殊值,程序是这样的:

struct Solution { // 19ms, 95%
  int coinChange(vector<int>& coins, int t) {
    vector<int> dp(t + 1, -1);
    dp[0] = 0;
    for (int coin: coins)
      for (long i = 0; i <= t; ++i)
        if (i + coin <= t)
          if(dp[i]!=-1)
            if(dp[i + coin]<=0)
              dp[i + coin] = dp[i] + 1;
            else
              dp[i + coin] = min(dp[i] + 1,dp[i + coin]);
    return dp[t];
  }
};

复杂度: O(T x nums.size())

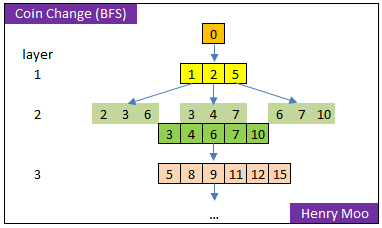
上面的空间复杂度都太高,最省空间的办法其实是BFS + vector for visited node tracking.

这里虽然是BFS,并没有使用queue,而是用的unordered_set. 因为下一层节点有重复节点.

struct Solution {
  int coinChange(vector<int>& coins, int t) {
    if(t<=0) return 0;
    unordered_set<long> F={0}, N;
    vector<bool> V(t);
    int cnt=0;
    while(!F.empty()){
        for(long i: F) //1
            for(int c: coins) //
                if(c+i<t && !V[c+i])
                    N.insert(c+i),V[c+i]=true;
                else if(c+i==t)
                    return ++cnt;
        F=N, N.clear(),++cnt;
    }
    return -1;
  }
};

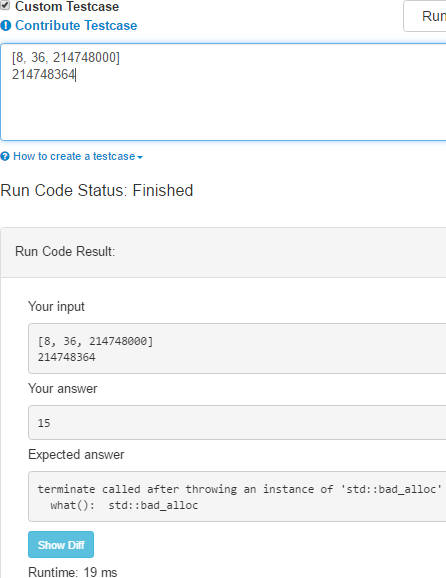
这个算法的空间复杂度经测试比Leetcode的解法好100倍.

---

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=201443

https://en.wikipedia.org/wiki/Subset_sum_problem

The easiest NP-hard problem: https://en.wikipedia.org/wiki/Partition_problem

https://en.wikipedia.org/wiki/Polynomial-time_approximation_scheme

http://wase.urz.uni-magdeburg.de/mertens/publications/npp5.pdf

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=206304

http://1point3acres.com/bbs/thread-200393-1-1.html

http://www.1point3acres.com/bbs/thread-177259-1-1.html

30.12 Permutation I. II

构造permutation的思路有至少如下三种:
- 插入法(iterative)
- 递归
- DFS图遍历

Time Complexity: \(O(N*N!)\)

30.13 Permutation I

Given a collection of distinct numbers, return all possible permutations.

For example, [1,2,3] have the following permutations:

[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]]

https://leetcode.com/problems/permutations/

http://bangbingsyb.blogspot.com/2014/11/leetcode-permutations-i-ii.html

Solution 1 - 插入法:

以题中例子说明:

当只有1时候:[1]
当加入2以后:[2, 1], [1, 2]
当加入3以后:
[3, 2, 1], [2, 3, 1], [2, 1, 3], 
[3, 1, 2], [1, 3, 2], [1, 2, 3]

前3个permutation分别对应将3插入[2, 1]的0, 1, 2的位置.同理后3个为插入[1, 2]的.因此可以用逐个插入数字来构造所有permutations.

struct Solution {
    vector<vector<int> > permute(vector<int> &num) {
        vector<vector<int>> allPer;
        if(num.empty()) return allPer;
        allPer.push_back(vector<int>(1,num[0]));
        for(int i=1; i<num.size(); i++) {
            int n = allPer.size();
            for(int j=0; j<n; j++) {
                for(int k=0; k<allPer[j].size(); k++) {
                    vector<int> per = allPer[j];
                    per.insert(per.begin()+k, num[i]);
                    allPer.push_back(per);
                }
                allPer[j].push_back(num[i]);
            }
        }
        return allPer;
    }
};

Solution 2 - 递归法:

比如perm(1,2,3),它等于

1 + perm(2,3)
2 + perm(1,3)
3 + perm(1,2)

所以这里需要把输入的vector依次删除一个char.自己写的,能过AC但效率不高:

vector<vector<int>> permute(vector<int>& nums) { // 29ms
    vector<vector<int>> r;
    if(nums.size()==1){
        r.push_back(nums);
        return r;
    }
    auto lambdafunc=[](vector<int> vi, int i){
        vector<int> r(vi);
        r.erase(r.begin()+i); // how to remove an item from vector
        return r;
    };
    for (int i=0; i<nums.size(); ++i){
        vector<int> tmp = lambdafunc(nums, i);
        auto pm = permute(tmp);// recursive
        for (auto p: pm){
          // to merge two vectors
          vector<int> first(1, nums[i]);
          first.insert(first.end(),p.begin(), p.end());
          r.push_back(first);
        }
    }
    return r;
}

Solution 3 - DFS:

和combination/subset不同,相同数字,不同的排列顺序,算作不同的permutation.所以我们需要用一个辅助数组来记录当前递归层时,哪些数字已经在上层的递归使用过了.

struct Solution { // 19ms
  vector<vector<int>> permute(vector<int>& nums) {
      vector<vector<int>> r;
      vector<int> p;
      vector<bool> vd(nums.size()); // visited
      dfs(nums,r,p,vd);
      return r;
  }
  void dfs(vector<int>& nums, vector<vector<int>>& r,
           vector<int>& p,vector<bool> vd)
  {
      if (p.size() == nums.size()){r.push_back(p); return;}
      for(int i=0; i<nums.size(); ++i){
          if (vd[i]) continue;
          vd[i]=true, p.push_back(nums[i]);// 前进的时候干活儿
          dfs(nums,r,p,vd);
          p.pop_back(), vd[i] = false;// backtrack的时候unwind
      }
  }
};

这里递归和DFS的区别显得特别清楚.

30.14 Permutation II

Given a collection of numbers that might contain duplicates, return all possible unique permutations.

For example, [1,1,2] have the following unique permutations:

[
 [1,1,2],
 [1,2,1],
 [2,1,1]
]

https://leetcode.com/problems/permutations-ii/

问题是去重.去重先要sort.

与I的区别在于有重复元素,所以在解集中要去重.思路和combination II, subset II的去重复基本一致.通过排序sort + 每层递归跳过重复数字.注意这里的重复数字指的是一直到当前递归层,还未被使用的数字中的重复.

• 递归

上面的思路没有任何问题,只是在实现起来,vector从后面插入更省事儿.所以就改动一下.

比如perm(1,2,3),它等于
perm(2,3)+1
perm(1,3)+2
perm(1,2)+3

而且这个去重排序之后很容易看出来.
perm(1,2,2,3) = perm(2,2,3)+1
perm(1,2,3)+2 //去重,当前面紧挨的那个数字和目前数字相同时 perm(2,2,2)+3

struct Solution { // 53ms
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        if (nums.size()==1){return vector<vector<int>>(1,nums);}
        auto f=[=](vector<int> vi, int i){vi.erase(vi.begin()+i); return vi;};
        vector<vector<int>> r;
        for (int i=0;i<nums.size();++i){
            if (i>=1 && nums[i]==nums[i-1]) continue;
            vector<int> nv = f(nums, i);
            auto tr = permuteUnique(nv);// tmp result
            for (auto& e: tr)
                e.push_back(nums[i]), r.emplace_back(e);
        }
        return r;
    }
};

• DFS

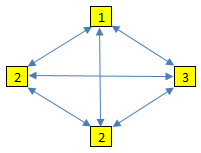
跟 Permutation I的解法一样,就是要考虑“去重”.先对数组进行排序,这样在DFS的时候,可以先判断前面的一个数是否和自己相等,相等的时候则前面的数必须使用了(说明是在DFS的上一层),自己才能使用,这样就不会产生重复的排列了.

struct Solution { // 33ms
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        vector<vector<int>> r;
        if (nums.empty()) return r;
        sort(nums.begin(), nums.end()); ////
        vector<int> p;
        vector<bool> vd(nums.size());// visited
        dfs(r,p,vd,nums);
        return r;
    }
    void dfs(vector<vector<int>>& r, vector<int>& p, 
             vector<bool>& vd,vector<int>& nums)
    {
        if(p.size() == nums.size()){ r.push_back(p); return; }
        for(int i=0;i<nums.size();i++){
            if(vd[i] or (i and nums[i]==nums[i-1] and !vd[i-1])) //1.去重
              continue;
            p.push_back(nums[i]), vd[i] = 1;
            dfs(r,p,vd,nums);
            p.pop_back(), vd[i] = 0;
        }
    }
};

在循环的时候去重和递归的方法相似.

1. 注意!vd[i-1]写成vd[i-1]也能过AC,这很难理解!!是对的.但vd[i-1]本身不能省去, or the inner recursion will skip using duplicate number(1223会变成13,长度永远达不到4,结果会为空).

30.15 60. Permutation Sequence

The set [1,2,3,…,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, We get the following sequence (ie, for n = 3):

"123"
"132"
"213"
"231"
"312"
"321"

Given n and k, return the kth permutation sequence.

https://leetcode.com/problems/permutation-sequence

class Solution {
    string x;
public:
    string getPermutation(int n, int k) {// kth n-perm
        string s(n,'0'); //
        iota(s.begin(),s.end(),'1');
        string p;
        vector<bool> vd(n);
        dfs(s,k,p,vd);
        return x;
    }
    void dfs(string s,int& k, string& p, vector<bool>& vd){
        if(!x.empty()) return;
        if(s.size()==p.size()){
            if(--k==0){ x=p; }
            return;
        }
        for(int i=0;i<s.size();i++){
            if(vd[i]) continue;
            vd[i]=true;
            p+=s[i];
            dfs(s,k,p,vd);
            p.pop_back();
            vd[i]=false;
        }
    }
};

这道题是让求出n个数字的第k个排列组合,由于其特殊性,我们不用将所有的排列组合的情况都求出来,然后返回其第k个,我们可以只求出第k个排列组合即可,那么难点就在于如何知道数字的排列顺序,可参见网友喜刷刷的博客,首先我们要知道当n = 3时,其排列组合共有3! = 6种,当n = 4时,其排列组合共有4! = 24种,我们就以n = 4, k = 17的情况来分析,所有排列组合情况如下:

1234
1243
1324
1342
1423
1432
2134
2143
2314
2341
2413
2431
3124
3142
3214
3241
3412 <--- k = 17
3421
4123
4132
4213
4231
4312
4321

我们可以发现,每一位上1,2,3,4分别都出现了6次,当第一位上的数字确定了,后面三位上每个数字都出现了2次,当第二位也确定了,后面的数字都只出现了1次,当第三位确定了,那么第四位上的数字也只能出现一次,那么下面我们来看k = 17这种情况的每位数字如何确定,由于k = 17是转化为数组下标为16:

最高位可取1,2,3,4中的一个,每个数字出现3!= 6次,所以k = 16的第一位数字的下标为16 / 6 = 2,即3被取出
第二位此时从1,2,4中取一个,k = 16是此时的k’ = 16 % (3!) = 4,而剩下的每个数字出现2!= 2次,所以第二数字的下标为4 / 2 = 2,即4被取出
第三位此时从1,2中去一个,k’ = 4是此时的k’’ = 4 % (2!) = 0,而剩下的每个数字出现1!= 1次,所以第三个数字的下标为 0 / 1 = 0,即1被取出
第四位是从2中取一个,k’’ = 0是此时的k’’’ = 0 % (1!) = 0,而剩下的每个数字出现0!= 1次,所以第四个数字的下标为0 / 1= 0,即2被取出

那么我们就可以找出规律了

a1 = k / (n - 1)!
k1 = k

a2 = k1 / (n - 2)!
k2 = k1 % (n - 2)!
...

an-1 = kn-2 / 1!
kn-1 = kn-2 / 1!

an = kn-1 / 0!
kn = kn-1 % 0! 

class Solution {
public:
    string getPermutation(int n, int k) {
        string res;
        string num = "123456789";
        vector<int> f(n, 1);
        for (int i = 1; i < n; ++i) f[i] = f[i - 1] * i;
        --k;
        for (int i = n; i >= 1; --i) {
            int j = k / f[i - 1];
            k %= f[i - 1];
            res.push_back(num[j]);
            num.erase(j, 1); // remove at index j
        }
        return res;
    }
};

• JAVA

public class Solution {
    public String getPermutation(int n, int k) {
        StringBuilder sb = new StringBuilder();
        ArrayList<Integer> num = new ArrayList<Integer>();
        int fact = 1;
        for (int i = 1; i <= n; i++) {
            fact *= i;
            num.add(i);
        }
        for (int i = 0, l = k - 1; i < n; i++) {
            fact /= (n - i);
            int index = (l / fact);
            sb.append(num.remove(index));
            l -= index * fact;
        }
        return sb.toString();
    }
}

30.16 Subsets/PowerSet (DAG DFS) I

https://leetcode.com/problems/subsets

https://en.wikipedia.org/wiki/Power_set

Subsets DFS is the most complicated DFS as the graph has every two points connecting with each other. As for the adjacency matrix, it is almost the most dense one, where all cell are 1 except diagonal cells. It is much more complicated than matrix, binary tree.

For binary tree, inside one \(dfs(\cdot)\), there are two recursive \(dfs(\cdot)\) calls because binary tree node has two children. The children number equals to the inner \(dfs(\cdot)\) calls number.

For subsets of \([a,b,c,d]\), inside one \(dfs(\cdot)\), if the current call site is at “a”, there are 3 \(dfs(\cdot)\) calls because “a” has three children; for “b”, the number becomes 2 as “b” has two children (“c” and “d”);

http://bangbingsyb.blogspot.com/2014/11/leetcode-subsets-i-ii.html

Note:

http://www.1point3acres.com/bbs/thread-117602-1-1.html

Time complexity is \(O(n*2^n)\), where n is the cardinality of the set. Space complexity is O(n).

Subset问题本质上是combination问题,求所有的１-combination, 2-combination,…K-combination. 在求combination的时候,下一个点的选择总是向一个方向前进.所以需要track当前起始点的位置(head).

30.16.1 DFS

• C++

// Runtime: 4 ms
struct Solution {
    vector<vector<int>> subsets(vector<int>& nums) {
        //sort(nums.begin(), nums.end());
        vector<vector<int>> r;
        vector<int> p;
        dfs(nums, r, p , 0);
        return r;
    }
    void dfs(vector<int>& nums, vector<vector<int>>& r, vector<int>& p, int head){
        r.push_back(p);
        for (; head<nums.size(); ++head){
            p.push_back(nums[head]);
            dfs(nums, r, p, head+1);////!!!!
            p.pop_back();
        }
    }
};

• Python

class Solution(object):
    def subsets(self, nums):
        r, p =[], []
        self.dfs(nums, r, p, 0)
        return r
    def dfs(self, nums, r, p, head):
        r.append(list(p))####
        for i in range(head, len(nums)):
            p.append(nums[i])
            self.dfs(nums, r, p, i+1)
            p.pop()

https://stackoverflow.com/questions/13299427/python-functions-call-by-reference

• Java

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> r = new ArrayList<>(); //?
        List<Integer> p = new ArrayList<Integer>();
        dfs(nums, r, p, 0);
        return r;
    }
    public void dfs(int[] nums, List<List<Integer>> r, List<Integer> p, int head){
        r.add(new ArrayList<Integer>(p));
        for(int i=head; i<nums.length; ++i){
            p.add(nums[i]);
            dfs(nums, r, p, i+1);
            p.remove(p.size() - 1); //?
        }
    }
}

https://www.javaworld.com/article/2077424/learn-java/does-java-pass-by-reference-or-pass-by-value.html
https://stackoverflow.com/questions/9852831/polymorphism-why-use-list-list-new-arraylist-instead-of-arraylist-list-n

30.16.2 Recursion

struct Solution {
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> r(1,vector<int>());
        if(nums.empty()){return r;}
        if(nums.size()==1){r.push_back(nums); return r;}
        //Elements in a subset must be in non-descending order
        sort(nums.begin(),nums.end());
        int bak = nums.back();
        nums.pop_back();
        vector<vector<int>> t = subsets(nums);// Recursion
        vector<vector<int>> t2(1, vector<int>(1, bak));

        for (int i=0;i<t.size();++i){
            if (!t[i].empty()){
                vector<int> v(t[i]);
                v.push_back(bak);
                t2.push_back(v);
            }
        }
        t.insert(t.end(),t2.begin(),t2.end());
        return t;
    }
};

Version 2:

struct Solution {
    vector<vector<int>> subsets(vector<int> &S) {
        vector<vector<int>> allSets;
        vector<int> sol;
        allSets.push_back(sol);
        sort(S.begin(), S.end());
        for(int i=0; i<S.size(); i++) {
            int n = allSets.size();
            for(int j=0; j<n; j++) {
                sol = allSets[j];
                sol.push_back(S[i]);
                allSets.push_back(sol);
            }
        }
        return allSets;
    }
};

30.16.3 Bit manipulation

// Runtime: 8 ms
struct Solution {
    vector<vector<int>> subsets(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int L = nums.size(), N = 1<<L;
        vector<vector<int>> r;
        auto f=[&nums](int i){
            vector<int> r;
            for(int j=0; i!=0; i>>=1, ++j)
                if(i&1) r.push_back(nums[j]);
            return r;
        };
        for(int i=0; i<N; ++i)
            r.push_back(f(i));
        return r;
    }
};

30.17 Subsets/PowerSet (DAG DFS) II

https://leetcode.com/problems/subsets-ii

Given a collection of integers that might contain duplicates, nums, return all possible subsets.

Note: The solution set must not contain duplicate subsets.

难点是去重,所以可以直接用subset I的方法用unordered_set来去重.

class Solution { // 16ms
//对每一个节点做前向的DFS
//这道题level和partial_solution的长度不同,必须同时有
//不像word search那道题
public:
    using VVI = vector<vector<int>>;
    using SVI = unordered_set<vector<int>>;
    using VI = vector<int>;
    void dfs(VI& nums, SVI& r, int level, VI& p){
        r.insert(p);
        for (; level<nums.size(); ++level){
            p.emplace_back(nums[level]);
            dfs(nums, r, level+1, p);
            p.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        SVI r;
        VI p;
        for (int i=0; i<nums.size(); ++i)
            dfs(nums, r, i, p);
        VVI r2;
        for (auto x:r){r2.push_back(x);}
        return r2;
    }
};

这个是标准的解法:

class Solution { // 9ms
public:
    using VVI = vector<vector<int>>;
    using SVI = set<vector<int>>;
    using VI = vector<int>;
    void dfs(VI& nums, VVI& r, int level, VI& p){
        r.push_back(p);
        for (int i=level; i<nums.size(); ++i){
            if(i>level && nums[i]==nums[i-1]) continue;////
            p.emplace_back(nums[i]);
            dfs(nums, r, i+1, p);
            p.pop_back();
        }
    }
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        VVI r;
        VI p;
        dfs(nums, r, 0, p);
        return r;
    }
};

30.18 Subset Sum

30.19 634. Find the Derangement of An Array

In combinatorial mathematics, a derangement is a permutation of the elements of a set, such that no element appears in its original position.

There’s originally an array consisting of n integers from 1 to n in ascending order, you need to find the number of derangement it can generate.

Also, since the answer may be very large, you should return the output mod 109 + 7.

Example 1:

Input: 3
Output: 2
Explanation: The original array is [1,2,3]. The two derangements are [2,3,1] and [3,1,2].

Note: n is in the range of [1, \(10^6\)].

https://leetcode.com/problems/find-the-derangement-of-an-array https://en.wikipedia.org/wiki/Derangement

http://bookshadow.com/weblog/2017/07/02/leetcode-find-the-derangement-of-an-array/

公式推导过程可以参考:https://en.wikipedia.org/wiki/Derangement

错位排列可以理解成将标号为1-n的帽子分配给标号为1-n的人,每个人拿到的帽子标号都与其自身的标号不同.

假设第一个人选取了标号为i的帽子,此时可分两种情况讨论:

1. 第i个人选择第一顶帽子,则问题规模缩小为n - 2

   2, 3, 4, …, i-1, i+1, … n 人
   2, 3, 4, …, i-1, i+1, … n 帽

2. 第i个人不选第一顶帽子,则问题规模缩小为n - 1(相当于第i个人不能选择第1顶帽子)

   2, 3, 4, …, i-1, i, i+1, …, n 人
   2, 3, 4, …, i-1, 1, i+1, …, n 帽

Suppose that there are n people who are numbered 1, 2, …, n. Let there be n hats also numbered 1, 2, …, n. We have to find the number of ways in which no one gets the hat having same number as their number. Let us assume that the first person takes hat i. There are n − 1 ways for the first person to make such a choice. There are now two possibilities, depending on whether or not person i takes hat 1 in return:

Person i does not take the hat 1. This case is equivalent to solving the problem with n − 1 persons and n − 1 hats: each of the remaining n − 1 people has precisely 1 forbidden choice from among the remaining n − 1 hats (i’s forbidden choice is hat 1).

Person i takes the hat 1. Now the problem reduces to n − 2 persons and n − 2 hats.

From this, the following relation is derived:

!n = ( n − 1 ) ( !( n − 1 ) + !( n − 2 ) )

where !n, known as the subfactorial, represents the number of derangements, with the starting values !0 = 1 and !1 = 0.

递推式:

dp[n] = (dp[n - 1] + dp[n - 2]) * (n - 1)

struct Solution {
    int findDerangement(int n) {
        // recursion: !n = (n-1) * (!(n-1) + !(n-2)); base case: n is 1 or 2
        if (n == 1) return 0;
        if (n == 2) return 1;
        unsigned long long int a=0, b=1, c=0; // at least 64bits
        int k=3;
        while (k <= n) // a, b, c
            c = (k++ - 1) * (b + a) % 1000000007, a = b, b = c;
        return c;
    }
};

30.20 629. K Inverse Pairs Array

Given two integers n and k, find how many different arrays consist of numbers from 1 to n such that there are exactly k inverse pairs.

We define an inverse pair as following: For ith and jth element in the array, if i < j and a[i] > a[j] then it’s an inverse pair; Otherwise, it’s not.

Since the answer may be very large, the answer should be modulo \(10^9 + 7\).

Example 1:

Input: n = 3, k = 0
Output: 1
Explanation: 
Only the array [1,2,3] which consists of numbers from 1 to 3 has exactly 0 inverse pair.

Example 2:

Input: n = 3, k = 1
Output: 2
Explanation: 
The array [1,3,2] and [2,1,3] have exactly 1 inverse pair.

Note:

The integer n is in the range [1, 1000] and k is in the range [0, 1000].

https://leetcode.com/problems/k-inverse-pairs-array/

我们需要一个二维的DP数组,其中dp[i][j]表示1到i的数字中有j个翻转对的排列总数,那么我们要求的就是dp[n][k]了,即1到n的数字中有k个翻转对的排列总数.现在难点就是要求递推公式了.我们想如果我们已经知道dp[n][k]了,怎么求dp[n+1][k],先来看dp[n+1][k]的含义,是1到n+1点数字中有k个翻转对的个数,那么实际上在1到n的数字中的某个位置加上了n+1这个数,为了简单起见,我们先让n=4,那么实际上相当于要在某个位置加上5,那么加5的位置就有如下几种情况:

xxxx5
xxx5x
xx5xx
x5xxx
5xxxx

这里xxxx表示1到4的任意排列,那么第一种情况xxxx5不会增加任何新的翻转对,因为xxxx中没有比5大的数字,而 xxx5x会新增加1个翻转对,xx5xx,x5xxx,5xxxx分别会增加2,3,4个翻转对.

xxxx5相当于dp[n][k],即dp[4][k],那么依次往前类推,就是dp[n][k-1], dp[n][k-2]…dp[n][k-n],这样我们就可以得出dp[n+1][k]的求法了:

dp[n+1][k] = dp[n][k] + dp[n][k-1] + ... + dp[n][k - n]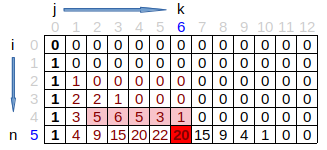

struct Solution {
  int kInversePairs(int n, int k) {
    vector<vector<long long>> dp(n+1, vector<long long>(k+1));
    for(int i=1;i<=n;++i) dp[i][0]=1;
    for(int i=2;i<=n;++i)
      for(int j=1;j<=k;++j){
        if(j>2 && dp[i][j-1]==1) break;
        for(int m=0; m<i; m++)
          if(j < m) break; else dp[i][j] += dp[i-1][j-m];
        dp[i][j] %= 1000000007;
      }
    return dp[n][k];
  }
};

很明显这题可以用滚动数组完成减少Space complexity.略.

这个矩阵和Pascal triangle非常相似,也是具有对称性,也是被1从两边包围.奇妙!

30.21 790. Domino and Tromino Tiling

We have two types of tiles: a 2x1 domino shape, and an “L” tromino shape. These shapes may be rotated.

XX  <- domino

XX  <- "L" tromino
X

Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.

(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)

Example:
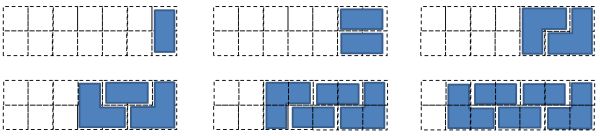
Input: 3
Output: 5
Explanation:
The five different ways are listed below, different letters indicates different tiles:

XYZ XXZ XYY XXY XYY
XYZ YYZ XZZ XYY XXY

https://leetcode.com/problems/domino-and-tromino-tiling/

https://cs.stackexchange.com/questions/66658/domino-and-tromino-combined-tiling

class Solution {
public:
    int numTilings(int N) {
        m[1]=1, m[2]=2, m[3]=5;
        return dp(N);
    }
    long long dp(int n){
        if(m[n]) return m[n];
        long long s=2*dp(n-1) + dp(n-3);
        return m[n]=s%1000000007;
    }
    long long m[1000]={};
};

Recursions formula: \(f(n)=2f(n-1)+f(n-3)\)

For domino only, formula is \(f(n)=f(n-1)+f(n-2)\)