Chapter 23 Math & Probability

23.1 Reverse Integer

https://leetcode.com/problems/reverse-integer/

Test cases:

10 -> 1
-123 -> -321
0 -> 0
123->321
INT_MAX -> 0
INT_MIN -> 0

This piece of code can deal with all the test cases above:

int reverse(int x) {
  long long r=0;
  while(x) r = r*10 + x%10, x /= 10;
  return (r>INT_MAX || r<INT_MIN) ? 0 : r; //int overflow check
}

If long long is not allowed, we can use this:

int reverse(int x){
  int r = 0, p = 0;
  while(x){
    p = r, r = r*10 + x%10;
    if (r/10!=p) return 0; //int overflow check
    x /= 10;
  }
  return r;
}

Python has different modulo result from C++, so you need to use abs function. Python Version:

class Solution(object):
    def reverse(self, x):
        r, y = 0, abs(x)
        while y:
            r, y = r*10 + y%10, y/10
        return r*(2*(x>0)-1) if r<=(2**31-1) else 0

23.2 313. Super Ugly Number

Write a program to find the nth super ugly number.

Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of size k. For example, [1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32] is the sequence of the first 12 super ugly numbers given primes = [2, 7, 13, 19] of size 4.

Note: (1) 1 is a super ugly number for any given primes. (2) The given numbers in primes are in ascending order. (3) 0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000.

https://leetcode.com/problems/super-ugly-number/

google-2016-12.html#ugly-number-iii-super-ugly-number

23.3 326. Power of Three

https://leetcode.com/problems/power-of-three/

http://www.cnblogs.com/grandyang/p/5138212.html

bool isPowerOfThree(int n) {
        //return (n > 0 && int(log10(n) / log10(3)) - log10(n) / log10(3) == 0);
        return n > 0 && (1162261467 % n == 0);
}

23.4 Biased Random Generator

http://bit.ly/2gRl1PA

这样行吗,取一个数k = ceil(log2(n)),扔k次,把这k次的结果看成一个binary number,这个数小于等于n-1的概率是n/(2^k),反复投掷知道这个数小于等于n-1为止,然后再看这个数是否等于0. 证明就是楼上说的条件概率吧.

如果投掷k次,把每次投掷的结果看作0或1(正或反),那么投k次的结果就可以用一个k位的二进制数表示,这样会得到2^k个数,而且得到每个数的概率是一样的.但是题目要求模拟1/n的概率,所以就要设法以均匀的概率产生n个数,那么产生其中一个数的概率就是1/n.

这个方法就是,选一个k使得2^k >= n.然后这样模拟1/n概率: 1. 投掷k次,产生一个数m,范围是0～2^k - 1 2. 如果0 =< m <= n - 1, 停止投掷,跳到3.否则跳回1 3. m等于[0, n - 1]其中任意一个数的概率就是1/n.

23.5 Weighted Random Number Generator

http://www.1point3acres.com/bbs/thread-168330-1-1.html

大概就是一个数组1,4,2,6…. 每次调用一个函数,按照数组里面的数字的大小,返回相应的Index. 比如, 上面的例子就是. 1/13 的概率返回0, 4/13的概率返回1. 说了两个办法,一个累加起来, 然后用一个随即数,看看在哪个范围里面.另一个先加好,然后Binary search,让写了第二个.

23.6 Probability key from a given map

Return a probability key from a given map, e.g. map<String, Integer> contains Apple 10, Orange 20, then the method 三分之一的概率返回苹果,三分之二返回橘子. http://bit.ly/2gPLZXU

Put them into array or BST(map) and use binary search/lower_bound.

T: \(O(LogN)\)

string getprobkey(map<string, int>& m){
  map<int,string> cm; //cumulative map
  int cs=0; //cumulative sum
  for(auto pr: m)
    cm[cs+=pr.second] = pr.first;
  int t=rand()%p+1;
  return cm.lower_bound(t)->second;
}

23.7 Two Sigma - Random weighted string

Given many (string, weight(int)) pairs, return string with probability proportional to its weight. Also we can set(string, weight), when weight eqaul to 0, remove the string.

#include <henry.h>
struct A{
  map<string, int> m; // string to index
  vector<pair<int,string>> v; // cumulative weight to string
  A(){srand(time(0));}
  string get(){               // O(N)
    int n=v.back().first;
    int k=rand()%n;
    int l=0;
    for(auto pr: v)
      if(l<= k and k<pr.first) return pr.second; else l=pr.first;
    return ""; 
  }
  void set(string s, int w){  // O(N)
    if(v.empty()){
      m[s]=0;
      v.emplace_back(w, s); 
    }else{
      if(m.count(s)){
        int i=m[s];
        int delta=w - (v[i].first-(i>0?v[i-1].first:0));
        for(;i<v.size();++i){
          v[i].first+=delta;
        }
      }else{
        v.emplace_back(v.back().first+w, s); 
        m[s]=v.size()-1;
      }   
    }   
  }
};
int main(){
  A a;
  a.set("a",10);
  a.set("b",20);
  a.set("c",30);
  a.set("d",40);
  map<string, int> c;
  int k=1000;
  while(k--) c[a.get()]++;
  for(auto pr: c) cout << pr.first << " - " << pr.second << endl;
  a.set("a",40);
  a.set("b",30);
  a.set("c",10);
  a.set("d",20);
  c.clear();
  k=1000;
  while(k--) c[a.get()]++;
  for(auto pr: c) cout << pr.first << " - " << pr.second << endl;
  return 0;
}

Improve:

#include <henry.h>
struct A{
  map<string,int> m;  // string to index
  vector<int> vi;     // cumulative weight
  vector<string> vs;  // strings
  A(){srand(time(0));}
  string get(){
    int n=vi.back();
    int k=rand()%n;
    int i=upper_bound(vi.begin(), vi.end(), k)-vi.begin(); // LogN
    return vs[i];
  }
  void set(string s, int w){ //O(N)
    if(vi.empty()){
      m[s]=0;
      vi.push_back(w), vs.push_back(s);
    }else{
      if(m.count(s)){
        int i=m[s];
        int delta=w - (vi[i]-(i>0?vi[i-1]:0));
        for(;i<vi.size();++i){
          vi[i]+=delta;
        }
      }else{
        vi.push_back(vi.back()+w), vs.push_back(s);
        m[s]=vi.size()-1;
      }   
    }   
  }
};
int main(){
  A a;
  a.set("a",10);
  a.set("b",20);
  a.set("c",30);
  a.set("d",40);
  map<string, int> c;
  int k=1000;
  while(k--) c[a.get()]++;
  for(auto pr: c) cout << pr.first << " - " << pr.second << endl;
  a.set("a",40);
  a.set("b",30);
  a.set("c",10);
  a.set("d",20);
  c.clear();
  k=1000;
  while(k--) c[a.get()]++;
  for(auto pr: c) cout << pr.first << " - " << pr.second << endl;
  return 0;
}

23.8 537. Complex Number Multiplication

Input: "1+1i", "1+1i"
Output: "0+2i"
Explanation: (1 + i) * (1 + i) = 1 + i2 + 2 * i = 2i, and you need convert it to the form of 0+2i.
Example 2:
Input: "1+-1i", "1+-1i"
Output: "0+-2i"
Explanation: (1 - i) * (1 - i) = 1 + i2 - 2 * i = -2i, and you need convert it to the form of 0+-2i.

https://leetcode.com/problems/complex-number-multiplication/
http://www.cnblogs.com/grandyang/p/6660437.html

下面这种方法利用到了字符串流类istringstream来读入字符串,直接将实部虚部读入int变量中,注意中间也要把加号读入char变量中,然后再进行运算即可,参见代码如下:

struct Solution {
    string complexNumberMultiply(string a, string b) {
        istringstream is1(a), is2(b);
        int a1, a2, b1, b2, r1, r2;
        char plus;
        is1 >> a1 >> plus >> a2;
        is2 >> b1 >> plus >> b2;
        r1 = a1 * b1 - a2 * b2, r2 = a1 * b2 + b1 * a2;
        return to_string(r1) + "+" + to_string(r2) + "i";
    }
};

23.9 Coupon collector’s problem

2016(1-3月) 码农类硕士全职Google - 内推 - HR筛选 |Other其他
google常考题,大家有思路吗?
you have 1 meter walkroad, and randomly generate rain, the rain is 1 cm. simulate how many rain drops to cover all the 1 meter [-0.01~1].

http://www.1point3acres.com/bbs/thread-176388-1-1.html

Follow up: time complexity? NLogN

https://en.wikipedia.org/wiki/Coupon_collector%27s_problem

int rand (void);

Generate random number
Returns a pseudo-random integral number in the range between 0 and RAND_MAX.

This number is generated by an algorithm that returns a sequence of apparently non-related numbers each time it is called. This algorithm uses a seed to generate the series, which should be initialized to some distinctive value using function srand.

RAND_MAX is a constant defined in <cstdlib>. 不同的库具体值不同. Windows 32768, Linux INT_MAX.

Notice though that this modulo operation does not generate uniformly distributed random numbers in the span (since in most cases this operation makes lower numbers slightly more likely).

23.9.1 Algo: Total covered length of adding interval

Get total covered length

struct raindrop{
    list<pair<double, double>> l;
    const double RAIN_LEN=0.01;
    const pair<double,double> ROAD{-0.01,1};
    double sz=0.0;
    bool fullycovered(){ return sz>=1.0; /*return abs(sz-1.0)<1e-10;*/ }
    bool drop(double start, double end){
        bool merged=false;
        list<pair<double, double>>::iterator it=l.begin();
        while(it != l.end()){
            if(it->first > end){
                if(!merged){
                    l.insert(it,{start, end});
                    sz += end-start;
                    merged=true;
                    break;
                }else{}
            }else if(it->second<start){
            }else{ // overlap
                start=min(start,it->first), end=max(end, it->second);
                sz -= (it->second - it->first);
                it = l.erase(it);
                continue;
            }
            ++it;
        }
        if(!merged){
            sz += end-start;
            l.push_back({start, end});
        }
        return fullycovered();
    }
    // >>> math.log(101)* 101 == 466.1271722009672
    int simulate(){
        srand(time(NULL));
        int r=0;
        double start;
        do{
            r++;
            // be careful start should be {-0.01, 1-0.01=0.99}
            start = (rand()%101 -1)/100.0;// generate x=(0-100) then (x-1)/100.0
        }while(!drop(start, start+RAIN_LEN));
        return r;
    }
};

23.10 625. Minimum Factorization

Given a positive integer a, find the smallest positive integer b whose multiplication of each digit equals to a.

If there is no answer or the answer is not fit in 32-bit signed integer, then return 0.

Example 1
Input: 48 Output: 68

Example 2
Input: 15 Output: 35

https://leetcode.com/problems/minimum-factorization

这道题和factor combination looks very similar at the first glance, but the algo is totally different. 这也是告诉我们面试的时候乱套题是不行的;-)

简单描述一下题目,给定一个正整数,找到一个最小的正整数,使得该最小正整数的各位乘积等于上述给定的正整数,如果这个数超过32位int的表示范围,就返回0.

这题其实很简单的,但没做出来确实罪过.首先,各位的乘积,就表示不可能出现超过1位的数,然后考虑最小,如果数最小,那么就一定是小的数的乘积在前面,只需要从9开始不断地对原数做除法,迭代递减至2就可以了,这样就一定保证了最小的乘积在最前面,如果最后的余数大于9,那就证明不存在这样的解,直接return 0.

还有一点,从得到的乘积恢复成数的过程中,判断是不是int溢出其实很简单,在C++里定义一个long,可以存储大于INT_MAX的值,直接判断就OK.这个技巧可以用在很多类似的判断是否溢出的题目中.

struct Solution {
    int smallestFactorization(int a) { //
        if (a < 2) return a;
        long long int l = 0, r=0;
        for (int i = 9; i >= 2; i--) {
            while (a % i == 0) ////
                l = l*10 + i, a /= i;
        }
        if(a!=1) return 0;
        while(l) r=r*10+l%10, l/=10;
        return r>INT_MAX ? 0 : r;
    }
};

这题关键点是从9到2开始循环除,还有就是对int overflow的处理. 有多种implementation的情况主要在于如何处理先得到的大数放在LSB位置,而小数放在MSB. 比如:

struct Solution {
    int smallestFactorization(int a) { //
        if (a < 10) return a;
        long long int r = 0, mag=1;
        for (int i = 9; i >= 2; i--)
            while (a % i == 0) ////
                r += mag*i, a /= i, mag*=10;
        return a!=1 || r>INT_MAX ? 0 : r;
    }
};

23.11 398. Random Pick Index

Given an array of integers with possible duplicates, randomly output the index of a given target number. You can assume that the given target number must exist in the array.
Note: The array size can be very large. Solution that uses too much extra space will not pass the judge.
Example:

int[] nums = new int[] {1,2,3,3,3};
Solution solution = new Solution(nums);
// pick(3) should return either index 2, 3, or 4 randomly.
// Each index should have equal probability of returning.
solution.pick(3);
// pick(1) should return 0. Since in the array only nums[0] is equal to 1.
solution.pick(1);

https://leetcode.com/problems/random-pick-index
http://www.cnblogs.com/grandyang/p/5875509.html

这题考蓄水池抽样

struct Solution {
    vector<int> v;
    Solution(vector<int> nums):v(nums){}
    int pick(int t) {
        int r=0, c=1;
        for(int i=0;i<v.size();++i)
            if(v[i]==t && rand()%c++==0) r=i;
        return r;
    }
};

23.12 483. Smallest Good Base

For an integer n, we call k>=2 a good base of n, if all digits of n base k are 1.

Now given a string representing n, you should return the smallest good base of n in string format.

Example 1:

Input: “13”
Output: “3”
Explanation: 13 base 3 is 111.

Example 2:

Input: “4681”
Output: “8”
Explanation: 4681 base 8 is 11111.

Example 3:

Input: “1000000000000000000”
Output: “999999999999999999”
Explanation: 1000000000000000000 base 999999999999999999 is 11.

https://leetcode.com/problems/smallest-good-base

http://bit.ly/2wHCflO

23.13 357. Count Numbers with Unique Digits

Given a non-negative integer n, count all numbers with unique digits, x, where 0 <= x < 10^n.

Example: Given n = 2, return 91. (The answer should be the total numbers in the range of 0 <= x < 100, excluding [11,22,33,44,55,66,77,88,99])

https://leetcode.com/problems/count-numbers-with-unique-digits

Combinatorics + DP

Count Numbers with Unique Digits

http://bit.ly/2vNRlb4

struct Solution {
    int countNumbersWithUniqueDigits(int n) { // until n
        if(n>9 || n<0) return 0;
        if(n==0) return 1; // edge case of n=0
        vector<int> dp(n+1);
        dp[1]=10;
        return rec(dp,n);
    }
    int rec(vector<int>& dp, int n){
        if(dp[n]) return dp[n];
        int start=9, r=start, k=n-1;
        while(k--)
            r *= start--;
        return dp[n]=(r+rec(dp,n-1));
    }
};

23.14 172. Factorial Trailing Zeroes

Given an integer n, return the number of trailing zeroes in n!. Note: Your solution should be in logarithmic time complexity.

https://leetcode.com/problems/factorial-trailing-zeroes

int trailingZeroes(int n) { return n<=4 ? 0 : n/5+trailingZeroes(n/5); }

是让求一个数的阶乘末尾0的个数,也就是要找乘数中10的个数,而10可分解为2和5,而我们可知2的数量又远大于5的数量,那么此题即便为找出5的个数.仍需注意的一点就是,像25,125,这样的不只含有一个5的数字需要考虑进去.

public class Solution {
    public int trailingZeroes(int n) {
        int res = 0;
        while (n > 0) {
            res += n / 5;
            n /= 5;
        }
        return res;
    }
}

Another Trailing Zeroes asked in interview with Wish.com:

//trailingZero
//int -> int
// 100 -> 2
// 203 -> 0
// O(N)
int f(int i){
    if(i==0) return 1;
    int r=0;
    while(i){
        if(i%10==0) r++; else return r;
        i/=10;
    }
    return r;
}
#include <math.h>
int f2(long long int i, int L=40){ // 20
    if(i==0) return 1;
    int l=0, r=L-1;
    while(l<=r){
        int m=l+(r-l)/2;
        int base = pow(10,m);
        if(i%base==0) //!!
            l=m+1;
        else r=m-1;
    }
    return r;
}

23.15 319. Bulb Switcher

There are n bulbs that are initially off. You first turn on all the bulbs. Then, you turn off every second bulb. On the third round, you toggle every third bulb (turning on if it’s off or turning off if it’s on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb. Find how many bulbs are on after n rounds.

Example:
Given n = 3. 
At first, the three bulbs are [off, off, off].
After first round, the three bulbs are [on, on, on].
After second round, the three bulbs are [on, off, on].
After third round, the three bulbs are [on, off, off]. 
So you should return 1, because there is only one bulb is on.

https://leetcode.com/problems/bulb-switcher/

struct Solution { int bulbSwitch(int n) { return sqrt(n);} };

2016(4-6月) 码农类硕士全职 Linkedin - 猎头 - 技术电面 |Other在职跳槽
1. 有n个学生(编号为sid = [1..n])依次走进有n个锁柜的房间(锁的编号为lockid = [1..n]),该学生将会打开或锁上lockid可以被sid整除的锁,写一个打印所有在第n个学生操作后处于打开的状态的lockid.2. Shortest Word Distance II,需要处理word1和word2相同的情况,并需要注意该情况下list中只有一个word1的case. http://bit.ly/2iRb0T5

23.16 672. Bulb Switcher II

There is a room with n lights which are turned on initially and 4 buttons on the wall. After performing exactly m unknown operations towards buttons, you need to return how many different kinds of status of the n lights could be.

Suppose n lights are labeled as number [1, 2, 3 …, n], function of these 4 buttons are given below:

1.Flip all the lights.
2.Flip lights with even numbers.
3.Flip lights with odd numbers.
4.Flip lights with (3k + 1) numbers, k = 0, 1, 2, ...

https://leetcode.com/problems/bulb-switcher-ii

When n <= 1, the solution is trivial.

From the 4 types of operations, there are three important observations:
1. For any operation, only odd or even matters, i.e. 0 or 1. Two same operations equal no operation.
2. The first 3 operations can be reduced to 1 or 0 operation. For example, flip all + flip even = flip odd. So the result of the first 3 operations is the same as either 1 operation or original.
3. The solution for n > 3 is the same as n = 3.
For example, 1 0 0 ….., I use 0 and 1 to represent off and on.
The state of 2nd digit indicates even flip; The state of 3rd digit indicates odd flip; And the state difference of 1st and 3rd digits indicates 3k+1 flip.

In summary, the question can be simplified as m <= 3, n <= 3. I am sure you can figure out the rest easily.

struct Solution {
    int flipLights(int n, int m) {
        if (m == 0 || n == 0) return 1;
        if (n == 1) return 2;
        if (n == 2) return m == 1? 3:4;
        if (m == 1) return 4;
        return m == 2? 7:8;
    }
};

23.17 LN 48. Majority Number III

http://www.lintcode.com/en/problem/majority-number-iii/

23.18 29. Divide Two Integers

Divide two integers without using multiplication, division and mod operator.

If it is overflow, return MAX_INT.

https://leetcode.com/problems/divide-two-integers/

我们知道,乘法是可以由加法来代替计算的,将除数一直累加直至超过被除数.但是仔细考虑之后发现,如果使用加法,那么时长可能会过长.假设给定1和10000000,由1加到10000000,最后的结果肯定是超时.

既然不能直接累加,那么还有什么新的方法呢?我们直到,二进制是可以表示所有数字的.那么在这题中使用二进制来逼近是较为迅速的办法.

假定商是l,那么l一定可以用二进制来表示,也即2的幂和,5=2²⁺²0.那么所需要做的也就是累加除数与2的幂次乘积,直至刚好超过被除数,然后从最大的次幂开始计算,如果当前的和加上该次幂大于被除数,那么放弃该次幂,如果加上该次幂仍然小于被除数,那么就加上该次幂.

举个例子,假设除数为3,被除数为16,那么商应该是5.我们从2的0次幂与除数的乘积也即2^{0x3=3开始,幂次逐渐增加,直至超过被除数.可以看出,当幂次达到2时刚好超过16（3x2}0+3x2^1+3x22=21>16).那么从3x2^{2开始往下累加,3x2}2=12>16,那么记录下2^{2=4.再看3x2}1,发现3x2^2+3x21=18>16,因此略过2^{1=2.再看3x2}0,发现发现3x2^2+3x20=15<16,那么将2^0=1记录下.次幂累加结束,计算一下商,分别记录了4和1,因此结果4+1=5,此答案也即为最终的商.

算法大概的思路差不多讲完了,还需要注意的就是边界问题,只有一个边界特例需要考虑Integer.MIN_VALUE和-1.此时的结果超过了Integer所能表示的最大范围,因此需要特殊处理.其次,为了简单起见,我们将除数和被除数的符号进行记录,然后将其转换为正数进行计算,这也涉及到溢出的问题,Integer.MIN_VALUE转换为正数之后会超过32位Integer所能表示的范围,因此在代码中使用long类型进行计算防止溢出.

此算法时间复杂度是O(logn).空间复杂度为O(logn)

https://kingsfish.github.io/2017/10/11/Leetcode-29-Divide-Two-Integers/

class Solution {
    public int divide(int dividend, int divisor) {
        if(dividend == -2147483648 && divisor == -1){//防止溢出 
            return 2147483647;
        }
        List<Long> list = new ArrayList<>();
        int end = dividend > 0 ? 1 : 0;
        int sor = divisor > 0 ? 1 : 0;
        long a = Math.abs((long)dividend);
        long b = Math.abs((long)divisor);
        int ret = 0;
        list.add(b);
        long i = 1;
        //记录除数与二次幂的乘积
        while (b <= a){
            b += b;
            i += i;
            list.add(b);
        }
        long sum = 0; //累加
        for (int j = list.size() - 2; j >= 0; j --){
            i >>= 1;
            if (sum + list.get(j) <= a){
                ret += i;
                sum += list.get(j);
            }
        }
        //根据除数以及被除数的正负确定返回值正负
        if (end + sor == 1){
            return -ret;
        } else {
            return ret;
        }
    }
}

23.19 204. Count Primes

Description:

Count the number of prime numbers less than a non-negative number, n.

https://leetcode.com/problems/count-primes/

class Solution {
public:
    int countPrimes(int n) {
        if(n<2) return 0;
        vector<bool> v(n, true);
        for(int i=2; i*i<n; ++i){ // why i*i?
            if(!v[i]) continue;
            int j=i+i;
            while(j<n)
                v[j]=false, j+=i;
        }
        return count(v.begin()+2, v.end(), true);
    }
};

After a little optimization:

class Solution {
public:
    int countPrimes(int n) {
        if(n<2) return 0;
        vector<bool> v(n, true);
        int c=0;
        for(int i=2;i<n;++i){
            if(!v[i]) continue;
            c++;
            if(i*i<n){
                int j=i+i;
                while(j<n)
                    v[j]=false, j+=i;
            }
        }
        return c;
    }
};

https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
https://www.geeksforgeeks.org/sieve-of-eratosthenes/
https://www.geeksforgeeks.org/sieve-eratosthenes-0n-time-complexity/ T:\(O(N)\)

Why i*i?

Everyone else is explaining why for a monolithic sieve (i.e. non-segmented). You need to check all prime factors up to the square root of the limit (e.g. N=49, we must check 7, but do not need to check anything higher, since any number divisible by a larger number would also be divisible by a number less than the square root of N, hence we would already have found it). I’m pretty sure this isn’t your question, which is instead about segmented sieves.

https://www.quora.com/Why-do-we-first-find-the-prime-numbers-up-to-square-root-of-N-in-segmented-sieve

23.20 504. Base 7

Given an integer, return its base 7 string representation.

Example 1:

Input: 100
Output: "202"

Example 2:

Input: -7
Output: "-10"

Note: The input will be in range of [-1e7, 1e7].

https://leetcode.com/problems/base-7/

class Solution {
public:
    string convertToBase7(int num) {
        if(num==0) return "0";
        if(num<0) return "-"+convertToBase7(-num);
        string s;
        while(num)
            s = to_string(num%7)+s, num/=7;
        return s;
    }
};

class Solution {
    public String convertToBase7(int num) {
        if(num==0) return "0";
        if(num<0) return "-"+convertToBase7(-num);
        String r="";
        while(num!=0){ r=Integer.toString(num%7)+r; num/=7;}
        return r;
    }
}

    public String convertToBase7(int num) {
        return Integer.toString(num,7);
    }

23.21 660. Remove 9

Start from integer 1, remove any integer that contains 9 such as 9, 19, 29…
So now, you will have a new integer sequence: 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, …
Given a positive integer n, you need to return the n-th integer after removing. Note that 1 will be the first integer.
Example 1: Input: 9, Output: 10

https://leetcode.com/problems/remove-9

struct Solution {
  int newInteger(int n) {
    long long res = 0, s = 1;
    while (n) {
      res += n % 9LL * s;
      n /= 9;
      s *= 10;
    }
    return res>INT_MAX?INT_MAX:res;
  }
};

After removing 9 from all numbers, we get a nonary number system. This question is to find the nonary presentation of a decimal number. 消除9就是说新的数字系统中不含9,这种数字系统叫nonary number system.

Java

public int newInteger(int n) {
    return Integer.parseInt(Integer.toString(n, 9));
}

Similar: http://bit.ly/2vv0JjM

This problem comes from a Google interview. You probably know that the number “4” is considered unlucky number in China. Here is the problem:

Number ‘4’ is considered an unlucky number in China because it is nearly homophonous to the word “death”. For this reason, there is a new number system similar to the decimal system but has no ‘4’. For example: 1,2,3,5,6,7…13,15…23,25…33,35…39,50…

Here 5 is 4 in decimal system, and 15 is 13… Write a function which takes as an input a positive number (Chinese number) and provides an output number (decimal number or error):

1 -> 1;
2 -> 2;
5 -> 4;
4 -> illegal;
15 -> 13;

The whole idea is based on that a Chinese number is a number in the nonary system and its digits are: 0, 1, 2, 3, 5, 6, 7, 8, 9. The ordinary nonary system has the digits: 0, 1, 2, 3, 4, 5, 6, 7, 8. Therefore we can convert the given Chinese number into an ordinary number in the nonary system. Then it is easy to get the decimal number having an ordinary nonary number.

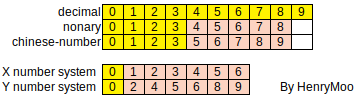
Conversion between number systems

Take 15 -> 13 as an example: 1. map from chinese to nonary 2. convert from nonary to decimal

string chinese2decimal(string s){
  if(s.find('4')!=string::npos) return "illegal";
  map<char,char> m={{'5','4'},{'6','5'},{'7','6'},{'8','7'},{'9','8'}};
  string r; // 1. map from chinese to nonary
  for(char c: s) r += m.count(c)?m[c]:c;
  int t=stoi(r), w=1, n=0, BASE=9; // 2. from nonary to decimal
  while(t) n += (t%10)*w, w*=BASE, t/=10;
  return to_string(n);
}

Can you think of the opposite function - decimalToChineseNumber?
Remove4需要Remove9作为一个中介. Take 13 -> 15 as an example. First, we convert 13 from decimal to nonary system and get 14 (1*9+4==13), then we map noary system’s 14 to chinese number system, where 1->1 and 4->5, so we get final result 15.
How about remove 7?
http://bit.ly/2wHvxwp
How about remove 1,3,7?
同样的方法,用7进制系统做中介,然后再map.见上图的X/Y number system.

其他给BASE Conversion有关的题目:

bit.html#repeated-dna-sequences
system-design.html#design-tinyurl
string.html#shortest-palindrome
facebook-2016-interview-questions-part-1.html#excel-sheet-column-title
bit.html#convert-a-number-to-hexadecimal

23.22 780. Reaching Points

A move consists of taking a point (x, y) and transforming it to either (x, x+y) or (x+y, y).

Given a starting point (sx, sy) and a target point (tx, ty), return True if and only if a sequence of moves exists to transform the point (sx, sy) to (tx, ty). Otherwise, return False.

Examples: Input: sx = 1, sy = 1, tx = 3, ty = 5 Output: True Explanation: One series of moves that transforms the starting point to the target is: (1, 1) -> (1, 2) (1, 2) -> (3, 2) (3, 2) -> (3, 5)

Input: sx = 1, sy = 1, tx = 2, ty = 2
Output: False

Input: sx = 1, sy = 1, tx = 1, ty = 1
Output: True

https://leetcode.com/problems/reaching-points/

class Solution {
public:
    /*bool reachingPoints(int sx, int sy, int tx, int ty) {
        return rec(sx,sy,tx,ty);
    }
    bool rec(long long sx, long long sy, long long tx, long long ty){
        if(sx==tx and sy==ty) return true;
        if(tx<sx or sy>ty) return false;
        return rec(sx,sx+sy,tx,ty) or rec(sx+sy,sy,tx,ty);
    }*/
    bool reachingPoints(int sx, int sy, int tx, int ty) {
        if(tx<sx||ty<sy) return 0;
        if(sx==tx) return (ty-sy)%sx==0;
        if(sy==ty) return (tx-sx)%sy==0;
        if(tx==ty) return 0;
        if(tx>ty) return reachingPoints(sx,sy,tx%ty,ty);
        else return reachingPoints(sx,sy,tx,ty%tx);
    }
};

23.23 878. Nth Magical Number

A positive integer is magical if it is divisible by either A or B.

Return the N-th magical number. Since the answer may be very large, return it modulo 10^9 + 7.

Example 1:

Input: N = 1, A = 2, B = 3
Output: 2
Example 2:

Input: N = 4, A = 2, B = 3
Output: 6
Example 3:

Input: N = 5, A = 2, B = 4
Output: 10
Example 4:

Input: N = 3, A = 6, B = 4
Output: 8

https://leetcode.com/problems/nth-magical-number/

Least common multiple: lcm(a, b) = (a*b)/gcd(a,b) (证明可以根据数论里的“每个数都可以表示成素因子的乘积”)

gcd(a,b)可用欧几里得算法求解,但在用上面公式计算lcm(a,b)的时候,a*b有可能会溢出,所以要定义合适的类型,以免溢出.

Linear: \(O(N)\)

class Solution {
public:
    int nthMagicalNumber(int N, int A, int B) {
        if(A==B) return (N*1LL*A)%1000000007LL;
        long long r=0LL, c=0LL, tmp=r;
        for(long long i=1LL, j=1LL; i<=N and j<=N;){
            if(i*A < j*B) tmp=i*A, i++;
            else tmp=j*B, j++;
            if(tmp>r) r=tmp, c++;
            if(c==N) return r%1000000007LL;
        }
    }
};

Logrithm: \(O(LogN)\), binary search + LCM

class Solution {
public:
    int nthMagicalNumber(int N, int A, int B) {
        long l=0, h=LONG_MAX, m=0;
        int lcm=A*B/gcd(A,B);
        while(h>l+1){
            m=l+(h-l)/2;
            long n=m/A+m/B-m/lcm;
            if(n>=N) h=m; else l=m;
        }
        return int(h%1000000007);
    }
    int gcd(int x,int y){
        if(y==0) return x;
        else return gcd(y, x%y);
    }
};

Refer to: https://www.geeksforgeeks.org/find-nth-magic-number/