Chapter 37 Google 2016 10

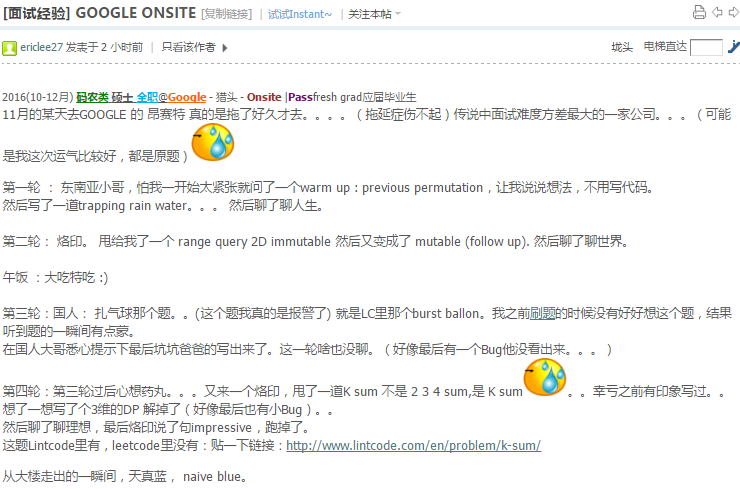
37.1 previous permutation

http://www.lintcode.com/en/problem/previous-permutation/

http://lhearen.top/2016/10/19/Previous-Permutation/

void previousPermutation(vector<int>& arr){
    int i = arr.size()-2, j = i+1;
    while(i>0 && arr[i] <= arr[i+1]) i--; 
    while(j>0 && arr[j] >= arr[i]) j--; 
    if(j == 0) return ;
    swap(arr[i++], arr[j]);
    j = arr.size()-1;
    while(i < j) swap(arr[i++], arr[j--]); //reverse;
}

注意第二个例子,后缀上升序列其实就是一个数,0,所以pivot是前面的3!

37.2 next permutation

https://leetcode.com/problems/next-permutation/

https://www.nayuki.io/page/next-lexicographical-permutation-algorithm

struct Solution {
    void nextPermutation(vector<int>& nums) {
        int L = nums.size(), i = L-1;
        while (i-1>=0 && nums[i-1] >= nums[i]) i--;
        if (i==0)
            reverse(nums.begin(), nums.end());
        else{
            int l = i-1, r=L-1;
            for(int j=L-1; j>=0; j--){
                if(nums[j] > nums[l]){
                    r=j;
                    break;
                }
            }
            swap(nums[l], nums[r]);
            r = L-1;
            ++l;
            while(l < r) swap(nums[l++], nums[r--]);
        }
    }
};

37.3 Trapping Rain Water I/II

https://leetcode.com/problems/trapping-rain-water/

http://www.cnblogs.com/grandyang/p/4402392.html

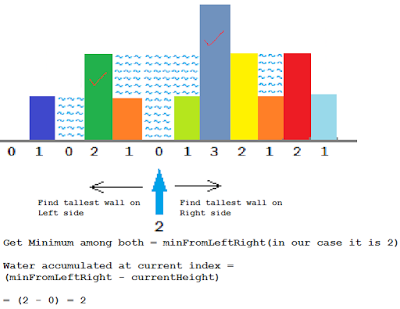
我把这道题的解法叫做两大夹一小maxMinMax,因为每点的水的高度可由下面的式子求出来:

\(Water[i] = max(0, min(maxleft[i], maxright[i]) - height[i])\)

T: \(O(N)\), S: \(O(N)\), 3 sweep

struct Solution {// maxMinMax, 9ms
    int trap(vector<int>& height) {
        int L = height.size(), r = 0;
        if (L <= 2) return r;
        vector<int> lm(L), rm(L); // left max, right max
        for (int i = 0, t=0 ; i<L; ++i) lm[i] = t = max(t, height[i]);// chain-assignment
        for (int i = L - 1, t=0 ; i >= 0; --i) rm[i] = t = max(t, height[i]);
        for (int i = 1; i<L - 1; ++i) // ignore the first and last point safely
            r += max(min(lm[i - 1], rm[i + 1]) - height[i], 0);
        return r;
    }
};

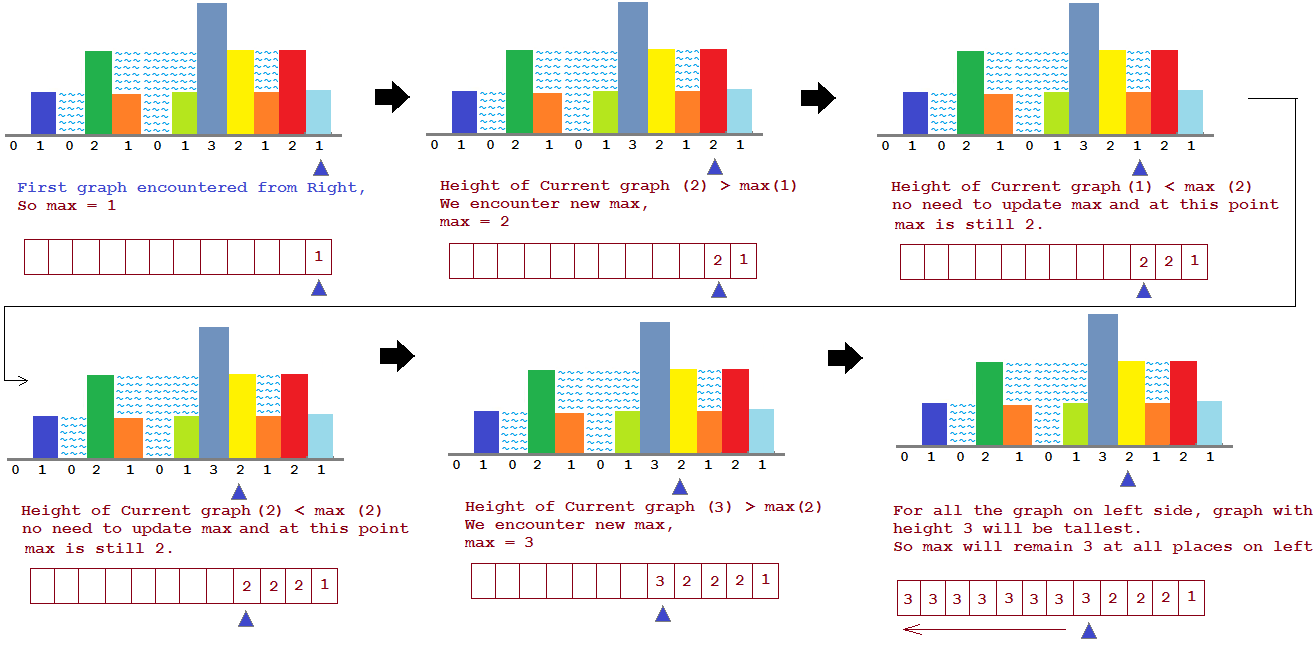
在算leftmax和rightmax的时候,是否比较的时候要和自己比?其实都不影响结果.下面的方法是不和自己比较也得出相同的结果.

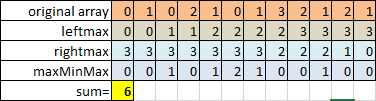
不过不和自己比较的时候,要初始化leftmax[0]和rightmax[L-1]为0,然后开始循环. 所以为了编码的简洁,干脆在比较的时候包括自己.

T: \(O(N)\), S: \(O(1)\), One sweep

struct Solution {// maxMinMax, 9ms
    int trap(vector<int>& A) {
        int L = A.size(), left=0, right=L-1, res=0, maxleft=0, maxright=0;
        while(left<=right){
            if(A[left]<=A[right]){
                if(A[left]>=maxleft) maxleft=A[left];
                else res+=maxleft-A[left];
                left++;
            } else {
                if(A[right]>=maxright) maxright= A[right];
                else res+=maxright-A[right];
                right--;
            }
        }
        return res;
    }
};

37.4 407. Trapping Rain Water II

https://leetcode.com/problems/trapping-rain-water-ii/

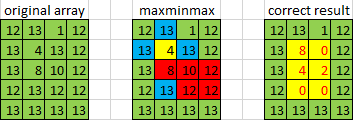
作为上题在3D空间的扩展,自然的想“故技重施”,结果发现行不通.以M[1][1]点4为例,左右前后的最大值都是13,结果看起来是9,其实是错的.因为水其实可以从红色的那片区域溜走.试图对maxminmax算法改进也失败.

DFS/BFS + Heap

因为水可以从边上的缺口流走,就以这种边缘的缺口为起始点,用DFS搜索比缺口还低的点.如果遇到比起始点还高的点,那么它一定是更高层的边缘点,所以将其加入一个priority queue,下一次搜索的时候好用.

整个思路好似攻打一堆城堡,总是从挖墙脚开始,由外而内,由低到高.

这题有几个关键点:

1. 矩阵最外层的点必然不是含水的点,它必定是边缘点!!! 所以可以用类似sprial matrix traversal的方法来初始化这个priority queue.

2. 初看这题是DFS,其实只要保留上一次取出来的高度的最大值,BFS就可以解决.因为当从priority queue(Q)取出黄点12的时候,必定是Q中高度最小的点.在和四周的点比较的时候,如果遇到高度更小的点(10),累加入总结果(r+=12-10),同时也把新点加入Q.这个加入的新点(10)一定会从Q中第一个被取出,但之前的高度(12)必须要保留下来以便累加入总结果的时候用.

通常的BFS采用FIFO Queue,和DFS行走的路径是不同的,但这里因为用的是Priority Queue,BFS行走的路径和DFS的相同!!!

http://www.cnblogs.com/grandyang/p/5928987.html

相关算法:

Dijkstra https://www.youtube.com/watch?v=8Ls1RqHCOPw

Flood Fill https://en.wikipedia.org/wiki/Flood_fill

Check this animation

BFS + Heap:

struct Solution {
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.empty()) return 0;
        int m = heightMap.size(), n = heightMap[0].size(), res = 0, mx = INT_MIN;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        vector<vector<int>> dir{{0,-1},{-1,0},{0,1},{1,0}};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    q.push({heightMap[i][j], i * n + j});
                    visited[i][j] = true;
                }
            }
        }
        while (!q.empty()) {
            auto t = q.top(); q.pop();
            int h = t.first, r = t.second / n, c = t.second % n;
            mx = max(mx, h);
            for (int i = 0; i < dir.size(); ++i) {
                int x = r + dir[i][0], y = c + dir[i][1];
                if (x < 0 || x >= m || y < 0 || y >= n || visited[x][y]) continue;
                visited[x][y] = true;
                if (heightMap[x][y] < mx) res += mx - heightMap[x][y];
                q.push({heightMap[x][y], x * n + y});
            }
        }
        return res;
    }
};

DFS + Heap:

struct customLess { bool operator()(int *a, int *b) { return a[2] > b[2]; } };
struct Solution { // 37 lines, 49 ms, 96%
    priority_queue <int*, vector<int*>, customLess> pq;
    int dfs(vector<vector<int>> &hm, vector<vector<bool>> &visited, int i, int j, int h, int st) {
        int r = hm.size(), c = hm[0].size();
        if (i >= r || i<0 || j>c - 1 || j<0 || (visited[i][j] && st != 0)) return 0;
        visited[i][j] = true;
        if (hm[i][j]>h) {
            pq.push(new int[3]{ i,j,hm[i][j] });
            return 0;
        }
        return dfs(hm, visited, i + 1, j, h, 1) + dfs(hm, visited, i, j + 1, h, 1) +
            dfs(hm, visited, i - 1, j, h, 1) + dfs(hm, visited, i, j - 1, h, 1) + (h-hm[i][j]);
    }
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.size()<3 || heightMap[0].size()<3) return 0;
        vector<int> tmpv(heightMap[0].size(), 0);
        vector<vector<bool>> visited(heightMap.size(), vector<bool>(heightMap[0].size(), false));
        int r = heightMap.size(), c = heightMap[0].size(), i, j, k, rst = 0;
        int *tmp, *tmp2;
        for (i = 0; i<r; i++) {
            pq.push(new int[3]{ i,0,heightMap[i][0] });
            pq.push(new int[3]{ i,c - 1,heightMap[i][c - 1] });
        }
        for (j = 1; j<c - 1; j++) {
            pq.push(new int[3]{ 0,j,heightMap[0][j] });
            pq.push(new int[3]{ r - 1,j,heightMap[r - 1][j] });
        }
        while (!pq.empty()) {
            tmp2 = pq.top(), pq.pop();
            rst += dfs(heightMap, visited, tmp2[0], tmp2[1], tmp2[2], 0);
            delete[] tmp2;
        }
        return rst;
    }
};

Python DFS + Heap:

from heapq import *
class Solution(object):
    def trapRainWater(self, heightMap):
        """
        :type heightMap: List[List[int]]
        :rtype: int
        """
        if len(heightMap) < 3 or len(heightMap[0]) < 3: return 0
        m, n, bd = len(heightMap), len(heightMap[0]), []
        for x, y in zip([0]*n+[m-1]*n+range(1,m-1)*2, range(n)*2+[0]*(m-2)+[n-1]*(m-2)):
        heappush(bd, [heightMap[x][y], x, y])
        heightMap[x][y] = 0
        res = 0
        while bd:
            h, x, y = heappop(bd)
            res = self.dfs(h, x, y, bd, heightMap, m, n, res)
        return res

    def dfs(self, h, x, y, bd, heightMap, m, n, res):
        for dx, dy in zip([-1,1,0,0], [0,0,-1,1]):
            if x+dx > 0 and x+dx < m - 1 and y+dy > 0 and y+dy < n - 1 and heightMap[x+dx][y+dy]:
                tmpH = heightMap[x+dx][y+dy]
                heightMap[x+dx][y+dy] = 0
                if tmpH <= h:
                    res += h - tmpH
                    res = self.dfs(h, x+dx, y+dy, bd, heightMap, m, n, res)
                else: heappush(bd, [tmpH, x+dx, y+dy])
        return res

Another fast C++ solution using std::map (99~100%, 40+ ms):

https://discuss.leetcode.com/topic/62817/share-my-fast-c-solution-using-std-map-99-100-40-ms

This is not a new algorithm, just a performance-aware implementation.

I have tried 2 versions, binary min heap and simply std::map; surprisingly using std::map brings more performance gain rather than binary heap (60+ ms).

I added my comment in the codes, and here I am pointing out some effort I have done.

Instead of using another new matrix to record the node traversal, I abuse the original input height map. There are quite a few times that the newly inserted node has the same height of the current one; in this case my implementation make new insertion in constant time. (Minor) I found the corner of the height map is irrelevant, so I don’t put them into the std::map initially.

小优化:

1. 为了不重复检查,BFS需要用一个bitmap来记录矩阵的某一点是否被访问过.因为原始矩阵(heights)所有值为正,可以用heights[i][j]=-1来表示该点已经被访问过了.

2. The corner of the height map is irrelevant.

struct Solution {
    int trapRainWater(vector<vector<int>>& heightMap) {
        int w = heightMap.size();
        //check the dimension...otherwise gotta do boundary checking in the next step anyway
        if(w<=2)return 0;
        int h = heightMap[0].size();
        if(h <=2)return 0;
        map<int,vector<pair<int,int>>> m;
        //initiate the map : push the posisions on the 4 edges except corners
        //abuse the input :P
        //setting heightMap[x][y] to 0 means the node is in the map or traversed
        for(int i=1;i+1<w;++i) {
            m[heightMap[i][0]].push_back({i,0});
            m[heightMap[i][h-1]].push_back({i,h-1});
            heightMap[i][0] = heightMap[i][h-1] = -1;
        }
        for(int i=1;i+1<h;++i) {
            m[heightMap[0][i]].push_back({0,i});
            m[heightMap[w-1][i]].push_back({w-1,i});
            heightMap[0][i] = heightMap[w-1][i] = -1;
        }
        //not wanna process the 4 corners, for they are irrelevant to the problem, right?
        heightMap[0][0] = heightMap[0].back() = heightMap.back()[0] = heightMap.back().back() = -1;
        int ret = 0;
#define X first
#define Y second
        while(!m.empty()) {
            auto b = m.begin();
            int height = b->first;
            auto& v = b->second;
            for(int i = 0;i<v.size();++i) {
                auto p = v[i];
                pair<int,int> nodes[4] = {p,p,p,p};
                --nodes[0].X;
                ++nodes[1].X;
                --nodes[2].Y;
                ++nodes[3].Y;
                for(int i=0;i<4;++i) {
                    p = nodes[i];
                    if(p.X<0||p.Y<0||p.X>=w||p.Y>=h || heightMap[p.X][p.Y]==-1) continue;
                    ret += max(0,height-heightMap[p.X][p.Y]);
                    heightMap[p.X][p.Y] = max(heightMap[p.X][p.Y],height);
                    //push to map
                    //if the new height is the same, we can save some time on BST insertion
                    if(heightMap[p.X][p.Y] == height)v.push_back(p);
                    else m[heightMap[p.X][p.Y]].push_back(p);
                    heightMap[p.X][p.Y] = -1; // mark it as traverse
                }
            }
            m.erase(b);
        }
        return ret;
    }
};

T: ?; O: ?

https://code.google.com/codejam/contest/11274486/dashboard#s=p1

37.5 KSum

几个关键点: 排序, Two pointers, Hashtable, 去重, 复杂度

复杂度讨论: https://discuss.leetcode.com/topic/660/any-solution-which-is-better-than-o-n-2-exists

K-SUM Time complexisty lower bound: \(\Omega(N^{\lceil{k/2}\rceil})\)

So, O(2sum) = O(N), O(3sum) = O(N^2), O(4sum) = O(N^2), O(5sum) = O(N^3)

2SUM的hashtable方法在k(k=2)是偶数的时候可以提高效率,如果k是奇数就不行,可以理解为什么上面的式子使用了\(\lceil{k/2}\rceil\).

37.6 2sum

如果已经排序,O(N)的方法有两个,two pointer和hastable. two pointer效率更高,也免去了对额外数据结构hashtable的需要.

如果没排序,只有hashtable可以达到O(N).

https://leetcode.com/problems/two-sum/

func twoSum(nums []int, target int) []int {
    lookup := make(map[int]int)
    for i, num := range nums {
        if j, ok := lookup[target-num]; ok {
            return []int{j, i}
        }
        lookup[nums[i]] = i
    }
    return nil
}

https://leetcode.com/problems/two-sum-ii-input-array-is-sorted/

https://leetcode.com/problems/two-sum-iii-data-structure-design/

sorted 2sum 去重:

void twoSum(VVI &allSol, VI& sol,VI& num, int start, int end, int target ) {
    while(start<end) {
        int sum = num[start]+num[end];
        if(sum==target) {
            sol.push_back(num[start]), sol.push_back(num[end]);
            allSol.push_back(sol);
            sol.pop_back(), sol.pop_back();
            start++, end--;
            while(num[start]==num[start-1]) start++; //!!remove duplicates
            while(num[end]==num[end+1]) end--; //!!remove duplicates
        } else if(sum<target)
            start++;
        else
            end--;
    }
}

37.7 3sum

https://leetcode.com/problems/3sum/ (去重)

去重其实2sum也可能发生,不过恰好3sum这道题要求而2sum没有要求.去重有两个办法,1是在移动指针的时候去重,2是把结果加入set利用set的属性去重.当然前者效率更高.

Tricky part is to remove duplicates.

Method 1: use set and _2sum()

struct Solution { //TLE
    vector<vector<int>> threeSum2(vector<int>& nums) {
        set<vector<int>> svi;
        for (int i=0;i<nums.size();++i){//O(N)
            auto tmp = _2sum(nums, i+1, -nums[i]); // return all pairs!!!
            if (!tmp.empty()){
                for(auto pr: tmp){
                    vector<int> vi = {nums[i], pr.first, pr.second};
                    sort(vi.begin(), vi.end());//KlogK K=3
                    svi.insert(vi);
                }
            }
        }
        vector<vector<int>> r;
        for(auto x: svi){r.push_back(x);}
        return r;
    }
    vector<pair<int,int>> _2sum(vector<int>& nums, int head, int target){//O(N), return all!!!
        vector<pair<int,int>> r;
        unordered_set<int> si;
        for(int i=head; i<nums.size();++i)
            (si.count(target-nums[i]))?  r.push_back({target-nums[i], nums[i]}) : si.insert(nums[i]);
        return r;
    }
};

Method 2: sort and move two pointers

这里讲一点,先整体排一次序,然后枚举第二个数字的时候不需要重复看前面的. 比如排好序以后的数字是a b c d e f,那么第一次枚举a,在剩下的b c d e f中进行2 sum,完了以后第二次枚举b,只需要在c d e f中进行2sum好了,而不是在a c d e f中进行2sum!!

struct Solution {
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> r;
        if (nums.size()<3) return r;
        sort(nums.begin(), nums.end());// O(NLogN)
        for(int i=0;i<nums.size()-2;++i){ //O(N^2)
            if (i>=1 and nums[i]==nums[i-1]) continue; //!!remove duplicates i
            int j=i+1, k=nums.size()-1;
            while(j<k){
                if ( nums[j]+nums[k]+nums[i] == 0 ){
                    r.push_back({nums[i],nums[j],nums[k]});
                    while (++j<k && nums[j]==nums[j-1]); //!!remove duplicates j
                    while (j<--k && nums[k]==nums[k+1]); //!!remove duplicates k
                }else if(nums[j]+nums[k]+nums[i] < 0){
                    ++j;
                }else --k;
            }
        }
        return r;
    }
};

参考资料和论文:

http://cs.smith.edu/~orourke/TOPP/P11.html

https://en.wikipedia.org/wiki/3SUM

Paper1, Paper2

37.8 3Sum Closest

https://leetcode.com/problems/3sum-closest/

由于不是精确的等于关系,这道题只能用two pointer的方法!!!hashtable doesn’t work in this case!

struct Solution {
    int threeSumClosest(vector<int>& nums, int target) {
        int d = INT_MAX, r;
        sort(nums.begin(), nums.end());
        for (int i=0;i<nums.size()-2;++i){
            int j = i+1, k=nums.size()-1;
            while(j<k){
                int tmp=nums[i]+nums[j]+nums[k];
                if (d>abs(tmp-target))
                    d = abs(tmp-target), r=tmp;
                if (d==0)
                    return target;
                else if(tmp>target)
                    --k;
                else ++j;
            }
        }
        return r;
    }
};

37.9 259. 3Sum Smaller

https://leetcode.com/problems/3sum-smaller/

37.10 18. 4Sum

https://leetcode.com/problems/4sum/

4sum的hash算法:

\(O(N^2)\)把所有pair存入hash表,并且每个hash值下面可以跟一个list做成map, map[hashvalue] = list,每个list中的元素就是一个pair, 这个pair的和就是这个hash值,那么接下来求4sum就变成了在所有的pair value中求 2sum,这个就成了线性算法了,注意这里的线性又是针对pair数量(\(N^2\))的线性,所以整体上这个算法是\(O(N^2)\),而且因为我们挂了list, 所以只要符合4sum的我们都可以找到对应的是哪四个数字.

https://discuss.leetcode.com/topic/47834/share-my-k-sum-c-solution

struct Solution {
    vector<vector<int>> fourSum(vector<int>& nums, int target, int k_=4) {
        k = k_;
        sort(nums.begin(), nums.end());
        tmp = vector<int>(k, 0);
        dfs(nums, target, k, 0);
        return res;
    }
private:
    vector<vector<int>> res;
    vector<int> tmp;
    int k;
    void dfs(vector<int> &nums, int target, int n, int start) {
        if (n == 2) {
            int end = nums.size() - 1;
            while (start<end) {
                if (nums[start] + nums[end] == target) {
                    tmp[k - 2] = nums[start], tmp[k - 1] = nums[end];
                    res.push_back(tmp);
                    while (++start<end&&nums[start - 1] == nums[start]);// remove duplicates
                    while (--end>start&&nums[end + 1] == nums[end]);// remove duplicates
                } else if (nums[start] + nums[end]>target)
                    end--;
                else
                    start++;
            }
        } else {
            int len = nums.size() - n;
            while (start <= len) {
                tmp[k - n] = nums[start];
                dfs(nums, target - nums[start], n - 1, start + 1);
                while (++start <= len&&nums[start - 1] == nums[start]);
            }
        }
    }
};

37.11 454. 4Sum II

https://leetcode.com/problems/4sum-ii/

http://www.bo-song.com/leetcode-4sum/

http://www.cnblogs.com/grandyang/p/6073317.html

这道题是之前那道4Sum的延伸. 但是这题只能用hashtable,不能用two pointer的方法.

那么brute force的方法就是遍历所有的情况,时间复杂度为\(O(n^4)\).但是我们想想既然Two Sum那道都能将时间复杂度缩小一倍,那么这道题我们使用哈希表是否也能将时间复杂度降到\(O(n^2)\)呢?答案是肯定的,我们如果把A和B的两两之和都求出来,在哈希表中建立两数之和跟其出现次数之间的映射,那么我们再遍历C和D中任意两个数之和,我们只要看哈希表存不存在这两数之和的相反数就行了.

理解的困难点在如果AB的pair和CD的pair配对之后,是否有必要在做AC和BD的pair的配对?答案是没有必要!

int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D){ //O(N^2)
    int ret = 0;
    unordered_map<int, int> m;
    for(auto a : A) for(auto b : B) m[a + b]++;
    for(auto c : C) for(auto d : D) ret += m[-(c + d)];
    return ret;
}

or use two hashtables:

int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {
    int res = 0, n = A.size();
    unordered_map<int, int> m1, m2;
    for (int i = 0; i < n; ++i) for (int j = 0; j < n; ++j) ++m1[A[i] + B[j]], ++m2[C[i] + D[j]];
    for (auto a : m1) res += a.second * m2[-a.first];
    return res;
}

37.12 ksum I

http://www.lintcode.com/en/problem/k-sum/

Given n distinct positive integers, integer k (k <= n) and a number target. Find k numbers where sum is target. Calculate how many solutions there are?

Distinct input, so no duplicates.

只要求返回个数,而且规定了所有数是正数!!!

所以不需要降维的那种方法,用动态规划,无论K为多少,复杂度都是O(N^3).

这道题和Distinct Subsequence很像.

DP 3D:

https://segmentfault.com/a/1190000004984393

DP 2D: http://www.cnblogs.com/yuzhangcmu/p/4279676.html

struct Solution {
    int ans[105][1005];
    int kSum(vector<int> A, int K, int target) {
        ans[0][0] = 1;
        for(int i = 0; i < A.size(); ++i)
            for(int j = K; j > 0; j--)
                for(int k = target; k >= A[i]; k--) {
                    ans[j][k] += ans[j - 1][k - A[i]];
                    if(ans[j][k] > 2147483647)
                        return -1;
                }
        return ans[K][target];
    }
};

37.13 ksum II

http://www.lintcode.com/en/problem/k-sum-ii/

Given n unique integers, number k (1<=k<=n) and target. Find all possible k integers where their sum is target.

这道题才是接近真正的ksum-hard问题!因为不需要去重,所以难度稍微小了一点点,但是问题的复杂度不变.

如果用Two pinter的方法. T: \(O(n^{k-1})\); 如果用hashtable空间换时间的方法,可以逼近极限.

http://westpavilion.blogspot.com/2014/02/k-sum-problem.html

k sum problem (k 个数的求和问题)

问题陈述:

在一个数组,从中找出k个数(每个数不能重复取.数组中同一个值有多个,可以取多个),使得和为零.找出所有这样的组合,要求没有重复项(只要值不同即可,不要求在原数组中的index不同)

解法:

2 sum 用hash table做,可以时间\(O(n)\),空间\(O(n)\).

2 sum 如果用sort以后,在前后扫描,可以时间\(O(nlogn + n) = O(nlogn)\),空间\(O(1)\).

2 sum 用hash table做的好处是快,但是等于是利用了不用排序的特点.排序的办法,在高维度(也就是k sum问题,k>2)的时候,nlogn就不是主要的时间消耗成分,也就更适合2sum的sort后双指针扫描查找的办法.

那么,对于k sum, k>2的,如果用sort的话, 可以 对 n-2的数做嵌套循环,因为已经sort过了,最后剩下的两维用2 sum的第二个办法, 时间是\(O(nlogn + n^{k-2} * n) = O(n^{k-1})\),空间\(O(1)\). 但是这样跟纯嵌套循环没有什么区别,只是最后一层少了一个因子n.有什么办法能优化?

就是说,对于 k sum (k>2) 问题 (一个size为n的array, 查找k个数的一个tuple,满足总和sum为0), 有没有时间复杂度在\(O(n^{k-2})\)的办法?

之前常规的一层一层剥离,n的次数是递增的.只有在最后一层,还有两个维度的时候,时间开销上减少一个n的因子,但是这样时间开销还是太多.

我们可以通过对问题分解(Divide and Conquer)来解决.

举个例子 ...-5,-4,-3,-2,-1, 0,1, 2, 3, 4, 5....要找 4 sum = 0

那么先分解

4 分成 2 sum + 2 sum 来解决,但是这里的子问题2 sum没有sum=0的要求,是保留任何中间值.只有当子问题的2 sum解决以后,回归原问题的时候,我们才又回归原始的2 sum问题,这时候sum=0.

子问题,空间和时间消耗,都是\(O(n^2)\), 回归大问题,时间消耗,是\(O(n^2)\).

假设k sum中\(k = 2^m\), 那么一共有m层,会有m次分解.

分解到最底层,时间空间消耗 从原始\(O(n)\)变为新的\(O(n^2)\).

分解到次底层,时间空间消耗 从\(O(n^2)\)变为新的\(O((n^2)^2)\).

…

到达最顶层,时间空间消耗就都变成了\(O(n^{2m}) = O(n^{2LogK})\).

和之前的方法\(O(n^{k-1})\)相比,\(O(n^{2Logk})\)的时间是少了很多,但是空间消耗却很大.

因为子问题无法确定把哪一个中间结果留下,那么就需要把子问题的结果全部返回,到最后,空间消耗就很大了.整体效果算是空间换时间吧.

通过问题的分解 + hashtable的运用,能明显减少时间消耗, 但是空间消耗变大是个问题.

比如说,如果有\(10^6\)的int类型数组,我如果用这个hashtable的办法,就要有\(10^{12}\)的pair,这就有10T以上的空间消耗.

问题的分解是个很好的思路,但是中间值得保留迫使空间消耗增大,这和用不用hashtable倒没有很大关系,只是说,如果不用hashtable,时间消耗会更大.

另外,还有一些题目的变形,比如如果要求所有组合,满足sum < C, sum = C, sum > C, 或者是 closest to C.(C是常数).

遇到这些变形的时候,hashtable的做法就显得乏力了,但是嵌套循环的方式却仍是可行的.尤其是对closest to k这种非确定性的要求.

http://maider.blog.sohu.com/276593093.html

Problem:

Given an unsorted array, determine if there are K elements that sum up to SUM.

My solution: I use the hashtable and recurrence to solve this problem. No matter what K is, I will call the function recursively until the problem is divided into numerous 2sum problems. The time complexity of my solution is O(n^(k-1)), which is not optimal as far as we know.

Sample code:

public class KSum {
   public static void main(String... args) {
       int seed[] = new int[] { 100, 1, 2, 3, 4, 5, 6, 7, 8, 11, 9, 14, 10, 12, -8 };
       System.out.println(kSumHashTable(seed, 4, 15));
   }

   public static boolean kSumHashTable(int[] seed, int k, int sum) {
       Hashtable ht = establishHashTable(seed);
       return findInHashtable(seed, ht, k, 0, sum);
   }

   private static Hashtable establishHashTable(int[] seed) {
       Hashtable ht = new Hashtable();
       for (int i = 0; i < seed.length; i++) {
           ht.put(seed[i], seed[i]);
       }
       return ht;
   }

   private static boolean findInHashtable(int[] seed, Hashtable ht, int k,
           int index, int sum) {
       if (k == 1) {
           if (ht.contains(sum)) {
               System.out.print(sum);
               return true;
           }
       } else {
           for (int j = index; j < seed.length; j++) {
               ht.remove(seed[j]);
               if (findInHashtable(seed, ht, k - 1, j + 1, sum - seed[j])){
                   System.out.print("," + seed[j]);
                   ht.put(seed[j], seed[j]);
                   return true;
               }
               ht.put(seed[j], seed[j]);
           }
       }
       return false;
   }
}

Updated : 11/26/2013 Actually, the subset sum problem is an NP-complete problem. I am not good at NP problem even after reading chapter 34 in Introduction to Algorithm. So here I just leave a link on Wikipedia for anyone would like to dig into it:http://en.wikipedia.org/wiki/Subset_sum_problem

---

---

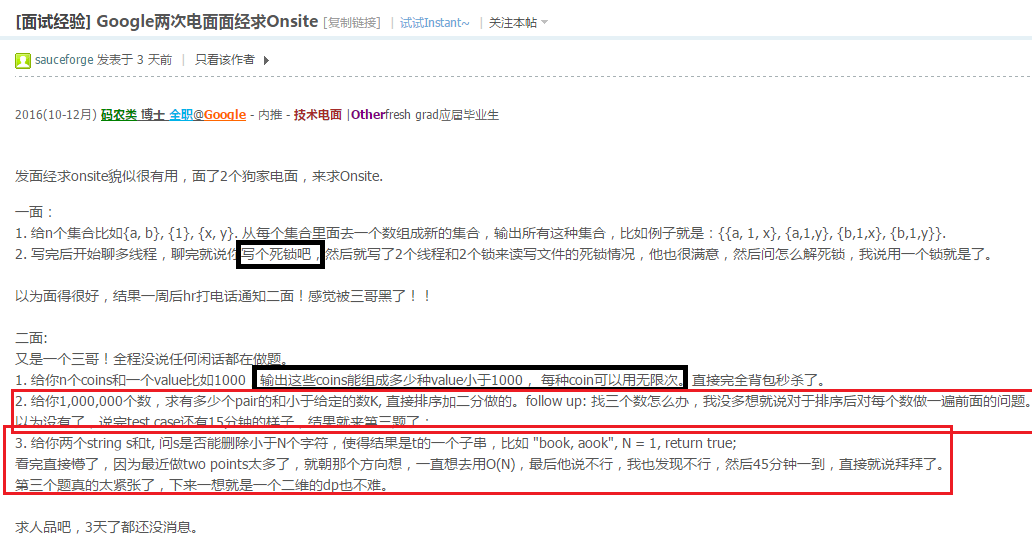
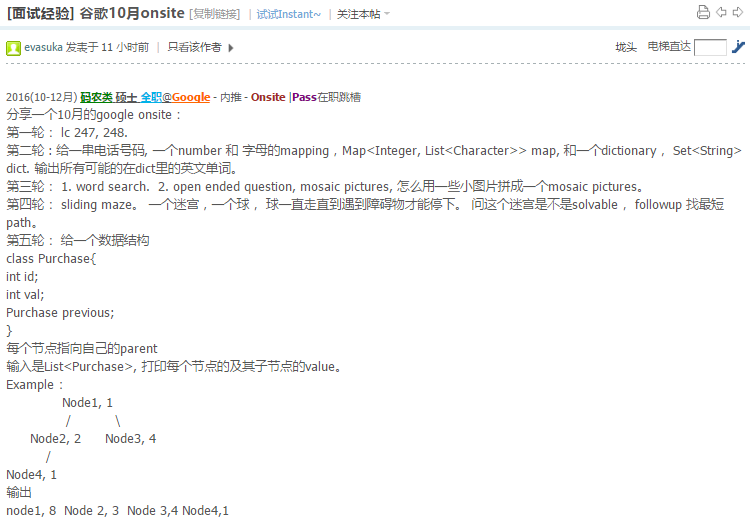
对的,只把碰到障碍物的点放入队列,其实是找最少操作次数的路径.最短路径不太准确.

若是寻找最少拐弯次数的sliding路径,我写了一下BFS的,只把碰到墙之前的Cell入队,看是不是这个意思:

// a: 2D maze (0 = pass, 1 = wall)
// s, e: start and end cells of maze
int minTurns(const vector<vector<int>>& a, Cell& s, Cell& e) {
  queue<pair<Cell, int>> q; // pair(cell, direction)
  map<Cell, int> turns; // accumulative number of turns at cell 
  turns[s] = 0; // start from s
  for (int d = 0; d < 4; ++d) q.emplace(s, d); // search all directions from s
  while (!q.empty()) {
    Cell c(q.front().first); int d = q.front().second, numTurns = turns[c]; q.pop();
    while (c != e && accessible(a, c, d)) continue; // search in direction dirs[d]
    if (c == e) return numTurns; // goal is found
    if (turns.count(c)) continue; // skip if visited-google 1point3acres
    q.emplace(c, d+1); q.emplace(c, d+3); // turn 90 and -90 degrees to search
    turns[c] = numTurns + 1;
  }
  return -1; // cannot reach goal of maze
}

方向dirs和helper function “accessible”定义如下:

typedef pair<int, int> Cell;
vector<Cell> dirs = {{1,0},{0,1},{-1,0},{0,-1}};
// Check if we can move at cell c in direction dirs[d].
// Overwrite c by moving one unit if accessible. 
bool accessible(const vector<vector<int>>& a, Cell& c, int d) {
  int i = c.first + dirs[d%4].first, j = c.second + dirs[d%4].second;
  if (i < 0 || i >= a.size() || j < 0 || j >= a.size() || a[i][j]) return false;  
  c.first = i; c.second = j; return true;      
}

http://www.1point3acres.com/bbs/thread-211354-1-1.html