Chapter 12 Stack and Queue
栈和PQ是站着的, Queue和Deque是躺着的.
难题主要在递增栈,递增Q的使用.
12.1 Remove duplicates from string and keep lexicographical order
Given a string which contains only lowercase letters, remove duplicate letters so that every letter appear once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.
Example:
Given "bcabc"
Return "abc"
Given "cbacdcbc"
Return "acdb" https://leetcode.com/problems/remove-duplicate-letters/
http://bookshadow.com/weblog/2015/12/09/leetcode-remove-duplicate-letters/
https://www.hrwhisper.me/leetcode-remove-duplicate-letters/
http://www.1point3acres.com/bbs/thread-182619-1-1.html
12.1.1 Recursion
class Solution(object):
def removeDuplicateLetters(self, s):
for c in sorted(set(s)):
suffix = s[s.index(c):]
if set(suffix) == set(s):
return c + self.removeDuplicateLetters(suffix.replace(c, ''))
return ''class Solution {
public:
string removeDuplicateLetters(string s) {//O(NK)
auto getset = [](string s) {
set<char> sc;
for_each(s.begin(), s.end(), [&sc](char c) { sc.insert(c); });
return sc;
};
set<char> sc = getset(s);//O(N)
for (char c : sc) { //STL set are ordered O(K)
int i = s.find(c);//O(N)
string suffix = s.substr(i);
if (getset(suffix).size() == sc.size()) {
if (suffix.size()==sc.size()) return suffix;
suffix.erase(remove(suffix.begin(),suffix.end(),c), suffix.end());//O(N)
return c+removeDuplicateLetters(suffix);
}
}
return "";
}
};12.1.2 Stack + Counter
使用栈(Stack)数据结构对上述算法进行优化,可以使时间复杂度缩减为\(O(N)\)
算法步骤:
首先计算字符串s中每一个字符出现的次数,得到字典counter
遍历字符串s,记当前字符为c,将counter[c] - 1
如果c已经在栈stack中,继续遍历
将字符c与栈顶元素top进行比较,若top > c并且counter[top] > 0则弹栈,重复此过程
将c入栈
算法执行过程中,栈内元素尽可能的保持递增顺序
最后,栈中剩余元素即为所求字符串cnt[stk.back() - 'a']>0 mean there is the same char in the remaining string, so we can pop it out.
This implementation is 8ms.
string removeDuplicateLetters2(string s) { // O(N) N是字符串长度
vector<char> cnt(26, 0);//count of char in remaining string
string stk;
unordered_set<char> chars;// chars in stk
for_each(s.begin(), s.end(), [&](char c) {cnt[c - 'a']++; });
for (char c : s) {
if (chars.count(c) == 0) {
while (not stk.empty() and stk.back()>c and cnt[stk.back() - 'a']>0) {
chars.erase(stk.back());
stk.pop_back();
}
chars.insert(c); //
stk.push_back(c); //
}
--cnt[c - 'a'];
}
return stk;
} This one is much faster as it doesn’t maintain a set.(4ms)
This one is much faster as it doesn’t maintain a set.(4ms)
string removeDuplicateLetters(string s) { // O(NK)
vector<char> cnt(26, 0);//count of char in remaining string
string stk;
for_each(s.begin(), s.end(), [&](char c) {cnt[c - 'a']++; });
for (char c : s) {
//For small array, linear search is faster than set(hash calculation)!
if (stk.find(c) == stk.npos) {
while (not stk.empty() and stk.back()>c and cnt[stk.back() - 'a']>0)
stk.pop_back();
stk.push_back(c);
}
--cnt[c - 'a'];
}
return stk;
}12.2 636. Exclusive Time of Functions
Given the running logs of n functions that are executed in a nonpreemptive single threaded CPU, find the exclusive time of these functions.
Each function has a unique id, start from 0 to n-1. A function may be called recursively or by another function.
A log is a string has this format : function_id:start_or_end:timestamp. For example, “0:start:0” means function 0 starts from the very beginning of time 0. “0:end:0” means function 0 ends to the very end of time 0.
Exclusive time of a function is defined as the time spent within this function, the time spent by calling other functions should not be considered as this function’s exclusive time. You should return the exclusive time of each function sorted by their function id.
Example 1:
Input:
n = 2
logs =
["0:start:0",
"1:start:2",
"1:end:5",
"0:end:6"]
Output:[3, 4]
Explanation:
Function 0 starts at time 0, then it executes 2 units of time and reaches the end of time 1.
Now function 0 calls function 1, function 1 starts at time 2, executes 4 units of time and end at time 5.
Function 0 is running again at time 6, and also end at the time 6, thus executes 1 unit of time.
So function 0 totally execute 2 + 1 = 3 units of time, and function 1 totally execute 4 units of time.Note:
Input logs will be sorted by timestamp, NOT log id.
Your output should be sorted by function id, which means the 0th element of your output corresponds to the exclusive time of function 0.
Two functions won’t start or end at the same time.
Functions could be called recursively, and will always end.
1 <= n <= 100
https://leetcode.com/problems/exclusive-time-of-functions
对C++程序来说,这个题的难度居然很大部分是split string.因为C++没有split string的函数,要自己写!其他部分只要思路清楚即可.
class Solution{
public:
vector<int> exclusiveTime(int n, vector<string>& logs) {
vector<int> r(n);
stack<pair<int, int>> stk;
for(string s: logs){
auto p=s.find_first_of(':'); //
int idx=stoi(s.substr(0,p));
s.erase(0,p+1); //
if(s[0]=='s'){
s.erase(0,6);
int tm=stoi(s); //
if(!stk.empty()){
pair<int,int>& pr=stk.top();
r[pr.first]+=tm-pr.second;
pr.second=-1;
}
stk.push({idx,tm});
}else{ // end
s.erase(0,4);
int tm=stoi(s);
pair<int,int>& pr=stk.top();
r[pr.first]+=tm-pr.second+1;
stk.pop();
if(!stk.empty()){
stk.top().second = tm+1;
}
}
}
return r;
}
};12.3 640. Solve the Equation
Solve a given equation and return the value of x in the form of string “x=#value”. The equation contains only ‘+’, ‘-’ operation, the variable x and its coefficient.
If there is no solution for the equation, return “No solution”.
If there are infinite solutions for the equation, return “Infinite solutions”.
If there is exactly one solution for the equation, we ensure that the value of x is an integer.
Example 1:
Input: “x+5-3+x=6+x-2”
Output: “x=2”
Example 2:
Input: “x=x”
Output: “Infinite solutions”
Example 3:
Input: “2x=x”
Output: “x=0”
Example 4:
Input: “2x+3x-6x=x+2”
Output: “x=-1”
Example 5:
Input: “x=x+2”
Output: “No solution”
https://leetcode.com/problems/solve-the-equation
public String solveEquation(String equation) {
int[] res = evaluateExpression(equation.split("=")[0]),
res2 = evaluateExpression(equation.split("=")[1]);
res[0] -= res2[0];
res[1] = res2[1] - res[1];
if (res[0] == 0 && res[1] == 0) return "Infinite solutions";
if (res[0] == 0) return "No solution";
return "x=" + res[1]/res[0];
}
public int[] evaluateExpression(String exp) {
String[] tokens = exp.split("(?=[-+])");
int[] res = new int[2];
for (String token : tokens) {
if (token.equals("+x") || token.equals("x")) res[0] += 1;
else if (token.equals("-x")) res[0] -= 1;
else if (token.contains("x")) res[0] +=
Integer.parseInt(token.substring(0, token.indexOf("x")));
else res[1] += Integer.parseInt(token);
}
return res;
}https://leetcode.com/problems/solve-the-equation/discuss/105311/Concise-Java-Solution
12.4 638. Shopping Offers
In LeetCode Store, there are some kinds of items to sell. Each item has a price.
However, there are some special offers, and a special offer consists of one or more different kinds of items with a sale price.
You are given the each item’s price, a set of special offers, and the number we need to buy for each item. The job is to output the lowest price you have to pay for exactly certain items as given, where you could make optimal use of the special offers.
Each special offer is represented in the form of an array, the last number represents the price you need to pay for this special offer, other numbers represents how many specific items you could get if you buy this offer.
You could use any of special offers as many times as you want.
Example 1:
Input: [2,5], [[3,0,5],[1,2,10]], [3,2]
Output: 14
Explanation:
There are two kinds of items, A and B. Their prices are $2 and $5 respectively.
In special offer 1, you can pay $5 for 3A and 0B
In special offer 2, you can pay $10 for 1A and 2B.
You need to buy 3A and 2B, so you may pay $10 for 1A and 2B (special offer #2), and $4 for 2A.
Example 2:
Input: [2,3,4], [[1,1,0,4],[2,2,1,9]], [1,2,1]
Output: 11
Explanation:
The price of A is $2, and $3 for B, $4 for C.
You may pay $4 for 1A and 1B, and $9 for 2A ,2B and 1C.
You need to buy 1A ,2B and 1C, so you may pay $4 for 1A and 1B (special offer #1), and $3 for 1B, $4 for 1C.
You cannot add more items, though only $9 for 2A ,2B and 1C.
Note:
There are at most 6 kinds of items, 100 special offers.
For each item, you need to buy at most 6 of them.
You are not allowed to buy more items than you want, even if that would lower the overall price.
https://leetcode.com/problems/shopping-offers
对于这种选择下一步怎么走的问题,可以用DFS解决,同时还可以求得可行解的路径. 这个问题相当于求combination with replacement.
一般的candidate都会想到这一步,下一步如何implement DFS是本题的难点. 如果把price信息处理之后放入那个special offers vector,用DFS的模板代码实现就很容易了. 代码如下:
struct Solution {
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs) {
int L=price.size();
for(int i=0;i<L;++i){
vector<int> t(L+1);
t[i]=1, t.back()=price[i];
special.push_back(t);
}
int r=INT_MAX;
dfs(special, needs, 0, r);
return r;
}
bool all0(vector<int>& v){for(int i:v) if(i) return 0; return 1;}
bool nega(vector<int>& v){for(int i:v) if(i<0) return 1; return 0;}
void dfs(vector<vector<int>>& special, vector<int>& needs, int cost, int& r){
if(all0(needs)){r=min(r, cost); return;}
if(nega(needs)) return;
for(auto& s: special){
if(cost+s.back()>r) continue;
for(int i=0;i<s.size()-1;++i) needs[i]-=s[i];
dfs(special, needs, cost+s.back(), r);
for(int i=0;i<s.size()-1;++i) needs[i]+=s[i];
}
}
};但是这个解法会TLE,对example 1,dfs函数会被调用55次,复杂度实在是太高了.上面的代码把所有的价格都看成special offer,没有利用special offer的特点,所以很慢.我们知道如果没有special offer的话,普通价格是多少,而这个价格可以作为一个上限.我们可以先对special offer做DFS,然后剩下的不能用special offer解决的needs再用普通的price计算,这样就可以得到最优解了.
 下面的DFS构造得就很精巧,对example 1,dfs函数会被调用4次,顺利过大集合.
下面的DFS构造得就很精巧,对example 1,dfs函数会被调用4次,顺利过大集合.
struct Solution { // 9ms
int shoppingOffers(vector<int>& price, vector<vector<int>>& special, vector<int>& needs, int cost = 0) {
if (any_of(needs.begin(), needs.end(),[](int i){return i<0;}))
return INT_MAX;
int m = cost + inner_product(needs.begin(),needs.end(), price.begin(), 0);
for (auto &offer : special) {
if (cost + offer.back() >= m) continue;// pruning
transform(needs.begin(), needs.end(), offer.begin(), needs.begin(),minus<int>());
m = min(m, shoppingOffers(price, special, needs, cost + offer.back()));
transform(needs.begin(), needs.end(), offer.begin(), needs.begin(),plus<int>());
}
return m;
}
};这个解法可圈点的地方还有transform, minus, plus, any_of, inner_product的使用.可以看出candidate对STL和C++的使用非常熟练.同时使用了默认构造函数简化编码.
12.5 84. Largest Rectangle in Histogram
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
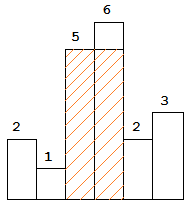
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given heights = [2,1,5,6,2,3],
return 10.
https://leetcode.com/problems/largest-rectangle-in-histogram/
http://jefflai.org/2017/06/13/84-Largest-Rectangle-in-Histogram/
http://blog.csdn.net/u013027996/article/details/43198421 说得非常详细
Use non-descending stack…递增栈
int largestRectangleArea(vector<int> &h) {
stack<int> S;
h.push_back(0);
int sum = 0;
for (int i = 0; i < h.size(); i++) {
if (S.empty() || h[i] > h[S.top()]) S.push(i);
else {
int tmp = S.top();
S.pop();
sum = max(sum, h[tmp]*(S.empty()? i : i-S.top()-1));
i--;
}
}
return sum;
} 这个解法如何证明呢?
12.6 218. The Skyline Problem
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B). Buildings Skyline Contour
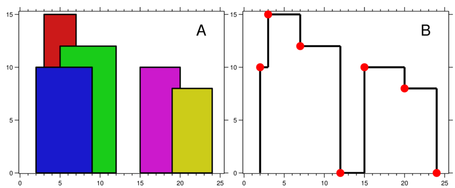
The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of “key points” (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], … ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
https://leetcode.com/problems/the-skyline-problem
http://bit.ly/2gTLITT, http://bit.ly/2gSPg8C
如果按照一个矩形一个矩形来处理将会非常麻烦,我们可以把这些矩形拆成两个点,一个左上顶点,一个右上顶点.将所有顶点按照横坐标排序后,我们开始遍历这些点.遍历时,通过一个堆来得知当前图形的最高位置.堆顶是所有顶点中最高的点,只要这个点没被移出堆,说明这个最高的矩形还没结束.对于左顶点,我们将其加入堆中.对于右顶点,我们找出堆中其相应的左顶点,然后移出这个左顶点,同时也意味这这个矩形的结束.具体代码中,为了在排序后的顶点列表中区分左右顶点,左顶点的值是正数,而右顶点值则存的是负数. 注意,堆中先加入一个零点高度,帮助我们在只有最矮的建筑物时选择最低值.

Because in C++ STL, priority_queue cannot erase element, we use multiset here:
#define PII pair<int,int>
class Solution {
public:
vector<pair<int, int>> getSkyline(vector<vector<int>>& buildings) {
vector<PII> r, h;
for(auto& b: buildings)
h.emplace_back(b[0],-b[2])/*start*/, h.emplace_back(b[1],b[2])/*end*/;
sort(h.begin(), h.end());//
multiset<int,greater<int>> m={0};
int prev=0;
for(PII &p: h){
if(p.second<0)
m.insert(-p.second); // start... add height
else
m.erase(m.find(p.second)); //end...remove height
int mx=*m.begin();
if(prev != mx)
r.emplace_back(p.first, mx), prev=mx;
}
return r;
}
};Similar to meeting room problem, when a starting point and a ending point overlaps, we should not consider this point, so we need to check the starting point first! Or we will get wrong result like the following:
Input:[[0,2,3],[2,5,3]]
Output:[[0,3],[2,0],[2,3],[5,0]]
Expected:[[0,3],[5,0]]12.7 224. Basic Calculator
Implement a basic calculator to evaluate a simple expression string.
The expression string may contain open ( and closing parentheses ), the plus + or minus sign -, non-negative integers and empty spaces .
You may assume that the given expression is always valid.
Some examples:
"1 + 1" = 2
" 2-1 + 2 " = 3
"(1+(4+5+2)-3)+(6+8)" = 23https://leetcode.com/problems/basic-calculator/
http://www.cnblogs.com/grandyang/p/4570699.html
这道题让我们实现一个基本的计算器来计算简单的算数表达式,而且题目限制了表达式中只有加减号,数字,括号和空格,没有乘除,那么就没啥计算的优先级之分了.于是这道题就变的没有那么复杂了.我们需要一个栈来辅助计算,用个变量sign来表示当前的符号,我们遍历给定的字符串s,如果遇到了数字,由于可能是个多位数,所以我们要用while循环把之后的数字都读进来,然后用sign*num来更新结果res;如果遇到了加号,则sign赋为1,如果遇到了符号,则赋为-1;如果遇到了左括号,则把当前结果res和符号sign压入栈,res重置为0,sign重置为1;如果遇到了右括号,结果res乘以栈顶的符号,栈顶元素出栈,结果res加上栈顶的数字,栈顶元素出栈.
class Solution {
public:
int calculate(string s) {
int res = 0, sign = 1, n = s.size();
stack<int> st;
for (int i = 0; i < n; ++i) {
char c = s[i];
if (c >= '0') {
int num = 0;
while (i < n && s[i] >= '0') {
num = 10 * num + s[i++] - '0';
}
res += sign * num;
--i;
} else if (c == '+') {
sign = 1;
} else if (c == '-') {
sign = -1;
} else if (c == '(') {
st.push(res);
st.push(sign);
res = 0;
sign = 1;
} else if (c == ')') {
res *= st.top(); st.pop();
res += st.top(); st.pop();
}
}
return res;
}
};12.8 227. Basic Calculator II
Implement a basic calculator to evaluate a simple expression string.
The expression string contains only non-negative integers, +, -, *, / operators and empty spaces . The integer division should truncate toward zero.
You may assume that the given expression is always valid.
Some examples:
"3+2*2" = 7
" 3/2 " = 1
" 3+5 / 2 " = 5https://leetcode.com/problems/basic-calculator-ii/
这道题是之前那道Basic Calculator 基本计算器的拓展,不同之处在于那道题的计算符号只有加和减,而这题加上了乘除,那么就牵扯到了运算优先级的问题,好在这道题去掉了括号,还适当的降低了难度,估计再出一道的话就该加上括号了.不管那么多,这道题先按木有有括号来处理,由于存在运算优先级,我们采取的措施是使用一个栈保存数字,如果该数字之前的符号是加或减,那么把当前数字压入栈中,注意如果是减号,则加入当前数字的相反数,因为减法相当于加上一个相反数.如果之前的符号是乘或除,那么从栈顶取出一个数字和当前数字进行乘或除的运算,再把结果压入栈中,那么完成一遍遍历后,所有的乘或除都运算完了,再把栈中所有的数字都加起来就是最终结果了.
class Solution {
public:
int calculate(string s) {
int res = 0, d = 0;
char sign = '+';
stack<int> nums;
for (int i = 0; i < s.size(); ++i) {
if (s[i] >= '0') {
d = d * 10 + s[i] - '0';
}
if ((s[i] < '0' && s[i] != ' ') || i == s.size() - 1) {
if (sign == '+') nums.push(d);
if (sign == '-') nums.push(-d);
if (sign == '*' || sign == '/') {
int tmp = sign == '*' ? nums.top() * d : nums.top() / d;
nums.pop();
nums.push(tmp);
}
sign = s[i];
d = 0;
}
}
while (!nums.empty()) {
res += nums.top();
nums.pop();
}
return res;
}
};12.8.1 RPN and Shunting Yard
class Solution(object):
def evalRPN(self, RPN):
stack = []
for i in range(len(RPN)):
if RPN[i] not in '+-*/':
stack.append(int(RPN[i]))
else:
r = stack.pop()
if RPN[i] == '+':
stack[-1] += r
elif RPN[i] == '-':
stack[-1] -= r
elif RPN[i] == '*':
stack[-1] *= r
elif RPN[i] == '/':
stack[-1] /= r
return stack[-1]
def ShuntingYard(self, s):
stack, RPN, j = [], [], 0
while j < len(s):
if s[j].isdigit():
i = j
while j < len(s) and s[j].isdigit():
j += 1
RPN.append(s[i:j])
else:
if s[j] in '+-':
while stack and stack[-1] != '(':
RPN.append(stack.pop())
stack.append(s[j])
elif s[j] in '*/':
while stack and stack[-1] not in '(+-':
RPN.append(stack.pop())
stack.append(s[j])
elif s[j] == '(':
stack.append(s[j])
elif s[j] == ')':
while stack[-1] != '(':
RPN.append(stack.pop())
stack.pop()
j += 1
while stack:
RPN.append(stack.pop())
return RPN
def calculate(self, s):
RPN = self.ShuntingYard(s)
return self.evalRPN(RPN)12.9 32. Longest Valid Parentheses
Given a string containing just the characters ‘(’ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.
Example 1:
Input: “(()” Output: 2 Explanation: The longest valid parentheses substring is “()” Example 2:
Input: “)()())” Output: 4 Explanation: The longest valid parentheses substring is “()()”
https://leetcode.com/problems/longest-valid-parentheses/
class Solution {
public:
int longestValidParentheses(string s) {
stack<int> stk;
stk.push(-1);
int r=0;
for(int i=0;i<s.size();i++){
if(s[i]=='(') stk.push(i);
else{
if(stk.top()>=0 and s[stk.top()]=='('){
stk.pop();
r=max(r, i-stk.top());
}else
stk.push(i);
}
}
return r;
}
};Use stack or DFS for this kind of parenthese problem.