Chapter 18 Other Trees
18.1 AVL Tree
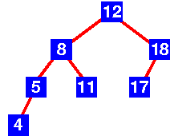
AVL Tree
2017(4-6月) 码农类 硕士 全职 Yahoo - 内推 - Onsite |Otherfresh grad应届毕业生
刚面完 ads组 感觉这个onsite还是挺难的
round1(国人大哥):
(大哥上来问 为啥大家都从Yahoo往外跳 我还会来面试 问得我也是一脸懵逼…我能说是因为有食堂的并且还在招人的公司不多了么)
os知识 + 生产者消费者问题(多线程) + base64 输入一个string 本来每个char用8bits表示 然后换成用6bits表示之后返回新的string(逻辑比较复杂写的有点乱- -)
round2:(三哥)
给一个unsorted vector 生成一个balanced bst(在电脑上写的 跑testcase 自己写treenode)
实现AVLtree (MD没错 就是实现一个自平衡的AVL tree)实在是太过分了!没写完
round3:(国人大哥)
先是俩脑筋急转弯一样的问题吧 (据说要用染色方法来做).re.
给一个N(N = 2 * k)*N的矩阵 扣掉左上角右下角 还能用一个1 * 2的小矩阵来覆盖完整么? 后来在提示下用染色的逻辑来考虑的…
给一个N*N的矩阵 扣掉左上角 可以用一个L形的矩阵来覆盖么…我觉得很intuitive的可以啊
设计一个database table 有用户 订单 物品 没准备过database的设计 随便画了一下…
给一个array unsorted,可以有重复的情况每次merge两个数 再放回去 每一次merge的cost是俩数的和 求merge成一个数的最小cost 我觉得贪心可以做 用一个heap 每次merge最小的
然后问heap是怎么实现的啊 要是去掉某一个元素咋做啊 我说和最后一个交换 然后除掉 然后swap下来….
第二轮第一问确实是 sort + recursion建树
follow up就是写AVL 每次一个node一个node这样插 过程始终保持balanced
http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=276467
非常详细的介绍:
http://www.cnblogs.com/skywang12345/p/3577360.html
http://www.growingwiththeweb.com/data-structures/avl-tree/overview/
- Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2Update height: y, z
b) Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2- Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4Update height: y, z
d) Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4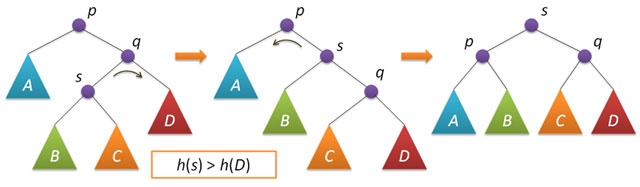
基本操作就是left rotation和right rotation. 注意叶子节点(子树)的高度不需要更新.
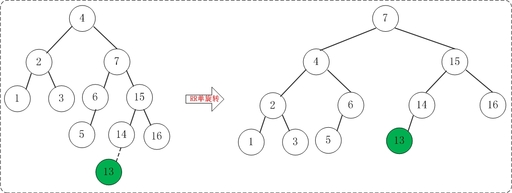
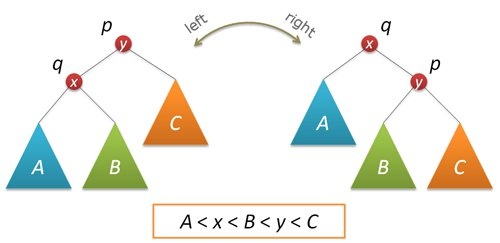
// An AVL tree node
struct Node{
Node *left, *right;
int h, key;
Node(int k):key(k),right(0),left(0),h(1){}
};
int height(Node *N) { if (N == NULL) return 0; return N->h; }
Node* insert(Node* node, int key) {
/* 1. Perform the normal BST insertion */
if (node == NULL) return(new Node(key));
if (key < node->key) node->left = insert(node->left, key);
else if (key > node->key) node->right = insert(node->right, key);
else return node; // Equal keys are not allowed in BST
return balance(node);
}
Node* balance(Node *node){
/* 2. Update height of this ancestor node */
node->h = 1 + max(height(node->left), height(node->right));
/* 3. Get the balance factor of this ancestor node to check whether this node became unbalanced */
int bfactor = height(node->left) - height(node->right);
// If this node becomes unbfactord, then there are 4 cases
if (bfactor > 1 && key < node->left->key) // (a)Left Left Case
return rightRotate(node);
if (bfactor > 1 && key > node->left->key) { // (b)Left Right Case
node->left = leftRotate(node->left);
return rightRotate(node);
}
if (bfactor < -1 && key > node->right->key) // (c)Right Right Case
return leftRotate(node);
if (bfactor < -1 && key < node->right->key) { // (d)Right Left Case
node->right = rightRotate(node->right);
return leftRotate(node);
}
return node; /* return the (unchanged) node pointer */
}
Node *rightRotate(Node *y) {
Node *x = y->left;
Node *t = x->right;
// Perform rotation
x->right = y, y->left = t;
// Update heights
y->h = max(height(y->left), height(y->right))+1;
x->h = max(height(x->left), height(x->right))+1;
return x; // Return new root
}leftRotate道理是一样的,只是左右互换,这里就不写了.
-
Comparison with Red Black Tree
The AVL tree and other self balancing search trees like Red Black are useful to get all basic operations done in O(Log n) time. The AVL trees are more balanced compared to Red Black Trees, but they may cause more rotations during insertion and deletion. So if your application involves many frequent insertions and deletions, then Red Black trees should be preferred. And if the insertions and deletions are less frequent and search is more frequent operation, then AVL tree should be preferred over Red Black Tree.
18.2 Interval Tree
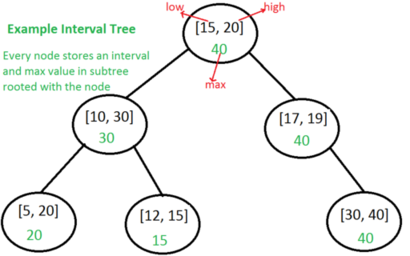
interval trichotomy(CLRS p348.):
1. Partial Overlap; 2. Total Overlap; 3.No Overlap
18.3 Segement Tree
http://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/
A segment tree is a tree data structure for storing intervals, or segments. It allows faster querying (e.g sum or min) in these intervals. Lazy propagation is useful when there are high number of updates in the input array.
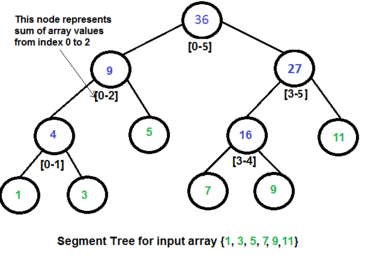
Create segment tree in array like heap in \(O(N)\).
LChild: \(2i+1\)
RChild: \(2i+2\)
Parent: \((i-1)/2\)
感觉segment tree和winner tree很像,都是原数组元素是叶节点.
//O(N)
void construct_segment_tree(){}
OJ:
http://www.spoj.pl/problems/BRCKTS/
http://www.spoj.com/problems/GSS3/
http://www.spoj.com/problems/HORRIBLE
http://www.spoj.pl/problems/IOPC1207/
http://www.spoj.com/problems/GSS2/
http://www.spoj.com/problems/SEGSQRSS/
http://www.spoj.com/problems/ORDERSET/
http://www.spoj.com/problems/HELPR2D2/
http://www.spoj.com/problems/TEMPLEQ
18.3.1 Lazy Propagation in Segment Tree
http://www.geeksforgeeks.org/lazy-propagation-in-segment-tree/
https://www.lintcode.com/en/problem/segment-tree-build/
https://www.lintcode.com/en/problem/segment-tree-build-ii/
struct Solution {
SegmentTreeNode * build(vector<int>& v) {
return rec(v, 0, v.size()-1);
}
SegmentTreeNode* rec(vector<int>& v, int h, int t){
if(h>t) return 0;
SegmentTreeNode* n=new SegmentTreeNode(h,t);
if(h<t){
n->left = rec(v, h, h+(t-h)/2);
n->right = rec(v, h+(t-h)/2+1, t);
n->max = max(n->left->max, n->right->max);
} else
n->max = v[h];
return n;
}
};https://www.lintcode.com/en/problem/segment-tree-modify/
struct Solution {
void modify(SegmentTreeNode *root, int index, int value) {
if(!root) return;
if(root->start==root->end){ root->max=value; return; }
modify((index <= root->left->end)? root->left: root->right, index, value);
root->max = max(root->left->max, root->right->max);
}
};https://www.lintcode.com/en/problem/segment-tree-query/
struct Solution {
int query(SegmentTreeNode *root, int start, int end) {
if(!root || end<root->start || start>root->end) return 0;
if(start<=root->start && root->end <= end) return root->max;
return max(query(root->left,start,end), query(root->right,start,end));
}
};18.4 Interval Sum
https://www.lintcode.com/en/problem/interval-sum/
这题是静态数据,用cumulative sum也可以做到\(O(N)\).
struct node{
int h, t;
long long sum;
node *l, *r;
node(int h_,int t_,long long sum_):h(h_),t(t_),sum(sum_),l(0),r(0){}
};
node* build_tree(vector<int>& v, int h, int t){
if(h==t) return new node(h,t,v[h]);
int m=h+(t-h)/2;
node *l = build_tree(v,h,m);
node *r = build_tree(v,m+1,t);
node *R = new node(h,t,l->sum+r->sum);
R->l=l, R->r=r;
return R;
}
long long query(node* R, int h, int t){
if(R && h>R->t || t<R->h) return 0;
if(h <= R->h && t >= R->t) return R->sum;
return query(R->l,h,t)+query(R->r,h,t);
}
struct Solution {
vector<long long> intervalSum(vector<int> &A, vector<Interval> &queries) {
node* R=build_tree(A,0,A.size()-1);
vector<long long> res;
for(auto i: queries) res.push_back(query(R,i.start,i.end));
return res;
}
};18.5 Interval Sum II
https://www.lintcode.com/en/problem/interval-sum-ii/
struct node{
int h, t;
long long sum;
node *l, *r;
node(int h_,int t_,long long sum_):h(h_),t(t_),sum(sum_),l(0),r(0){}
};
node* build_tree(vector<int>& v, int h, int t){
if(h>t) return 0;
if(h==t) return new node(h,t,v[h]);
int m=h+(t-h)/2;
node *l = build_tree(v,h,m);
node *r = build_tree(v,m+1,t);
node *R = new node(h,t,l->sum+r->sum);
R->l=l, R->r=r;
return R;
}
long long query(node* R, int h, int t){
if(!R) return 0;
if(R && h>R->t || t<R->h) return 0;
if(h <= R->h && t >= R->t) return R->sum;
return query(R->l,h,t)+query(R->r,h,t);
}
struct Solution {
node* R;
Solution(vector<int> A) {
R=build_tree(A,0,A.size()-1);
}
long long query(int start, int end) {
return ::query(R,start,end);
}
void modify(int index, int value) {
_modify(R,index,value);
}
void _modify(node* n, int i, int val){
if(!n) return;
if(n->h==n->t){n->sum=val; return;} // i==n->h/t
int m=n->h + (n->t - n->h)/2;
_modify(i<=m?n->l:n->r,i,val);
n->sum=n->l->sum + n->r->sum;
}
};18.6 Interval Minimum Number
https://www.lintcode.com/en/problem/interval-minimum-number/
18.7 Count of Smaller Number
https://www.lintcode.com/en/problem/count-of-smaller-number/
Algo: Binary Search
18.8 Count of Smaller Number before itself
https://www.lintcode.com/en/problem/count-of-smaller-number-before-itself/
Give you an integer array (index from 0 to n-1, where n is the size of this array, data value from 0 to 10000) . For each element A[i] in the array, count the number of element before this element A[i] is smaller than it and return count number array.
http://www.jianshu.com/p/a2aae061d637
https://zhengyang2015.gitbooks.io/lintcode/count_of_smaller_number_before_itself_249.html
https://github.com/shawnfan/LintCode/blob/master/Java/Count%20of%20Smaller%20Number%20before%20itself.java
18.9 315. Count of Smaller Numbers After Self
https://leetcode.com/problems/count-of-smaller-numbers-after-self/
http://www.szeju.com/index.php/other/28230340.html
https://github.com/shadowwalker2718/LeetCode/blob/master/C++/count-of-smaller-numbers-after-self.cpp
18.10 Binary Index Tree
BIT actually are the binomial trees. and has two symetric trees!!!
Update is to climb up, Query is to step down!!!
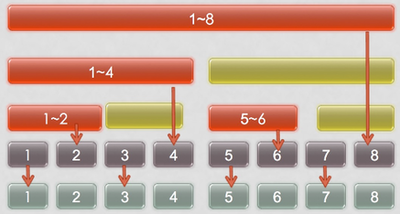
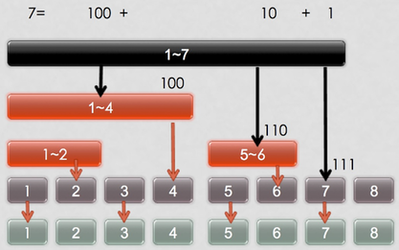
http://mengyou0304.github.io/2015/08/11/Binary%20IndexedTree/
https://kartikkukreja.wordpress.com/2013/12/02/range-updates-with-bit-fenwick-tree/
规律:
- 奇数点全部存原数组值
- 偶数点K存入的位数与K&(-K)后面的0相关,有M个0就存1<<M个数字
18.11 307. Range Sum Query - Mutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive. The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.
https://leetcode.com/problems/range-sum-query-mutable/
#define LB(x) (x&-x)
struct NumArray {
vector<int> B; // to store BIT
vector<int> N; // to store original tree
NumArray(const vector<int> &nums) {
B.resize(nums.size()+1);
N=B;
for(int i=0; i<nums.size(); i++)
update(i, nums[i]);
}
void update(int i, int val) { // point update
int k = i+1;
int delta = val - N[k];
while (k < B.size())
B[k] += delta, k += LB(k);
N[i+1] = val; // store the value of original array in N
}
int sumRange(int i, int j) { return _getSum(j+1) - _getSum(i); }
int _getSum(int k) { // k is index of `B`
int r = 0;
while(k>0)
r += B[k], k -= LB(k);
return r;
}
};Note
:
BandNuse 1 as the start index, so the length of theBandNare 1 greater than original arraynums.
kis index of binary_index_tree array,iandjare index of original array.
- Can we just use BIT array
Band throw the original arrayN?
No! The algorithm needs two arrays. The original arrayNand binary_index_tree arrayB.
sumRangeis inclusive. So it isgetSum(k=j+1) - getSum(k=i).
18.12 308. Range Sum Query 2D - Mutable
Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).
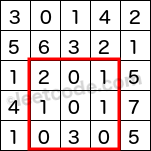
Range Sum Query 2D - Mutable
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10https://leetcode.com/problems/range-sum-query-2d-mutable/
http://www.cnblogs.com/grandyang/p/5300458.html
2D BIT
Paper: BIT D-dimension
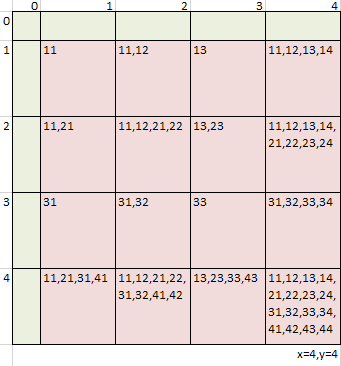
struct NumMatrix { // Binary Indexed Tree
NumMatrix(const vector<vector<int>> &matrix) {
if (matrix.empty() || matrix[0].empty()) return;
mat.resize(matrix.size() + 1, vector<int>(matrix[0].size() + 1));
bit.resize(matrix.size() + 1, vector<int>(matrix[0].size() + 1));
for (int i = 0; i < matrix.size(); ++i)
for (int j = 0; j < matrix[i].size(); ++j)
update(i, j, matrix[i][j]);
}
void update(int row, int col, int val) {
int diff = val - mat[row + 1][col + 1]; ////
for (int i = row + 1; i < mat.size(); i += i&-i)//
for (int j = col + 1; j < mat[i].size(); j += j&-j)
bit[i][j] += diff;
mat[row + 1][col + 1] = val;
}
int sumRegion(int row1, int col1, int row2, int col2) {
return getSum(row2 + 1, col2 + 1) - getSum(row1, col2 + 1)
- getSum(row2 + 1, col1) + getSum(row1, col1);
}
int getSum(int row, int col) {
int res = 0;
for (int i = row; i > 0; i -= i&-i)
for (int j = col; j > 0; j -= j&-j)
res += bit[i][j];
return res;
}
private:
vector<vector<int>> mat; // original matrix
vector<vector<int>> bit; // binary index tree
};18.12.1 Range Updates and Point queries
http://www.spoj.com/problems/UPDATEIT/
https://programmingcontests.quora.com/Tutorial-Range-Updates-in-Fenwick-Tree
18.13 303. Range Sum Query - Immutable
https://leetcode.com/problems/range-sum-query-immutable/
18.13.1 Distributed BIT
Be able to reach T: \(Log(LogN)\)
An Enhanced Distributed System to improve the Time Complexity of Binary Indexed Trees
More Exercises: https://a2oj.com/Category.jsp?ID=26
What is the difference between a binary indexed tree and a segment tree?
A Binary Indexed Tree (BIT) is used to store cumulative sums. You have an array a0,a1,…,an. You want to be able to retrieve the sum of the first k elements in O(logn) time, and you want to be able to add a quantity q to the i-th element in O(logn) time. Note that these two operations can be implemented with a normal array, but the time complexity will be O(n) and O(1).
A segment tree (sometimes called range tree) is a much more flexible data structure, you can use it to store many different things. You have an array a0,a1,…,an. You want to be able to retrieve the sum (or the maximum, or the minimum, or the greatest common divisor, or another associative function) of the elements between the l-th and the r-th in O(logn) time, and you want to be able to add (or to overwrite, or to multiply by…) a quantity q to the i-th element (or to every element between the l-th and the r-th) in O(logn) time.
Segment trees (as well as BITs) can be generalized to k dimensions. Often a problem will require you to implement a 2d segment tree (or BIT).
It is possible to simulate a BIT using a segment tree, so you might ask: why would you prefer a BIT over a segment tree? Well, a BIT is much easier to code and requires less memory. So if a BIT is enough to solve the problem, go for it, else try with a segment tree.
18.17 Spanning Tree
From man brctl:
SPANNING TREE PROTOCOL
Multiple ethernet bridges can work together to create even larger networks
of ethernets using the IEEE 802.1d spanning tree protocol. This protocol is
used for finding the shortest path between two ethernets, and for eliminat‐
ing loops from the topology. As this protocol is a standard, linux bridges
will interwork properly with other third party bridge products. Bridges
communicate with each other by sending and receiving BPDUs (Bridge Protocol
Data Units). These BPDUs can be recognised by an ethernet destination
address of 01:80:c2:00:00:00.18.18 671. Second Minimum Node In a Binary Tree
Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes.
Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.
If no such second minimum value exists, output -1 instead.
Example 1:
Input:
2
/ \
2 5
/ \
5 7Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.
Example 2:
Input:
2
/ \
2 2Output: -1
Explanation: The smallest value is 2, but there isn’t any second smallest value.
https://leetcode.com/problems/second-minimum-node-in-a-binary-tree
18.18.2 Algo 2: Tournament Tree Finding
struct Solution {
int findSecondMinimumValue(TreeNode* R) {
if(!R || !R->left && !R->right) return -1; // empty or leaf node
if(R->right->val==R->left->val){
int l=findSecondMinimumValue(R->left);
int r=findSecondMinimumValue(R->right);
if(l==-1 and r==-1) return -1;
else if(l>0 and r>0) return min(r,l);
if(l==-1) return r; return l;
}
if(R->val==R->left->val){
int t=findSecondMinimumValue(R->left);
return t==-1?R->right->val:min(t,R->right->val);
}else if(R->val==R->right->val){
int t=findSecondMinimumValue(R->right);
return t==-1?R->left->val:min(t,R->left->val);
}
}
};The corner case R->right->val==R->left->val must be processed by a separate logic. Both algos have the same time complexity, but the second one has smaller constant coefficient.
Reference: Tournament Tree