Chapter 27 Select Topics
27.2 200. Number of Islands
 https://leetcode.com/problems/number-of-islands/
https://leetcode.com/problems/number-of-islands/
27.2.1 Iterative
struct Solution {
int numIslands(vector<vector<char>>& grid) {
int r = 0;
if (grid.empty() || grid[0].empty()) return r;
const vector<pair<int, int>> D = { { 1,0 },{ -1,0 },{ 0,1 },{ 0,-1 } };
int R = grid.size(), C = grid[0].size();
vector<vector<bool>> vd(R, vector<bool>(C));
for(int i=0;i<R;i++){
for(int j=0;j<C;j++){
if (vd[i][j] || grid[i][j]=='0'){ continue; }
stack<pair<int, int>> stk;
stk.emplace(i,j), vd[i][j]=true;
while (!stk.empty()) {
auto p = stk.top(); stk.pop();
for (auto d : D) {
int x = p.first + d.first, y = p.second + d.second;
if (x >= 0 && x < R && y >= 0 && y < C && !vd[x][y]) {
if (grid[x][y]=='1')
stk.emplace(x, y), vd[x][y] = true;
}
}
}
r++;
}
}
return r;
}
};小心while loop中的continue!!!
27.2.2 Recursive
struct Solution {
const vector<pair<int,int>> D = {{1,0},{-1,0},{0,1},{0,-1}};
int numIslands(vector<vector<char>>& grid) {
if (grid.empty() || grid[0].empty()) return 0;
int r = 0, R = grid.size(), C = grid[0].size();
vector<vector<char>> bm(R, vector<char>(C));
for(int i=0;i<R;++i){
for(int j=0;j<C;++j){
if (!bm[i][j]++ and grid[i][j]=='1')
dfs(grid, i, j, bm, R, C), ++r;
}
}
return r;
}
void dfs(vector<vector<char>>&grid, int i, int j,
vector<vector<char>>& bm, int ROW, int COL)
{
for(auto d: D){
int x = i + d.first, y = j + d.second;
if (x>=0 && y>=0 && x<ROW && y<COL && !bm[x][y]++){
if(grid[x][y]=='1')
dfs(grid, x, y, bm, ROW, COL), bm[i][j]++;
}
}
}
};The reason I use vector<vector<char>> here is to avoid forgetting to set bm value true by using !bm[x][y]++.
27.2.3 BFS
BFS only has iterative version.
struct Solution {
int numIslands(vector<vector<char>>& grid) { // T: O(*), S: O(*)
if (grid.empty() or grid[0].empty()) return 0;
const vector<pair<int,int>> dir={{1,0},{-1,0},{0,1},{0,-1}};
int R=grid.size(), C=grid[0].size() ,r=0;
vector<vector<bool>> visited(R,vector<bool>(C));
for(int i=0;i<R;++i){
for(int j=0;j<C;++j){
if(visited[i][j] or grid[i][j]=='0') continue;
visited[i][j]=true;
queue<pair<int,int>> q;
q.emplace(i,j);
while(!q.empty()){
int sz=q.size();
while(sz--){
auto t=q.front(); q.pop();
for(auto d: dir){
int nx=t.first+d.first, ny=t.second+d.second;
if(nx>=0 and nx<R and ny>=0 and ny<C and !visited[nx][ny]){
visited[nx][ny]=true;
if(grid[nx][ny]=='1')
q.emplace(nx, ny);
}
}
}
}
r++;
}
}
return r;
}
};27.2.4 Union Find
#include <numeric>
class Solution {
public:
vector<int> bo, sz;
void makeset(int len) {
bo.resize(len),sz.resize(len);
iota(bo.begin(), bo.end(), 0);
fill(sz.begin(), sz.end(), 1);
}
int findset(int x) {
return (x==bo[x])?x:findset(bo[x]);
};
void merge(int x, int y) {
int bo1 = findset(x), bo2 = findset(y);// after this line, no x and y any more!!
if (bo1 == bo2) { return; }
if(bo1<bo2) swap(bo1,bo2);
bo[bo2]=bo1,sz[bo1]+=sz[bo2],sz[bo2]=0;
};
int numIslands(vector<vector<char>>& grid) {
if (grid.empty() || grid[0].empty()) return 0;
const vector<pair<int, int>> DIR = {{ 0, -1 },{ -1,0 },{ 1,0 },{ 0,1 }};
const int ROW = grid.size(), COL = grid[0].size();
makeset(ROW*COL);
auto m2a = [COL](int x, int y) {return x*COL + y; };////
for (int i = 0; i<ROW; ++i) {
for (int j = 0; j<COL; ++j) {
int aidx = m2a(i, j);//array index
if (grid[i][j]=='0') {
sz[aidx] = 0;
continue;
}
for (auto d : DIR) {
int ni = i + d.first, nj = j + d.second;
int naidx = m2a(ni, nj);
if (ni >= 0 && ni<ROW && nj >= 0 && nj<COL && grid[ni][nj]=='1'){
merge(aidx, naidx);
}
}
}
}
return count_if(sz.cbegin(), sz.cend(), [](int i) {return i>0; });
}
};Another way to make set:
class Solution {
public:
vector<int> bo;
vector<int> sz;
void makeset(int len) {
bo.resize(len);
sz.resize(len);
fill(sz.begin(), sz.end(), 1);
fill(bo.begin(), bo.end(), -1);////
}
//// iterative way of findset
int findset(int x) {
while(-1 != bo[x]) {x = bo[x];}
return x;
};
//...
};findset的解释: 如果我没有boss(
bo[x]==-1),就返回我自己,否则返回我boss的boss,知道我的boss的boss没有boss(没有boss的就是超级大boss- root).
27.3 305. Number of Islands II
https://leetcode.com/problems/number-of-islands-ii/
这道题只有union find一条路了!
27.4 The Suspects
http://poj.org/problem?id=1611
http://www.cnblogs.com/cherish_yimi/archive/2009/10/11/1580849.html
#include<iostream>
using namespace std;
int n, m, i, j;
int rep[30005], num[30005];
void makeSet(int n){
for (i = 0; i < n; i++) rep[i] = i, num[i] = 1;
}
int findSet(int x){
if (rep[x] != x) rep[x] = findSet(rep[x]);
return rep[x];
}
void Union(int a, int b){
int x = findSet(a), y = findSet(b);// no a,b after this line
if (x == y){
return;
}
int sma = (num[x] <= num[y]) ? x : y;
int big = (sma == x) ? y : x;
rep[sma] = big;
num[big] += (num[sma]--);
}
int main(){
while (scanf("%d %d", &n, &m) != EOF && n != 0){
makeSet(n);
for (i = 0; i < m; i++){
int count, first, b;
scanf("%d %d", &count, &first);
for (j = 1; j < count; j++){
scanf("%d", &b);
Union(first, b);
}
}
printf("%d\n", num[findSet(0)]);
}
return 0;
}27.5 406. Queue Reconstruction by Height
Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers (h, k), where h is the height of the person and k is the number of people in front of this person who have a height greater than or equal to h. Write an algorithm to reconstruct the queue.
Note: The number of people is less than 1,100.
Example
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
 https://leetcode.com/problems/queue-reconstruction-by-height/
https://leetcode.com/problems/queue-reconstruction-by-height/
http://massivealgorithms.blogspot.com/2016/09/leetcode-406-queue-reconstruction-by.html
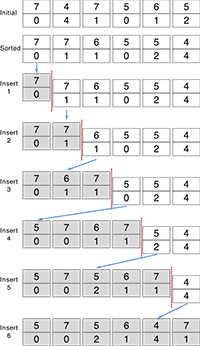
http://tianshilei.me/2016/10/19/leetcode406/
解法1:插入排序Insertion Sort
这道题就是一道排序题,只不过由于它的元素是 pair,因此排序的条件比较奇特.因此,我们需要使用的工具可以定下来了,就是使用 STL中的sort 函数,然后定义comp.
那我们如何定义这个comp呢?请先考虑,如果给定几张特殊的扑克牌,每张扑克牌上都有两个数字,分别代表题目中的 h 和 k,然后我们需要将这副牌按照题目的要求排列,那么应该如何手动做呢?我想,我应该会先按照 h 对手上的牌进行排序,从大到小.那如果 h 一样怎么办?那么谁的 k 小谁排在前面.这是第一轮排序.假设我的牌是从左向右排列的.然后从最左边一张牌开始,每次拿出来一张,看看它的 k 是多少,就将它插在从左数第 k 个位置,然后再取下一张,重复这个过程,直到所有的牌都重新插好.这是第二轮排序.我们就拿上面它给的例子来看:
我们通过最初的排序可以得到排序后的结果,然后再对每一张牌进行插入式排序.图中的蓝色箭头就代表我们将这张牌取出来,插到相应的位置.
那么接下来的问题是,我们为什么要按照上面说的规则进行第一轮排序呢?这个问题的回答其实需要参照我们第二轮插入的过程来看.我们在第二轮进行插入的时候,每次都是从最左边(也就是序列的初始位置)开始数第 k 个位置进行插入,这个有些贪心的策略在里面(而 Leetcode 上面也确实将这个题的 Tags 设置为 greedy),就是考虑所谓的局部最合适.因此,为了让后面的元素每次找插入位置的时候从最左边开始且恰好第 k 个位置之前的元素都要大于它,这需要我们在每次选择元素的时候按照 h 递减的次序选,因此才有了第一轮排序中的对 h 进行排序,大的放在前面这个策略了.我们第一轮排序中还有一个原则是,如果 h 一样,那么谁的 k 小谁排在前面.这个是为什么呢?举个反例就可以说明了.还看第二轮,假如 k 大的排在前面,那么我们首先会拿到大的那张牌C1,假设它的 k 值是 k1,然后将它插在第 k1 个位置,接下来我们会拿到小的那张牌C2,假设它的 k 值是 k2,且 k1 > k2,那么按照我们第二轮的插入策略,必然将它插在 C1 的前面,这个时候虽然 C2的 k 值是对着的,但是 C1 的值就不应该是 k1,而应该是 k1 + 1 了,就不对了.
有了上述手动排序的过程,我们就不难写出相应的 C++ 代码了,这里我们用了一些 C++11 新特性,比如 Lambda 表达式、auto 符号等.
学插入排序的时候觉得太简单没啥用,这道题就派上用场了.
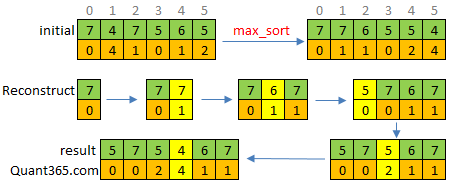
struct Solution { // 83 ms, O(N^2)
vector<pair<int, int>> reconstructQueue(vector<pair<int, int>>& people) {
sort(people.begin(), people.end(), [](const pair<int, int>& a,const pair<int, int>& b){
return (a.first > b.first) || ((a.first == b.first) && (a.second < b.second));
});
vector<pair<int, int>> r;
for(auto p : people) r.insert(r.begin() + p.second, p);
return r;
}
};解法2:
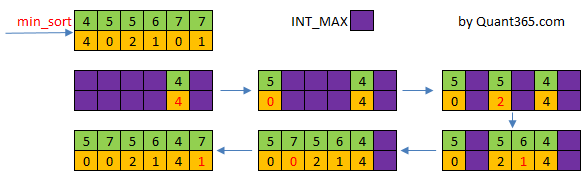
上面那种方法是简洁,但是用到了额外空间,我们来看一种不使用额外空间的解法.
解法3:
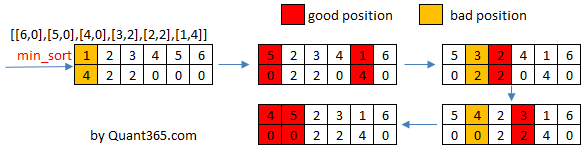
struct Solution { // O(N^2)
vector<pair<int, int>> reconstructQueue(vector<pair<int, int>>& people) {
sort(people.begin(), people.end(), [](const pair<int, int>& a, const pair<int, int>& b) {
return a.first > b.first || (a.first == b.first && a.second < b.second);
});
for (int i = 1; i < people.size(); ++i) {
int cnt = 0;
for (int j = 0; j < i; ++j) {
if (cnt == people[i].second) {
pair<int, int> t = people[i];
for (int k = i - 1; k >= j; --k)
people[k + 1] = people[k];
people[j] = t;
break;
}
if (people[j].first >= people[i].first) ++cnt;
}
}
return people;
}
};考点是sort的定制的写法,vector的insert函数用法.
复杂度: 插入排序是O(N^2),所以T始终是\(O(N^2)\), S可以降到\(O(1)\).