Chapter 68 Indeed
68.1 Unrolled Linked List
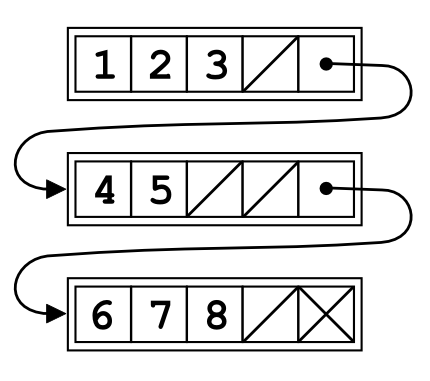
Unrolled_linked_lists.png
#ifndef APPLECPP_UNROLLEDLL_H
#define APPLECPP_UNROLLEDLL_H
#include <henry.h>
namespace _indeed_ULL{
struct node{
char v[5];
int num_char;
node* next=0;
};// null ended single linked list
struct unrolledLL{
unrolledLL():head(0),num_char(0){}
node* head;
int num_char;
char get(int i){// index
if(i<0 or i>=num_char){return '\0';}
node* c=head;
int start=0;// the first char's index in the node
while(c){ // index+length is index
if(i<=start+c->num_char and i>=start){
return c->v[i-start];
}else{
start+=c->num_char;
}
c=c->next;
}
return '\0';
}
//Insert需要考虑
//1.普通插进去.
//2.插入的node满了,要在后面加个node.
//3.插入的node是空的,那就要在尾巴上加个新node.
//还需要考虑每个node的len,以及totalLen的长度变化.
bool insert(char ch, int i){
if(i<0 or i>num_char) return false;
node* cur=head;
int start=0; // start index of every block
while(cur){
if(i>=start and i<start+cur->num_char){ // half open BUG
// BUG
if(cur->num_char==5){ // node is full
node* nn=new node();
nn->v[0]=cur->v[4]; ////BUG
nn->num_char=1;
nn->next=cur->next, cur->next=nn;
for(int j=4;j>i-start;j--) cur->v[j]=cur->v[j-1];
cur->v[i-start]=ch;
}else{ // spacious
// right shift char in [i-start, cur->num_char-1]
for(int j=cur->num_char-1;j>i-start;j--) cur->v[j] = cur->v[j-1];
cur->v[i-start]=ch;
cur->num_char++;
}
num_char++;
return true;
}else{
start+=cur->num_char; // index + current block length = index of next block
}
cur=cur->next;
} //at this point, cur must be null now
//这里又分两种情况,一种是head is null, another case is all node are full
//BUG
node* n=new node();
n->num_char=1, num_char++;
n->v[0]=ch;
if(!head) head=n;
else{ // find the last full node
auto tail=head;
while(tail->next) tail=tail->next;
tail->next=n;
}
return true;
}
//类似insert,先考虑清楚delete的情况
//1.普通的去掉一个node里面的点.2.去掉node之后,这个点空了,那就把点删掉.
//也要考虑每个node里面长度的变化.
bool del(int i){
if(i<0 or i>=num_char) return false;
node d;
d.next=head;
node* c=head, *prev=&d;
prev->next=c;
int start=0;
while(c){
if(start<=i and i<start+c->num_char){ // BUG
if(c->num_char==1){
prev->next= c->next;
}else{
// left shift chars [i+1-start, c->num_char-1]
for(int j=i-start+1;j<c->num_char;j++) c->v[j];
}
c->num_char--, num_char--;
break;
}
start+=c->num_char;
c=c->next, prev=prev->next;
}
head = d.next; // old head could be removed!
}
};
void test(){
unrolledLL u;
for (int i = 0; i < 38; ++i) {
u.insert(char('a'+i%26), i);
}
assert(u.get(-1)==0);
assert(u.get(26)=='a');
u.del(25);
assert(u.get(25)=='a');
}
};
#endif //APPLECPP_UNROLLEDLL_H68.2 Roll Dice
扔N次就有6^N种不同的组合,虽然这些组合中一定有sum相同的. 总的个数一定是6^N. 然后要求这些路径中和为target的路径的个数X. 那么结果就是X/N.
这样就变成了求Permutation sum的问题.
Algo 1 - Naive
public double getPossibility(int roll_num, int target){
if (roll_num <= 0 || target < roll_num || target > 6 * roll_num) { return 0.0; }
int total = (int) Math.pow(6, roll_num);
int[] record = new int[1];
dfs(roll_num, target, record);
int count = record[0];
return (double)count/total;
}
public void dfs(int roll_num, int target, int[] record){
if (roll_num == 0 && target == 0){ record[0]++; return; }
if (roll_num <= 0 || target <= 0){ return; }
for (int i = 1; i <= 6; i++){ dfs(roll_num-1, target-i, record); }
return;
}Algo 2 - DFS Memo
//记忆化搜索解法,复杂度一定比DP要低,就是低到哪里去不太好计算.
//复杂度是 O(状态的个数*状态转移的复杂度),是O(6 * roll_num),因为每次只向下查6个.
//anyway,这个是最优解.面试时候直接给这个就行吧.
public double getPossibility_memo(int roll_num, int target){
if (roll_num <= 0 || target < roll_num || target > 6*roll_num) { return 0.0; }
int total = (int) Math.pow(6, roll_num); //这里注意一下,pow的返回类型是double
int[][] memo = new int[roll_num+1][target+1];
int count = dfsMemo(roll_num, target, memo);
return (double)count/total;
}
public int dfsMemo(int roll_num, int target, int[][] memo){
if (roll_num == 0){ if (target == 0) return 1; }
if (target > roll_num * 6 || target < roll_num){ return 0; }
if (memo[roll_num][target] != 0){ return memo[roll_num][target]; }
int res = 0;
for (int i = 1; i <= 6; i++)
res += dfsMemo(roll_num-1, target - i, memo);
memo[roll_num][target] = res; //这一步是更新记忆矩阵
return res;
}Algo 3 - DP
dp[i][j] - 扔i次和为j的路径数 等于 扔i-1次和为j-[1|2|3|4|5|6]的路径数的和.
如果i<j, dp[i][j]肯定为0,因为dice点数至少为1点,所以roll i次,和一定大于等于i. 这是一个upper triangular matrix.
int[roll_num+1][target+1]要加1是因为java的array的index是0-based的.
//dp写法,其实下一次扔出某个数字就是上次的结果加上1到6,所以每次向前查6个求和就可以了.
//复杂度也不低,应该是O(roll_num*target),如果target很大,就不太好了.
public double getPossibility_dp(int roll_num, int target){
if (roll_num <= 0 || target < roll_num || target > 6*roll_num) { return 0.0; }
int total = (int) Math.pow(6, roll_num);
int[][] dp = new int[roll_num+1][target+1]; //套个0比较方便
for (int j = 1; j <= 6; j++){ dp[1][j] = 1; } // base case
for (int i = 2; i <= roll_num; i++){
for (int j = i; j <= target; j++){ //每次向前查最多6个.
for (int k = 1; k <= 6 && j-k >= i-1; k++){
dp[i][j] += dp[i-1][j-k];
}
}
}
int count = dp[roll_num][target];
return (double)count/total;
}68.3 Git Commit
Given a git commit (wiki:…), each commit has an id. Find all the commits that we have.
class GitNode{
int id;
List<GitNode> parents;
public GitNode(int id){
this.id = id;
this.parents = new ArrayList<>();
}
}
public class Git_Commit {
//其实是找到了所有的parents,所以假设拿到的是最新的gitNode
//只有这种难度,才能大部分人都秒做吧.
public List<GitNode> findAllCommits(GitNode node){
List<GitNode> res = new ArrayList<>();
Queue<GitNode> queue = new LinkedList<>();
Set<GitNode> visited = new HashSet<>(); //去重
queue.offer(node);
visited.add(node);
while (!queue.isEmpty()){
GitNode cur = queue.poll();
res.add(cur);
for (GitNode par: cur.parents){
if (!visited.contains(par)){
queue.offer(par);
visited.add(par);
}
}
}
return res;
}
}- Follow Up
找到两个commit的最近公共parent commit.而且被要求优化,因为是follow up,所以到时候时间肯定 剩下不多,面试时候要直接出最优解.
public GitNode findLCA(GitNode node1, GitNode node2){
if (node1 == null || node2 == null) return null;
Queue<GitNode> q1 = new LinkedList<>();
q1.offer(node1);
Queue<GitNode> q2 = new LinkedList<>();
q2.offer(node2);
Set<GitNode> s1 = new HashSet<>();
Set<GitNode> s2 = new HashSet<>();
s1.add(node1);
s2.add(node2);
// int len1 = 1, len2 = 1; //万一是要求最短路径长度呢.
//while里面是&&,因为一旦其中一个终结那也不用搜了.
while (!q1.isEmpty() && !q2.isEmpty()){
//每个BFS都是一层一层的扫
int size1 = q1.size();
while (size1-- > 0){
GitNode cur1 = q1.poll();
for (GitNode par1 : cur1.parents) {
if (s2.contains(par1)){
return par1;
}
if (!s1.contains(par1)){
q1.offer(par1);
s1.add(par1);
}
}
}
int size2 = q2.size();
while (size2-- > 0){
GitNode cur2 = q2.poll();
for (GitNode par2 : cur2.parents) {
if (s1.contains(par2)){
return par2;
}
if (!s2.contains(par2)){
q2.offer(par2);
s2.add(par2);
}
}
}
}
return null;
} public static void main(String[] args) {
Git_Commit test = new Git_Commit();
/*
*
* 5 <- 4 <- 2
* \ \
* \ <- 3 <- 1
* */
GitNode g1 = new GitNode(1);
GitNode g2 = new GitNode(2);
GitNode g3 = new GitNode(3);
GitNode g4 = new GitNode(4);
GitNode g5 = new GitNode(5);
g1.parents.add(g3);
g1.parents.add(g4);
g2.parents.add(g4);
g3.parents.add(g5);
g4.parents.add(g5);
GitNode res = test.findLCA(g2, g3);
System.out.println(res.id);
}题目内容:
给出一个Git的commit,找出所有的parents.每个节点都有一个或多个parent. 另外每个commit都是带着ID的.就是没太懂它是输出所有的commit还是要求逐层打印. 第二题就是找到两个commit的公共祖先. Git的commit是可以分叉的也可以合并,所以这题其实是个图. 想来真是好久没弄github了. 其实就是BFS和双向BFS,注意好对复杂度的分析吧.优化就是双向BFS吧.
68.4 Normalized Title
Given a rawTitle, and a list(or array) of clean titles. For each clean title, the raw title can get a “match point”. For example, if raw title is “senior software engineer” and clean titles are “software engineer” and “mechanical engineer”, the “match point” will be 2 and 1. In this case we return “software engineer” because it has higher “match point”.
public class Normalized_Title {
public String getHighestTitle(String rawTitle, String[] cleanTitles){
String res = "";
int highScore = 0;
for (String ct : cleanTitles){
int curScore = getScore(rawTitle, ct);
if (curScore > highScore){
highScore = curScore;
res = ct;
}
}
return res;
}
//思路非常简单,两个title分别去查一下就行了.
//这个下面有问题,比如a b c和d c的例子,那只能开二维矩阵去搜最高分.
//不考虑顺序的话,就用map来记录词和位置吧.(而且它说没有重复的词,也是暗示用map)
public int getScore(String raw, String ct){
int s = 0, temp = 0;
int rIdx = 0, cIdx = 0;
String[] rA = raw.split(" ");
String[] cA = ct.split(" ");
while (rIdx < rA.length){
String rCur = rA[rIdx];
String cCur = cA[cIdx];
if (!rCur.equals(cCur)){
cIdx = 0;
temp = 0;
}
else {
temp++;
cIdx++;
}
rIdx++;
s = Math.max(s, temp);
if (cIdx == cA.length) break;
}
return s;
}
public static void main(String[] args) {
Normalized_Title test = new Normalized_Title();
String rawTitle = "senior software engineer";
String[] cleanTitles = {
"software engineer",
"mechanical engineer",
"senior software engineer"};
String result = test.getHighestTitle(rawTitle, cleanTitles);
System.out.println(result);
}
}