Chapter 20 Graph

20.1 Representation of Graph

20.1.1 1. Adjacency Matrix

vector<vector<int>> G; and G is always a square matrix.

20.1.4 4. Logical Graph

Sometimes very obvious like matrix, triangle; sometimes determined by rules like factor trees, Remove Invalid Parentheses.

Sometimes, algorithm has special requirements for graph representation.

hashtable还可以用来表示trie.

20.2 Graph Valid Tree

Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to check whether these edges make up a valid tree.

For example:

Given n = 5 and edges = [[0, 1], [0, 2], [0, 3], [1, 4]], return true.

Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [1, 3], [1, 4]], return false.

Show Hint

Note: you can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

https://www.lintcode.com/en/problem/graph-valid-tree/
https://leetcode.com/problems/graph-valid-tree/

http://www.cnblogs.com/grandyang/p/5257919.html

这道题给了我们一个无向图,让我们来判断其是否为一棵树,我们知道如果是树的话,所有的节点必须是连接的,也就是说必须是连通图,而且不能有环,所以我们的焦点就变成了验证是否是连通图和是否含有环.

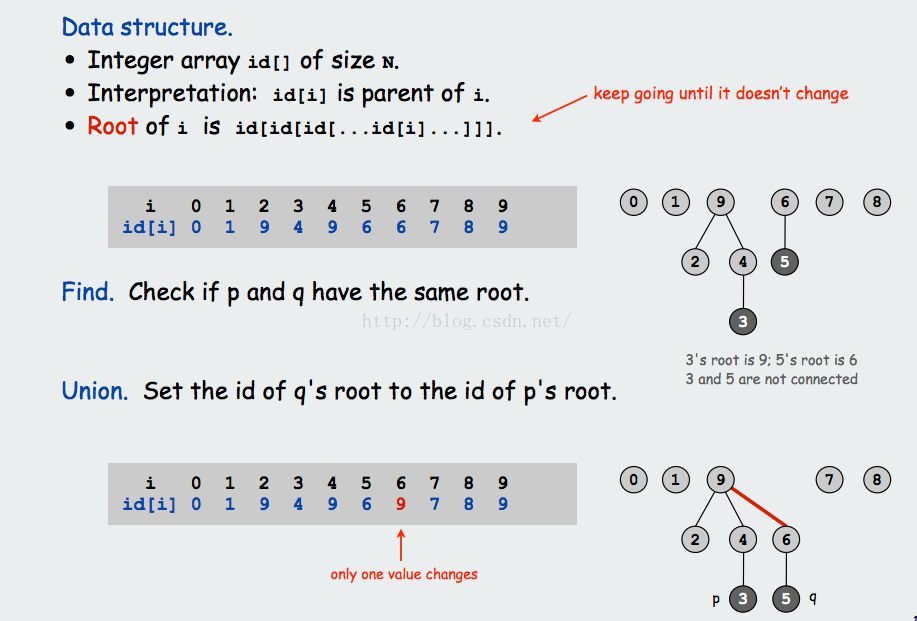
Union Find的方法,这种方法对于解决连通图的问题很有效,思想是我们遍历节点,如果两个节点相连,我们将其boss值连上,这样可以帮助我们找到环,我们初始化boss数组为-1,然后对于一个pair的两个节点分别调用find函数,得到的值 如果相同的话,则说明环存在 ,返回false,不同的话,我们将其roots值union上.

If two nodes have same boss before merge, there is a cycle.

如果没有告诉Vertex number n, the only input is edges, we need to count it using a set.

这道题告诉我们如何用union find判断是否有环.

类似: graph.html#number-of-connected-components-in-an-undirected-graph

20.2.1 Java

  • DFS
  • BFS

20.3 BFS (Single/Double/Multiple Sources)

BFS is normally implemented in a iterative way, but it can be done in recursive way too! (see Word Ladder II)

In iterative BFS, queue is the core data structure. In recursive BFS,….

MSBFS paper

20.4 Walls and Gates (MS-BFS)

You are given a m x n 2D grid initialized with these three possible values.

-1  - A wall or an obstacle.
0   - A gate.
INF - Infinity means an empty room.
      We use the value 2^{31} - 1 = 2147483647 to represent INF as 
      you may assume that the distance to a gate is less than 2147483647.

Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.

For example, given the 2D grid:

INF  -1  0  INF
INF INF INF  -1
INF  -1 INF  -1
  0  -1 INF INF

After running your function, the 2D grid should be:

  3  -1   0   1
  2   2   1  -1
  1  -1   2  -1
  0  -1   3   4

This is pretty much like BBFS(bi-directional BFS).(Page 109 CC189.) Actually it is the simplest version of multi-source-BFS problem.

http://leetcode.com/problems/walls-and-gates/

Here is how to initialize an STL array?

  • C++
  • Java

Three ways to traverse a matrix: Double for loop, BFS, DFS.

20.5 127. Word Ladder

Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:

Only one letter can be changed at a time.
Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

For example,

Given:
beginWord = “hit”
endWord = “cog”
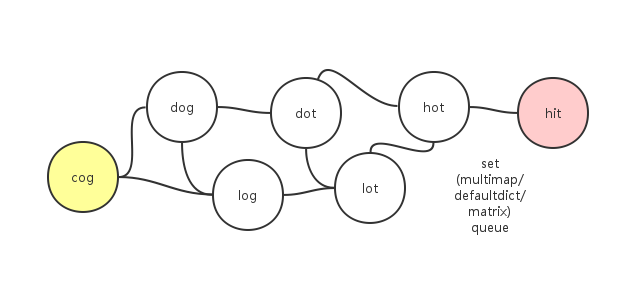
wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]

As one shortest transformation is “hit” -> “hot” -> “dot” -> “dog” -> “cog”, return its length 5.

Note:

Return 0 if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.
You may assume no duplicates in the word list.
You may assume beginWord and endWord are non-empty and are not the same.

https://leetcode.com/problems/word-ladder/

http://bangbingsyb.blogspot.com/2014/11/leetcode-word-ladder-i-ii.html

When using map to represent an (un)directed graph, you need to call \(insert()\) twice!!

Recently, leetcode changed the signature of the function.

20.5.1 BFS

传统的老实方法. leetcode的旧的signature(unordered_set<string>& wordList),注意当word数量N大于52=2x26个的时候strategy 2要快些.

2017年之后leetcode改动了函数的signature, 程序accordingly becomes to the following:

20.5.3 Bi-Directional BFS

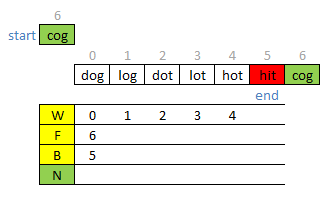
这是本题的最优解.To use two hash tables to build paths from beginWord and endWord relatively.

改了signature之后的版本1:

改了signature之后的版本2, 找neighbour的方法不同:

不同:1. 用int代表vector里面的string, 2. loop vector to find negihbours

20.6 433. Minimum Genetic Mutation

A gene string can be represented by an 8-character long string, with choices from “A”, “C”, “G”, “T”.

Suppose we need to investigate about a mutation (mutation from “start” to “end”), where ONE mutation is defined as ONE single character changed in the gene string.

For example, “AACCGGTT” -> “AACCGGTA” is 1 mutation.

Also, there is a given gene “bank”, which records all the valid gene mutations. A gene must be in the bank to make it a valid gene string.

Now, given 3 things - start, end, bank, your task is to determine what is the minimum number of mutations needed to mutate from “start” to “end”. If there is no such a mutation, return -1.

Note:

Starting point is assumed to be valid, so it might not be included in the bank.
If multiple mutations are needed, all mutations during in the sequence must be valid.
You may assume start and end string is not the same.
Example 1:

start: "AACCGGTT"
end:   "AACCGGTA"
bank: ["AACCGGTA"]

return: 1

Example 2:

start: "AACCGGTT"
end:   "AAACGGTA"
bank: ["AACCGGTA", "AACCGCTA", "AAACGGTA"]

return: 2

Example 3:

start: "AAAAACCC"
end:   "AACCCCCC"
bank: ["AAAACCCC", "AAACCCCC", "AACCCCCC"]

return: 3

https://leetcode.com/problems/minimum-genetic-mutation/

20.7 126. Word Ladder II

Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

  1. Only one letter can be changed at a time
  2. Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

For example, Given:
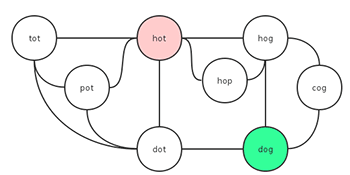
beginWord = “hit”
endWord = “cog”
wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]

Return

[
[“hit”,“hot”,“dot”,“dog”,“cog”],
[“hit”,“hot”,“lot”,“log”,“cog”]
]

Note:

Return an empty list if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.
You may assume no duplicates in the word list.
You may assume beginWord and endWord are non-empty and are not the same.

UPDATE (2017/1/20):
The wordList parameter had been changed to a list of strings (instead of a set of strings). Please reload the code definition to get the latest changes.

https://leetcode.com/problems/word-ladder-ii/

// Runtime: 688 ms
struct Solution {
  unordered_map<string, unordered_set<string>> G;//1. Graph
  unordered_map<string, unordered_set<string>> P;//2. Path

  void make_graph(const unordered_set<string>& wordList) { //3. O(26*N*L)
    for (const string& t : wordList) { // N
      string s;
      for (int i = 0; i<t.size(); ++i) // L
        for (s = t, s[i] = 'a'; s[i] <= 'z'; ++s[i]) // 26
          if (s != t && wordList.count(s))
            G[t].insert(s), G[s].insert(t);
    }
  }

  using VVS = vector<vector<string>>;
  VVS findLadders(string beginWord, string endWord, unordered_set<string> &wordList) {
    make_graph(wordList);
    queue<pair<string, int>> Q; // 4. BFS
    unordered_set<string> V, N;// 5. visited and next layer visited
    Q.push({ beginWord,1 }), V.insert(beginWord);
    int last = -1, curlevel = 1;
    while (!Q.empty()) { // 6. BFS
      auto t = Q.front(); Q.pop();
      // add all nodes in current last, nodes must point to NEXT layer!
      if (curlevel != t.second)// 7. At the beginning of a new layer
        curlevel = t.second, V.insert(N.begin(), N.end()), N.clear();
      if (t.first == endWord)
        last = t.second;
      else {
        if (last>0 && last <= t.second) continue;// 8. optimization
        for (const string& s : G[t.first]) {// neighbours
          if (V.count(s) == 0) { // 9. cannot be previous layers' nodes
            if (N.count(s) == 0) // 10. shouldn't push duplicates into Q
              Q.push({ s, t.second + 1 }), N.insert(s);
            P[t.first].insert(s);// 11. Record paths
          }
        }
      }
    }
    VVS r;
    if (last<0) return r;// 12. no valid path
    vector<string> p;
    p.reserve(last), p.push_back(beginWord);
    dfs(beginWord, endWord, r, p, last, 1);// 13. DFS to find paths
    return r;
  }

  void dfs(string cur, string& endWord, VVS& r, vector<string>& p, int last, int l) {
    if (last == l) {
      if (cur == endWord) r.push_back(p);
      return;
    }
    for (auto s : P[cur]) {
      if (find(p.begin(), p.end(), s) == p.end()) {// 14. no duplicate nodes in path
        p.push_back(s);
        dfs(s, endWord, r, p, last, l + 1);
        p.pop_back(); // backtrack
      }
    }
  }
};

20.7.1 Optmization

  • \(make\_graph(.)\) is unnecessary. Imagine beginWord and endWord are negihbours in a huge graph. This speeds up the program a lot!
  • Layer Marker with a Dummy Node

Here we use a dummy node(empty string) to mark the end of a layer. This won’t speed up the program a lot, but it saves more space, and makes code more concise.

  • Visited Set
  • Double Source BFS

Walls and Gates is a multi-srouce BFS problem. Here we can use bouble-source BFS to optimize our program.

注意BFS返回bool.

http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=213577

见过不少面经提到被问到1.5版本,就是只输出一条最短路径,同时还被challenge用26个字符iteration太慢,想问问大家怎么回答这个follow up 的?

如果只需要find one shortest path, 那么就比较简单了这里:

20.8 Number of Connected Components in an Undirected Graph

Given n nodes labeled from 0 to n - 1 and a list of undirected edges (each edge is a pair of nodes), write a function to find the number of connected components in an undirected graph.

Example 1:

 0          3
 |          |
 1 --- 2    4

Given n = 5 and edges = [[0, 1], [1, 2], [3, 4]], return 2.

Example 2:

 0           4
 |           |
 1 --- 2 --- 3

Given n = 5 and edges = [[0, 1], [1, 2], [2, 3], [3, 4]], return 1.

Note:
You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

https://leetcode.com/problems/number-of-connected-components-in-an-undirected-graph

http://buttercola.blogspot.com/2016/01/leetcode-number-of-connected-components.html

https://asanchina.wordpress.com/2015/12/29/323-number-of-connected-components-in-an-undirected-graph/

为什么叫动态联通(Dynamic Connectivity),因为merge的过程就是把小图联通成大图的过程.

小知识点:
1. http://stackoverflow.com/questions/15292892/what-is-return-type-of-assignment-operator
2. greater是一个binary operator,用在这里的话必须用bind:

关于复杂度, 参考阅读: http://www.cnblogs.com/SeaSky0606/p/4752941.html

20.9 684. Redundant Connection

We are given a “tree” in the form of a 2D-array, with distinct values for each node.

In the given 2D-array, each element pair [u, v] represents that v is a child of u in the tree.

We can remove exactly one redundant pair in this “tree” to make the result a tree.

You need to find and output such a pair. If there are multiple answers for this question, output the one appearing last in the 2D-array. There is always at least one answer.

Example 1:
Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: Original tree will be like this:

  1
 / \
2 - 3

Example 2:
Input: [[1,2], [1,3], [3,1]]
Output: [3,1]
Explanation: Original tree will be like this:

  1
 / \\
2   3

Note:
The size of the input 2D-array will be between 1 and 1000.
Every integer represented in the 2D-array will be between 1 and 2000.

https://leetcode.com/problems/redundant-connection/

Algo: Union find

  • JAVA

20.10 Shortest Path

CLRS P678

20.12 Expression Add Operators (DFS + Pruning)

Given a string that contains only digits 0-9 and a target value, return all possibilities to add binary operators (not unary) +, -, or * between the digits so they evaluate to the target value.

Examples:

"123", 6 -> ["1+2+3", "1*2*3"] 
"232", 8 -> ["2*3+2", "2+3*2"]
"105", 5 -> ["1*0+5","10-5"]
"00", 0 -> ["0+0", "0-0", "0*0"]
"3456237490", 9191 -> []

https://leetcode.com/problems/expression-add-operators/

Based on subsets but the algo is even more complicated.

  1. In the for loop of subsets, there is only one recursive call. But in this problem, there are three.

  2. Pruning: if (cur.size() > 1 && cur[0] == '0') return;

  3. Considering 1+2*3, we need to save previous value to the stack as d. The dfs for multiplication is: dfs(n, target, d*t, (c-d)+d*t, p+"*"+cur, res);

http://www.cnblogs.com/grandyang/p/4814506.html

20.13 Route Tracking

If you want to track the routes, you have to add more stuff in the stack: final_result, partial_solution etc

https://leetcode.com/problems/word-search/ https://leetcode.com/problems/letter-combinations-of-a-phone-number/

20.14 Kangroo Jump

There are two types of kangroos, left learning(<) and right learning(>) ones. Six kangroos are initially arranged on seven slots in the following configration:
[>,>,>,_,<,<,<]
The empty slot is indicated by ’_’ and the task is to move all the kangaroos on the left to the right and all the kangroos on the right to the left, as in:
[<,<,<,_,>,>,>]
The rules are simple:
1. a right leaning kangaroo can only move to the right, left kangroo only left 2. a kangroo can either move one step forward to fill an empty slot or jump over any one kangroo to occupy an empty slot.

Is it possible to perform a sequence of moves to solve the task above?

General speaking, there are 4 possible next steps for any current position, we can use DFS to search path and pruning to speed up.

这道题的难点在于如何pruning.

不失一般性,假设第一步是>>>_><<<<,第二步必然是>>><>_<<<,不可能是>>_>><<<<,否则右边会出现>><,这种形状必然无解.

从第二步>>><>_<<<下一步必然是>>><><_<<,不可能是>>>><_><<<,否则会出现><_><,这种形状也必然无解.也不可能是>>><><<_<,否则左边是><<,必然无解.

><_><的下一步是_<>><或者><<>_.

再往后原因类似,反正每一步可行的决策都是唯一的

其实上面的Pruning并没有剪掉所有的烂枝桠.看下图,上面的逻辑漏掉了情况E.

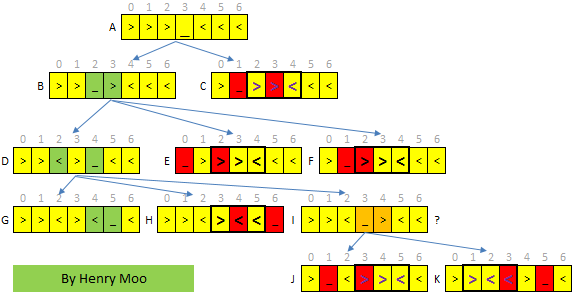
:Explorer:(506256462) 3:28:49 AM
但是对于形如>>>_<<<的数据来说,这个剪枝用不上
:Explorer:(506256462) 4:11:26 AM
有了>><和><<就不用加><_><了
:Explorer:(506256462) 4:11:47 AM
我之前说错了,不只是>>>_<<<,其实在任何数据里,都用不上><_><
:Explorer:(506256462) 4:12:09 AM
我在证明里考虑><_><只是因为可以简化后续证明

所以正确的Pruning是下面这样的:

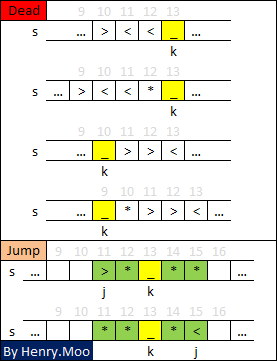
代码实现:

运行结果:

$ulimit -s unlimited
$time ./kangroo_g 8000
path found

real    0m3.772s
user    0m3.144s
sys     0m0.636s

这道题告诉我们,正确的Pruning实在是太重要了.

看看复杂度:

$time ./kangroo_g 10240
path found
real    0m6.183s
user    0m5.208s
sys     0m0.976s
$time ./kangroo_g 5120
path found
real    0m1.574s
user    0m1.284s
sys     0m0.276s
$time ./kangroo_g 2560
path found
real    0m0.411s
user    0m0.336s
sys     0m0.072s
$time ./kangroo_g 1280
path found
real    0m0.112s
user    0m0.088s
sys     0m0.020s
$time ./kangroo_g 640
path found
real    0m0.036s
user    0m0.028s
sys     0m0.004s
$time ./kangroo_g 320
path found
real    0m0.012s
user    0m0.008s
sys     0m0.000s
$time ./kangroo_g 160
path found
real    0m0.011s
user    0m0.008s
sys     0m0.000s

数据量是原来2倍的时候,时间是原来的4倍.数据量太小的时候,算法不占主因,看不出来.一边袋鼠300只以上就可以看得出来了.

复杂度: T:\(O(N^2)\), S:\(O(N^2)\)

到达目标的步数是单边袋鼠数量+1的平方.

Ocaml Code:

20.15 Topological Sort

http://blog.csdn.net/dm_vincent/article/details/7714519

Concept: degree, in-degree, out-degree

  1. Kahn’s Algorithm (BFS)
    The advantage of Kahn’ algo is DAG checking is not need.

  2. DFS

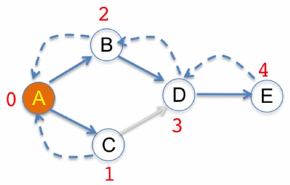
DAG checking must be done or the DFS will go into a infinite loop.

T: \(O(|V| + |E|)\), S: \(O(|E|)\)

20.16 Course Schedule - Khan BFS(1 set+2 maps)

There are a total of n courses you have to take, labeled from 0 to n - 1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

For example:

2, [[1,0]]

There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.

2, [[1,0],[0,1]]

There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

https://leetcode.com/problems/course-schedule/

http://www.cnblogs.com/grandyang/p/4484571.html
https://en.wikipedia.org/wiki/Topological_sorting#Kahn.27s_algorithm
(CLRS p615. 22.4-3)

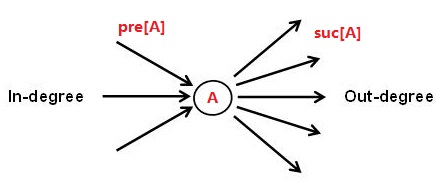
topologically sortable == No cycle!

下面用一个例子在解释Khan’s Algorithm. Example:

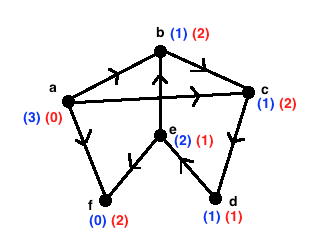
pre[b]=a,e
pre[c]=a,b
pre[d]=c
pre[e]=d
pre[f]=e,a

suc[a]=b,c,f
suc[b]=c
suc[c]=d
suc[d]=e
suc[e]=b,f

ns=a,b,c,d,e,f //all nodes in the graph
    1. 找到0-indegree node: 把pre的key从ns里面删除,ns==[a],里面包含的就是0-indegree nodes(‘a’ in this case).
    1. 然后从pre和suc里面移除所有a节点: 首先检查suc,找suc[a]里面的点b,c,f,然后找pre[b], pre[c], pre[f],里面肯定都包含有a,把这个a删除,如果剩下为空set,说明又找到一个0-indegree node.
    1. 如此循环,直到ns为空!
    1. 最后看pre和suc也为空的话,说明是topologically sortable!!!

在这个过程中已经按顺序找到了所有的node,in another words, we have done topological sort.

After removing ‘a’, it becomes:

pre[b]=e
pre[c]=b
pre[d]=c
pre[e]=d
pre[f]=e

suc[b]=c
suc[c]=d
suc[d]=e
suc[e]=b,f

ns=[] // 0-indegree nodes

这个ns已经为空了,而pre和suc还不为空,说明不可sort. 的确, b-c-d-e是一个cycle.

下面的参数prerequisites是pre的vector的表示方式. 注意这种表示有向图的方式.

  • C++

这题最好画图说明,算法其实简单但是很绕.

  • Java

BFS:

DFS:

20.17 Course Schedule II

There are a total of n courses you have to take, labeled from 0 to n - 1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses.

https://leetcode.com/problems/course-schedule-ii/

(CLRS p615. 22.4-5) 这道题根据pre求DAG里面节点的order. 采用和BFS类似的思想,一层层往里面剥.剥掉一层之后里面紧挨一层的indgree数目就减1.

这道题也是用khan algorithm,这里的G相当于suc, pre就是pre不过表现形式不一样而已.这里也用了queue,而不是set.

这道题变化一下可以考察求出所有可行的课程安排:

然后再用Combinatorics DFS的方法求出所有的schedule, like combinatorics.html#letter-combinations-of-a-phone-number-1.

  • Java

20.18 332. Reconstruct Itinerary

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary [“JFK”, “LGA”] has a smaller lexical order than [“JFK”, “LGB”].
All airports are represented by three capital letters (IATA code).
You may assume all tickets form at least one valid itinerary.

Example 1:

tickets = [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Return ["JFK", "MUC", "LHR", "SFO", "SJC"].

Example 2:

tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Return ["JFK","ATL","JFK","SFO","ATL","SFO"].

Another possible reconstruction is [“JFK”,“SFO”,“ATL”,“JFK”,“ATL”,“SFO”]. But it is larger in lexical order.

https://leetcode.com/problems/reconstruct-itinerary/

Note there may be more than one same tickets. For example:

[['ANU', 'EZE'], ['ANU', 'JFK'], ['ANU', 'TIA'], ['AXA', 'TIA'], 
['EZE', 'AXA'], ['JFK', 'ANU'], ['JFK', 'TIA'], ['TIA', 'ANU'], 
['TIA', 'ANU'], ['TIA', 'JFK']]

由于题目中限定了一定会有解,那么等图中所有的multiset中都没有节点的时候,我们把当前节点存入结果中

这道题的本质是计算一个最“小”的欧拉路径(Eulerian path).对于一个节点（当然先从JFK开始),贪心地访问最小的邻居,访问过的边全部删除.当碰到死路的时候就回溯到最近一个还有出路的节点,然后把回溯的路径放到最后去访问,这个过程和后序遍历的一样.1. 如果子节点没有死路（每个节点都只左子树),前序遍历便是欧拉路径.2. 如果子节点1是死路,子节点2完成了遍历,那么子节点2先要被访问.1,2都和后序遍历的顺序正好相反.?

20.20 310. Minimum Height Trees

For a undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.

Format:
The graph contains n nodes which are labeled from 0 to n - 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).
You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.

Example 1: Given n = 4, edges = [[1, 0], [1, 2], [1, 3]], return [1].

        0
        |
        1
       / \
      2   3

Example 2: Given n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]], return [3, 4].

     0  1  2
      \ | /
        3
        |
        4
        |
        5

https://leetcode.com/problems/minimum-height-trees

这道题与前面不同的是它不是一个DAG,是undirected graph.而且它是树,所以没有环! 所以采用Khan Algo的思想就是剥洋葱! 但是剥到什么时候为止呢? 因为没有环,所以到只剩2个或者1个node的时候结束. 还有如何确定最外层的leaf node呢?上面的方法是找in-degree,那是DAG的用法.对本题的无向树来说,邻居的数目(degree)是1表示是leaf node!

这道题的实现involves到C++中如何在循环中从STL container删除元素. bug多发地段之一.
http://en.cppreference.com/w/cpp/container/set/erase
http://en.cppreference.com/w/cpp/container/unordered_set/erase

auto it=ms.begin();
while(it!=ms.end())
  if(xxx)
    it=ms.erase(it);
  else it++;

此外本题的map和set都可以改为unordered版本的. Easy,略.

20.21 Conclusion

The template for DFS:

dfs(r, p, graph, x)

where

r is refernce of full solution, which you want to return finally.

p is partial solution, which is element in r.

graph is graph you want to traverse.

x is used for termination condition of dfs.

20.22 399. Evaluate Division

https://leetcode.com/problems/evaluate-division/

https://en.wikipedia.org/wiki/Floyd%E2%80%93Warshall_algorithm

https://discuss.leetcode.com/topic/58482/9-lines-floyd-warshall-in-python

http://bookshadow.com/weblog/2016/09/11/leetcode-evaluate-division/

https://discuss.leetcode.com/topic/58577/0ms-c-java-union-find-solution

https://www.youtube.com/watch?v=LwJdNfdLF9s

http://massivealgorithms.blogspot.com/2016/09/leetcode-399-evaluate-division.html

这个是一个边有weight的图,与前面的都不同.

http://xiadong.info/2016/09/leetcode-399-evaluate-division/ (构建邻接矩阵)

struct Solution {
  // 由于对于string的比较等操作很费时, 所以用一个map把string与int对应起来.
  unordered_map<string, int> nodes;
  vector<double> calcEquation(vector<pair<string, string>> equations,
    vector<double>& values, vector<pair<string, string>> queries) {
    for (int i = 0; i < equations.size(); i++) {
      // 给每一个string分配一个下标
      // 注意这里有个隐藏bug, 假如map/unordered_map对象m中不包含a,
      // 那么在使用m[a]时实际上是已经创建一个a的key和对应的value, 导致size加1
      // 所以如果我们想让第n个加入的元素的value为n-1的话,
      // 需要赋值m.size() - 1而不是m.size()
      if (!nodes.count(equations[i].first)) {
        nodes[equations[i].first] = nodes.size() - 1;
      }
      if (!nodes.count(equations[i].second)) {
        nodes[equations[i].second] = nodes.size() - 1;
      }
    }
    vector<vector<double>> g(nodes.size(), vector<double>(nodes.size(), -1.0));
    for (int i = 0; i < equations.size(); i++) {
      // 构建邻接矩阵
      g[getNode(equations[i].first)][getNode(equations[i].second)] = values[i];
      g[getNode(equations[i].second)][getNode(equations[i].first)] = 1 / values[i];
    }
    vector<double> ret(queries.size());
    for (int i = 0; i < queries.size(); i++) {
      string a = queries[i].first, b = queries[i].second;
      if (!nodes.count(a) || !nodes.count(b)) {
        // 如果出现了不存在的节点
        ret[i] = -1.0;
      } else {
        // 使用BFS来搜索路径
        ret[i] = BFS(g, getNode(a), getNode(b));
      }
    }
    return ret;
  }
  int getNode(string s) {
    return nodes[s];
  }
  double BFS(vector<vector<double>> &g, int a, int b) {
    // 如果是同一个节点就直接返回
    if (a == b) return 1.0;
    int n = g.size();
    vector<int> visited(n, 0); // 用于保存是否访问过节点
    queue<int> q; // BFS队列, 保存节点下标
    queue<double> v; // 用于保存从a到BFS队列中相应的节点的路径乘积
    q.push(a);
    visited[a] = 1;
    v.push(1.0);
    while (!q.empty()) {
      int node = q.front();
      double value = v.front();
      for (int i = 0; i < n; i++) {
        if (visited[i] || g[node][i] == -1.0) continue; // 节点i已经访问过或者没有边到达i
        visited[i] = 1;
        q.push(i);
        double len = value * g[node][i]; // 从a到i的路径权值乘积
                                         // 添加新的边
        g[a][i] = len;
        g[i][a] = 1 / len;
        if (i == b) { // 抵达b点
          return len;
        }
        v.push(len);
      }
      q.pop();
      v.pop();
    }
    return -1.0;
  }
};

http://www.cnblogs.com/grandyang/p/5880133.html

最专业的还是用Floyd to find transitive closure.

http://bookshadow.com/weblog/2016/09/11/leetcode-evaluate-division/

  • Transitive Closure

http://www.voidcn.com/blog/qq_33406883/article/p-6103528.html

http://blog.csdn.net/clearriver/article/details/4548314

http://www.ivy-end.com/archives/999

20.23 529. Minesweeper

https://leetcode.com/problems/minesweeper/#/description

对于当前需要点击的点,我们先判断是不是雷,是的话直接标记X返回即可.
如果不是的话,我们就数该点周围的雷个数,如果周围有雷,则当前点变为雷的个数并返回.(这条容易搞混.)
如果没有的话,把current cell标记为B,再对周围所有的点调用递归函数再点击即可.

refer: http://www.cnblogs.com/grandyang/p/6536694.html

20.24 317. Shortest Distance from All Buildings

You want to build a house on an empty land which reaches all buildings in the shortest amount of distance. You can only move up, down, left and right. You are given a 2D grid of values 0, 1 or 2, where:

  • Each 0 marks an empty land which you can pass by freely.
  • Each 1 marks a building which you cannot pass through.
  • Each 2 marks an obstacle which you cannot pass through.

For example, given three buildings at (0,0), (0,4), (2,2), and an obstacle at (0,2):

1 - 0 - 2 - 0 - 1
|   |   |   |   |
0 - 0 - 0 - 0 - 0
|   |   |   |   |
0 - 0 - 1 - 0 - 0

The point (1,2) is an ideal empty land to build a house, as the total travel distance of 3+3+1=7 is minimal. So return 7.

https://leetcode.com/problems/shortest-distance-from-all-buildings

一开始看就想到MultiSource BFS来做,不过implement起来很困难其实. 先来看看网络上大神的解法:

https://discuss.leetcode.com/topic/31702/36-ms-c-solution

https://goo.gl/6GRfLh

还有一个解法: http://bit.ly/2vejibH 72%

20.25 133. Clone Graph

Clone an undirected graph. Each node in the graph contains a label and a list of its neighbors.

OJ’s undirected graph serialization:

Nodes are labeled uniquely. We use # as a separator for each node, and , as a separator for node label and each neighbor of the node.

As an example, consider the serialized graph {0,1,2#1,2#2,2}.

The graph has a total of three nodes, and therefore contains three parts as separated by #.

1.First node is labeled as 0. Connect node 0 to both nodes 1 and 2.
2.Second node is labeled as 1. Connect node 1 to node 2.
3.Third node is labeled as 2. Connect node 2 to node 2 (itself), thus forming a self-cycle.

Visually, the graph looks like the following:

       1
      / \
     /   \
    0 --- 2
         / \
         \_/

https://leetcode.com/problems/clone-graph

解题思路

首先,要遍历无向图,需要使用Hash Map来当作visited数组,防止重复访问而造成程序中的死循环. 遍历图有两种方式 - BFS & DFS,本题均可采用.
BFS - 使用Queue (prefer)
DFS - 递归或者使用Stack,对于DFS,每次clone一个node的时候,就要把它所有的neighbor加入到新clone的node的neighbor中,此时recursivly调用dfs,如果没有visited过 - 新建一个node,否则直接从map中找到返回

在visited数组中,key值为原来的node,value为新clone的node,如果一个node不存在于map中,说明这个node还未被clone,将它clone后放入queue中继续处理neighbors

  • JAVA
  • Python

Check Copy list with random pointer

20.26 785. Is Graph Bipartite?

Given a graph, return true if and only if it is bipartite.

Recall that a graph is bipartite if we can split it’s set of nodes into two independent subsets A and B such that every edge in the graph has one node in A and another node in B.

The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice.

Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:

0----1
|    |
|    |
3----2

We can divide the vertices into two groups: {0, 2} and {1, 3}.

Example 2:
Input: [[1,2,3], [0,2], [0,1,3], [0,2]]
Output: false
Explanation:
The graph looks like this:

0----1
| \  |
|  \ |
3----2

We cannot find a way to divide the set of nodes into two independent ubsets.

https://leetcode.com/problems/is-graph-bipartite/

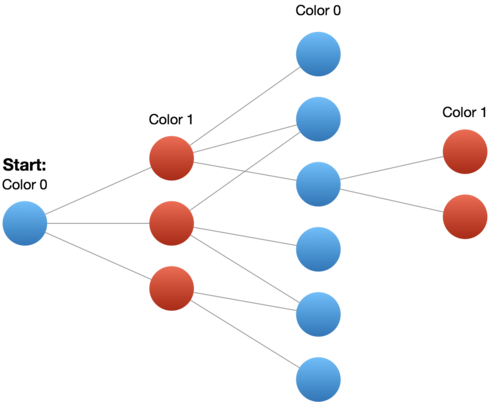
注意这下面的DFS,BFS都没有用到visited set,因为有了color array.

  • DFS

第16行也可以写成color[nei] = color[node] ^ 1;,实际上这里1可以换成任意整数.因为a^b=c中的三元素可以互相交换.

  • BFS

-1一直不停的乘以自身也可以产生这种alternate序列.

class Solution {
    public boolean isBipartite(int[][] graph) {
        int[] color = new int[graph.length];
        for(int k=0; k<graph.length; k++) { // the graph might be disconnected
            if(color[k]!=0) continue;
            Queue<Integer> q = new LinkedList<>();
            q.add(k);//start BFS
            int set = -1;
            while(!q.isEmpty()) {
                int size = q.size();
                set *= -1; //1,-1,1,-1... assign the set 1/-1 level by level
                while(size--==0) {
                    int v = q.poll();
                    if(color[v]!=0 && color[v]!=set) return false;
                    color[v] = set;
                    for(int child:graph[v]) {
                        if(color[child]==0)
                            q.offer(child);
                    }
                }
            }
        }
        return true;
    }
}

http://www.geeksforgeeks.org/bipartite-graph/
http://www.1point3acres.com/bbs/forum.php?mod=viewthread&tid=211298

二分图就是说这个图的vertex能分为两个部分,而所有edge都是从其中一个部分到另一个部分的.比如顶点{1, 2, 3, 4, 5}, 边{1->2, 1->3, 2->4, 2->5, 3->5},则顶点可分为{1, 4, 5} {2, 3}

这是图论里一个基本概念.常见的做法是染色法(实际上就是开一个hashtable做标记),从一个顶点开始,1染成红色,因为有1->2,1->3, 2和3都染成黑色,因为有2->4, 2->5, 4,5都染成红色,挺简单的,估计正常来说这个写完应该还有其他followup

http://code.geeksforgeeks.org/SBXB1X

20.27 Dijkstra Algorithm

https://www.youtube.com/watch?v=8Ls1RqHCOPw
https://www.hackerrank.com/challenges/dijkstrashortreach/problem

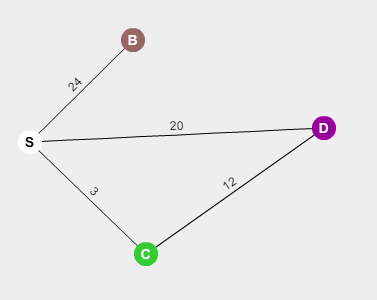
  • Dijkstra(BFS + PQ. Works without visited set)

from here: https://github.com/shadowwalker2718/Judge/blob/master/HackerRank/Dijkstra-%20Shortest%20Reach%202.cpp

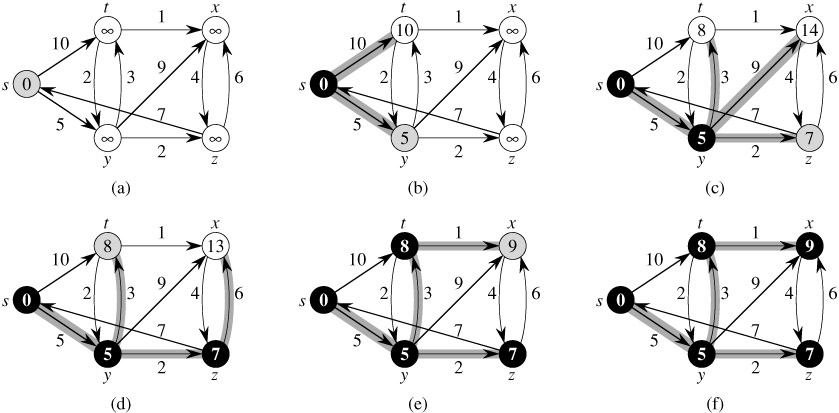
  • Dijkstra (BFS+PQ) in implicit Graph with a visited set

Removing the relax operation in line 38, it also works:

20.28 787. Cheapest Flights Within K Stops

There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.

Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1:

Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200

Explanation:
The graph looks like this:

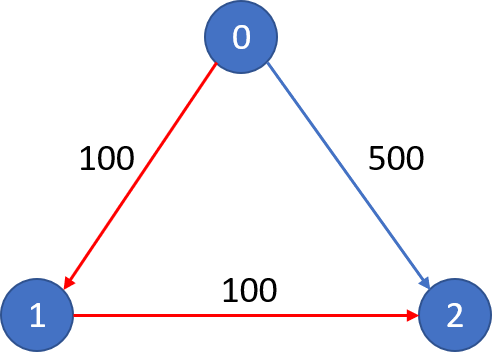
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500

Explanation:
The graph looks like this:

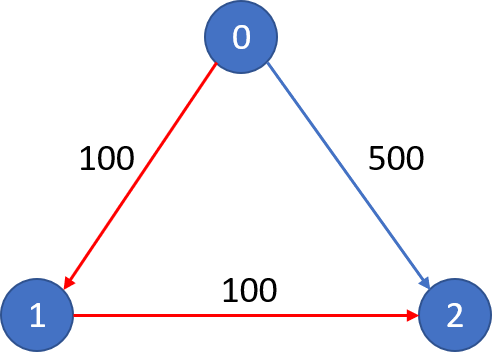
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

https://leetcode.com/problems/cheapest-flights-within-k-stops/

这个写法比较特殊:

  • JAVA